动态规划的原理
动态规划的思想与分治、递归都有些类似,为何我们要使用动态规划?
动态规划相比于递归,他不用重复计算子问题,他将已经解决过的问题存储下来,每个问题都可以划分为子问题求解。是一种空间换时间的手段
动态规划的步骤
我们知道了动态规划是利用历史记录来避免重复计算,因此我们一般用数组来保存记录(一维或者是二维)
- 明确记录的数组元素代表着什么
- 找出如何通过子问题的解求出父问题,也就是找出通项公式,比如斐波拉且数列中
dp[n] = dp[n-1] + dp[n-2] - 划定边界条件,手动填入最小子问题的解也就是初始值
- 选择计算顺序,分别是自顶向下和自底向上,前者需要记录下已经求出的值,遇到相同数据时直接读取;后者由初始值和递推公式求到所需的问题
动态规划的适用范围
- 计数:从左上角有多少种方法走到右下角,多少种方法使其k个数之和为Sum
- 求最大最小值:最长上升子序列长度,路径最大数字和
- 求存在性:能否选出k个数和为Sum,取石子游戏先手是否必胜
例题
背包问题
背包问题定义的理解:给定一个背包容量target,再给定一个数组nums(物品),能否按一定方式选取nums中的元素得到target
背包问题的类型
- **01背包问题:**每个元素最多取1次。具体来讲:一共有 N 件物品,第 i(i 从 1 开始)件物品的重量为 w[i],价值为 v[i]。在总重量不超过背包承载上限 V 的情况下,能够装入背包的最大价值是多少?
- **完全背包问题:**每个元素可以取多次。具体来讲:完全背包与 01 背包不同就是每种物品可以有无限多个:一共有 N 种物品,每种物品有无限多个,第 i(i 从 1 开始)种物品的重量为 w[i],价值为 v[i]。在总重量不超过背包承载上限 V 的情况下,能够装入背包的最大价值是多少?
- **分组背包问题:**有多个背包,需要对每个背包放入物品,每个背包的处理情况与完全背包完全相同。
解题模板
背包问题大体的解题模板是两层循环,分别遍历物品nums和背包容量target,然后写转移方程,根据背包的分类我们确定物品和容量遍历的先后顺序,根据问题的分类我们确定状态转移方程的写法。
1、0/1背包:外循环nums,内循环target,target倒序且target>=nums[i];
2、完全背包(组合):外循环nums,内循环target,target正序且target>=nums[i];
3、完全背包(排列):外循环target,内循环nums,target正序且target>=nums[i];
4、分组背包:这个比较特殊,需要多重循环:外循环nums,内部循环根据题目的要求构建多重背包循环
例题
一个只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
思路
01背包问题,这道题相当于找到一个子集,其和为 sum / 2,这个 sum / 2 就是 target(target 间接给出)。于是转化为是否可以用 nums 中的数组合和成 target。

给你一个字符串 s 和一个字符串列表
wordDict作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
思路
完全背包问题(排列),外层循环为 target ,内层循环为选择池 wordDict。
dp[i] 表示以 i 结尾的字符串是否可以被 wordDict 中组合而成。
- 外层遍历 s 中每一个与 word 同长度的字串
s.substring(i - wordLen, i) ; - 内层遍历 wordDict 每个 word。
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1
两个背包的01背包问题,计算出strs中每个值的0和1个数,然后用dp来计算
**注意:**在看到一道背包问题时,应该用搜索还是动态规划呢?
首先,可以从数据范围中得到命题人意图的线索。如果一个背包问题可以用动态规划解,**背包容量(V)一定不能很大,否则O(VN)的算法无法承受,而一般的搜索解法都是仅与物品种类(N)**有关,与V无关的。所以,V很大时(例如上百万),应该是考察搜索。另一方面,N较大时(例如上百),就可能考察动态规划
线性动态规划
这里的线性指的是状态的排布是呈线性的
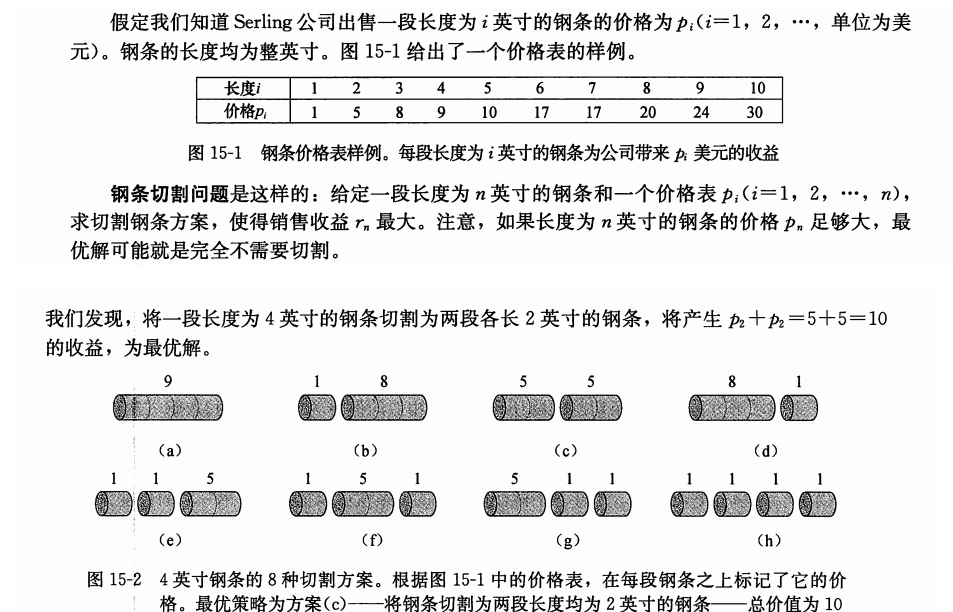

区间模型
区间模型的状态表示一般为d[i][j],表示区间[i, j]上的最优解,然后通过状态转移计算出[i+1, j]或者[i, j+1]上的最优解,逐步扩大区间的范围,最终求得[1, len]的最优解。
给定一个长度为n(n <= 1000)的字符串A,求插入最少多少个字符使得它变成一个回文串
我们用 dp[i][j] 表示对于字符串 s 的子串从[i] 到[j](包含两端),最少添加的字符数量,使得 s[i:j] 变为回文串
从外向内考虑:
- 如果 s[i] == s[j],那么最外层已经形成了回文,我们只需要继续考虑 s[i+1:j-1];
- 如果 s[i] != s[j],那么我们要么在 s[i:j] 的末尾添加字符 s[i],要么在 s[i:j] 的开头添加字符 s[j],取两者最小值
注意该动态规划为区间动态规划,需要注意 dp[i] [j] 的计算顺序。一种可行的方法是,我们递增地枚举子串 s[i:j] 的长度 span = j - i + 1,再枚举起始位置 i,通过 j = i + span - 1 得到 j 的值并计算 dp[i] [j]。这样的计算顺序可以保证在计算 dp[i] [j] 时,状态转移方程中的状态 dp[i + 1] [j],dp[i] [j - 1] 和 dp[i + 1] [j - 1] 均已计算过。
序列化
- 给定一个序列
- 动态规划方程f[i]中的下标i表示前i个元素a[0]、a[1]、…a[i-1]的某种性质
- 坐标型的f[i]表示以ai为结尾的某种性质
- 初始化中,f[0]表示空序列的性质
- 坐标型动态规划的初始条件f[0]就是指以a0为结尾的子序列的性质
LintCode 516 Paint House I
有一排N栋房子,每栋房子要漆成3种颜色中的一种:红、蓝、绿,任何两栋相邻的房子不能漆成同样的颜色,第i栋房子染成红色、蓝色、绿色的花费分别是cost[i] [0],cost[i] [1],cost[i] [2],问最少需要花多少钱油漆这些房子
前N-1栋房子的最小花费的最优策略中,不知道房子N-2是什么颜色,所以有可能和房子N-1撞色,我们只能记录下颜色
因此我们设油漆前i栋房子并且房子i-1是红色、蓝色、绿色的最小花费分别是f[i] [0],f[i] [1],f[i] [2]
通过转移公式:
dp[i][0] = min{
dp[i-1][1] + cost[i][0],dp[i-1][2] + cost[i][0]};
dp[i][1] = min{
dp[i-1][0] + cost[i][1],dp[i-1][2] + cost[i][1]};
dp[i][2] = min{
dp[i-1][0] + cost[i][2],dp[i-1][1] + cost[i][2]};
Paint House II
有一排N栋房子,每栋房子要漆成K种颜色中的一种,任何两栋相邻的房子不能漆成同样的颜色,房子i染成第j种颜色的花费是cost[i][j],问最少需要花多少钱油漆这些房子
这样的话时间复杂度为O(N*K²),有怎么样的优化手段呢
动态规划常见优化手段
同Ⅰ 得出f[i][j]=[min(k!=j){f[i-1][k]}]+cost[i-1][j],其实我们只用计算最小值和次小值,这样的话就不用产生很多重复
这样的话,假设最小值是f[i-1][a],次小值是f[i-1][b],那么f[i][j]=f[i-1][a]+cost[i-1][j],f[i][a]=f[i-1][b]+cost[i-1][a],时间复杂度降为O(N*K)
空间压缩的核心思路就是,将二维数组「投影」到一维数组。也就是d[i] [j]的元素是否跟前一行或者后一行相关,如果相关可以利用temp变量存储起来,只需要用到一维数组。
博弈模型
Nim问题
**定义:**有若干堆石子,每堆石子的数量都是有限的,合法的移动是“选择一堆石子并拿走若干颗(不能不拿)”,如果轮到某个人时所有的石子堆都已经被拿空了,则判负
结论:把每一堆石子的数量进行异或操作,得到结果 res。
若 res != 0,则先手必胜;
若 res == 0,则先手必败;
证明过程:
考虑必胜的局面,就是当先手面对只有一堆石子的情况,这个时候直接全部取走就可以获胜,而这种情况 res 一定满足 res != 0。并且在异或操作中只需要一步就可以把 res != 0 的情况转化成 res == 0 的情况。
因此如果先手面对的局面 res != 0 的话,他就可以一步取走某个数量的石子,将 res == 0 的局面对给对方。
而在 res == 0 的局面下,不管如何取石子,都会破坏这个局面成为 res != 0 的情况。
先手方下回合继续执行上面的步骤即可,这样最终就可以获得游戏胜利。
很多博弈类型都可以转化为Nim问题
特征:
- 在必败态下的任何操作都会转移到必胜态
- 终止状态是必败态
- 能够转移到必败态的是必胜态
Coins in a Line
有一排N个石子,Alice,Bob两人轮流取石子,每次一个人可以从最右边取走一个或两个石子,取走最后石子的人胜,问先手Alice是否必胜
有了Nim问题的特征,我们能轻易写出转移方程
if(f[i-1] == false || f[i-2] == false)
//拿一个或者两个能获胜
f[i] = true;
if(f[i-1] == true || f[i-2] == true)
//必败
f[i] = false;
KMP算法
用 pat 表示模式串,长度为 M,txt 表示文本串,长度为 N。KMP 算法是在 txt 中查找子串 pat,如果存在,返回这个子串的起始索引,否则返回 -1
相对于暴力算法而言,动态规划并不会回退指向txt的指针——因此时间复杂度为O(N)。而是借助dp数组中的信息将pat移到正确的位置继续匹配——因此空间复杂度为O(M)

KMP 算法的难点在于,如何计算 dp 数组中的信息?如何根据这些信息正确地移动 pat 的指针?这个就需要确定有限状态自动机来辅助了
状态机概述
其实j代表的并不是索引,而要理解为状态,我们根据下一字符来决定转移到哪个状态
假设我们匹配的字符串为"ABABC",开始匹配时pat处于初始0状态,5状态表示终止状态,如果遇到除ABC之外的字符直接转移到0状态
状态转移图如下:
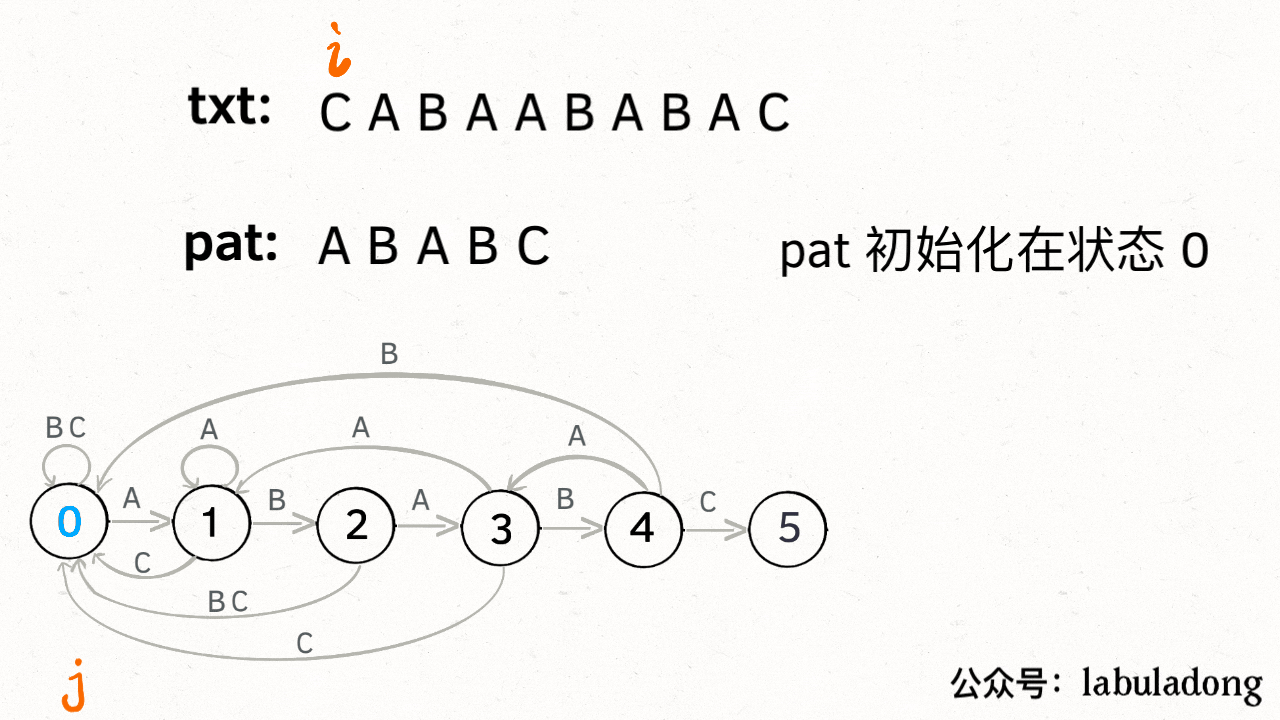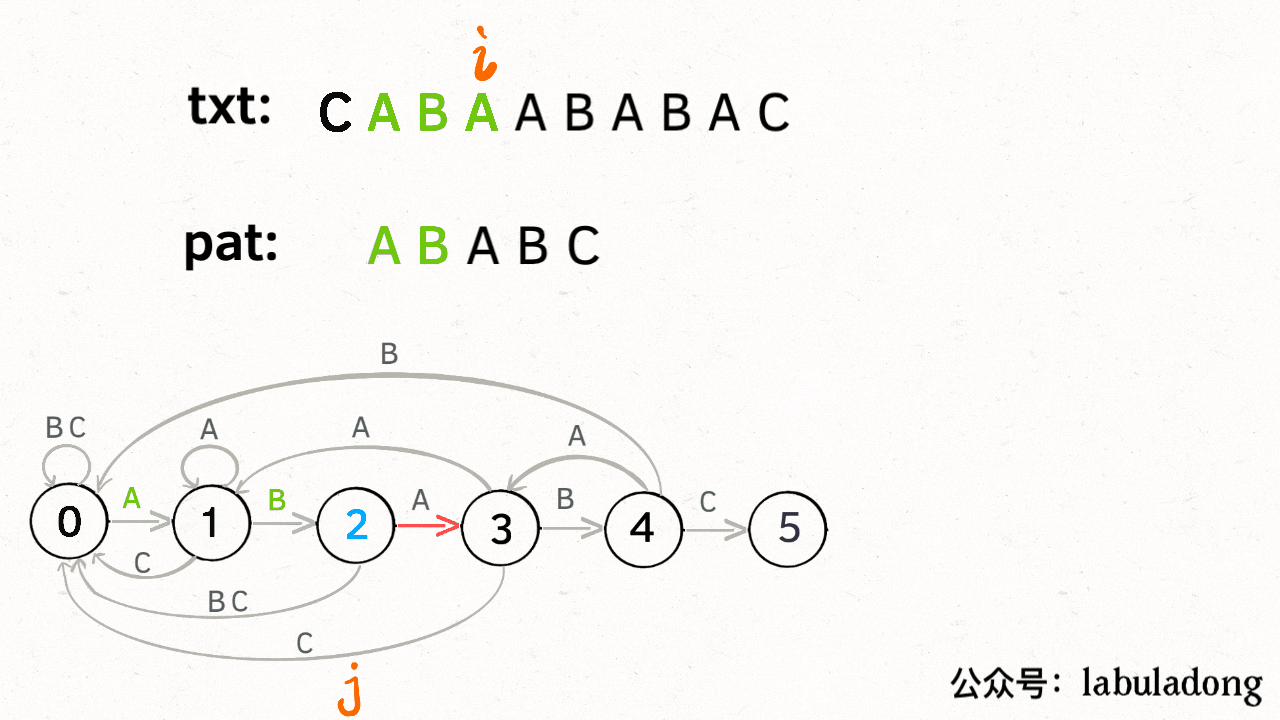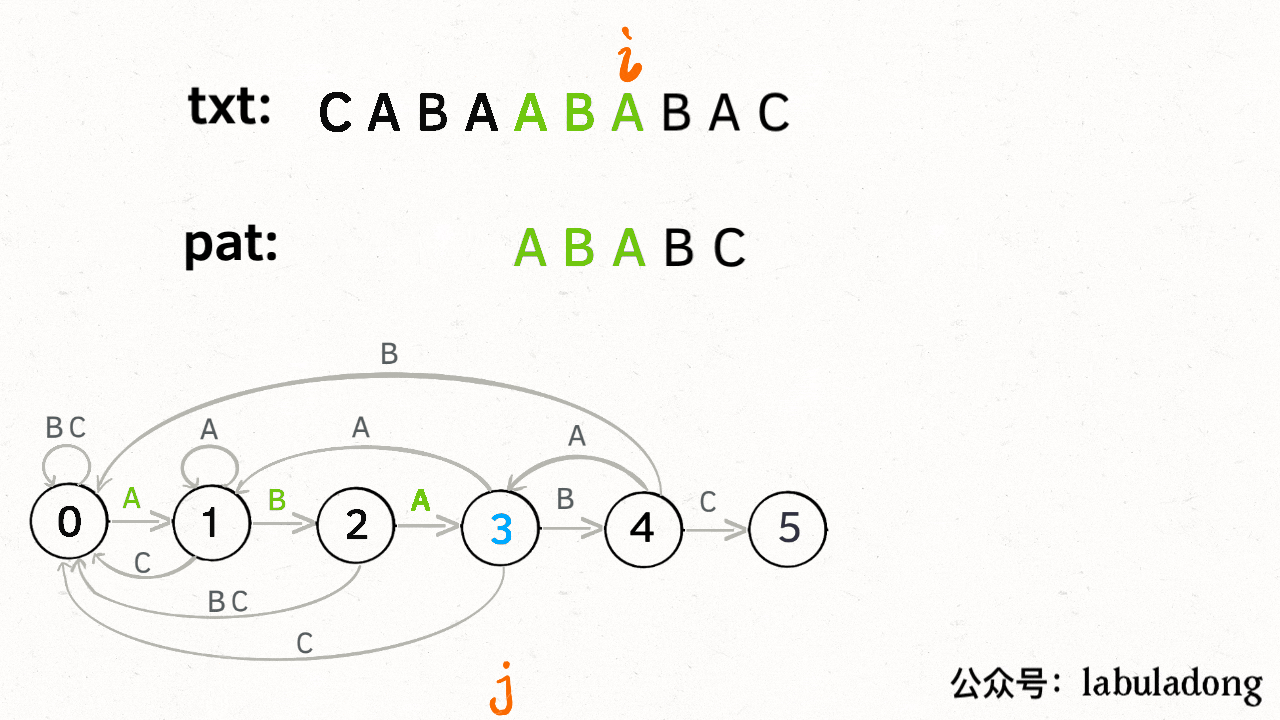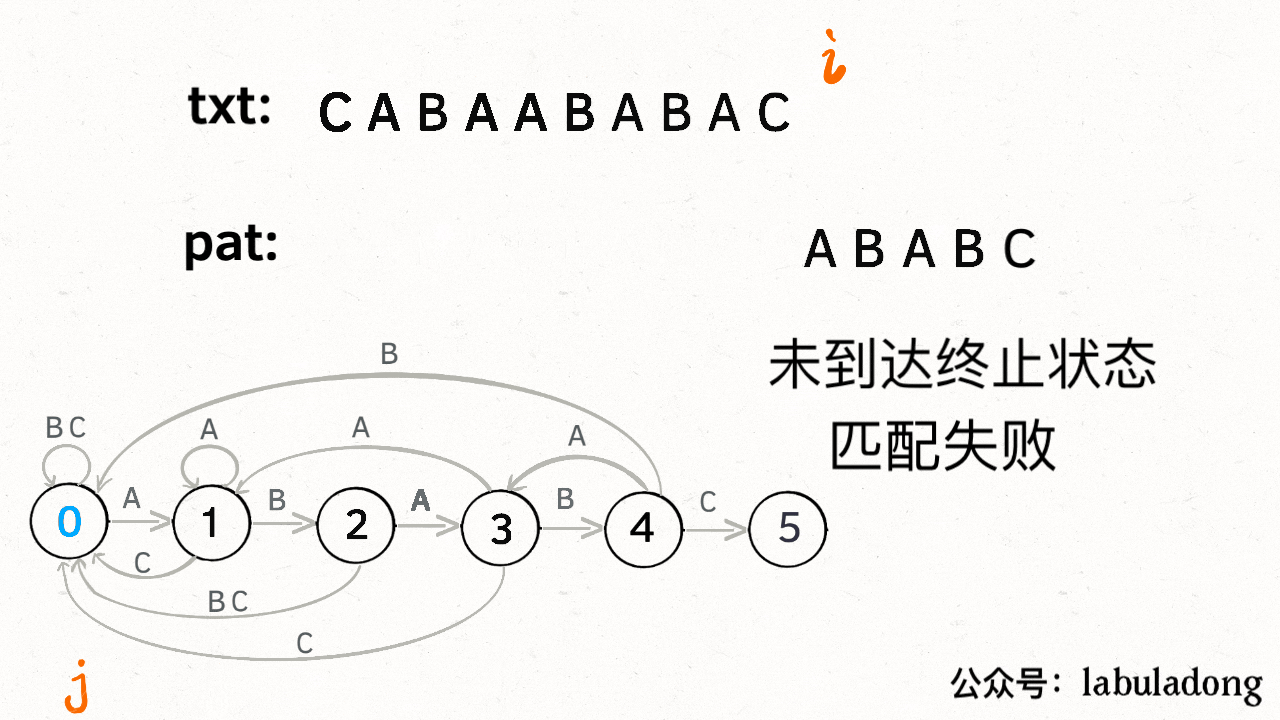
要确定状态转移的行为,得明确两个变量,一个是当前的匹配状态,另一个是遇到的字符;确定了这两个变量后,就可以知道这个情况下应该转移到哪个状态。
我们定义一个二维数组来表示状态转移图:
dp[j][c] = next
0 <= j < M,//代表当前的状态
0 <= c < 256,//代表遇到的字符(ASCII 码)
0 <= next <= M,//代表下一个状态
dp[4]['A'] = 3
//表示:当前是状态 4,如果遇到字符 A,
//pat 应该转移到状态 3
dp[1]['B'] = 2
//表示:当前是状态 1,如果遇到字符 B,
//pat 应该转移到状态 2
//查找函数
public int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
// 如果达到终止态,返回匹配开头的索引
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
构建状态转移图
我们要根据pat字符串构建dp数组,这样在遇到需要匹配多个字符串时还能减少重复操作
这个 next 状态应该怎么求呢?
- 显然,如果遇到的字符
c和pat[j]匹配的话,状态就应该向前推进一个,也就是说next = j + 1,我们不妨称这种情况为状态推进: - 如果字符
c和pat[j]不匹配的话,状态就要回退(或者原地不动),我们不妨称这种情况为状态重启: - 我们需要在和当前状态具有相同的前缀的位置重启,用变量X来表示
- 当前状态
j = 4,其影子状态为X = 2,它们都有相同的前缀 “AB”。因为状态X和状态j存在相同的前缀,,可以通过X的状态转移图来获得最近的重启位置。也就是dp[j]['A'] = dp[X]['A']:——X怎么知道遇到字符 “B” 要回退到状态 0 呢?因为X跟在j的身后,状态X如何转移,在之前就已经算出来了。动态规划算法就是利用过去的结果解决现在的问题
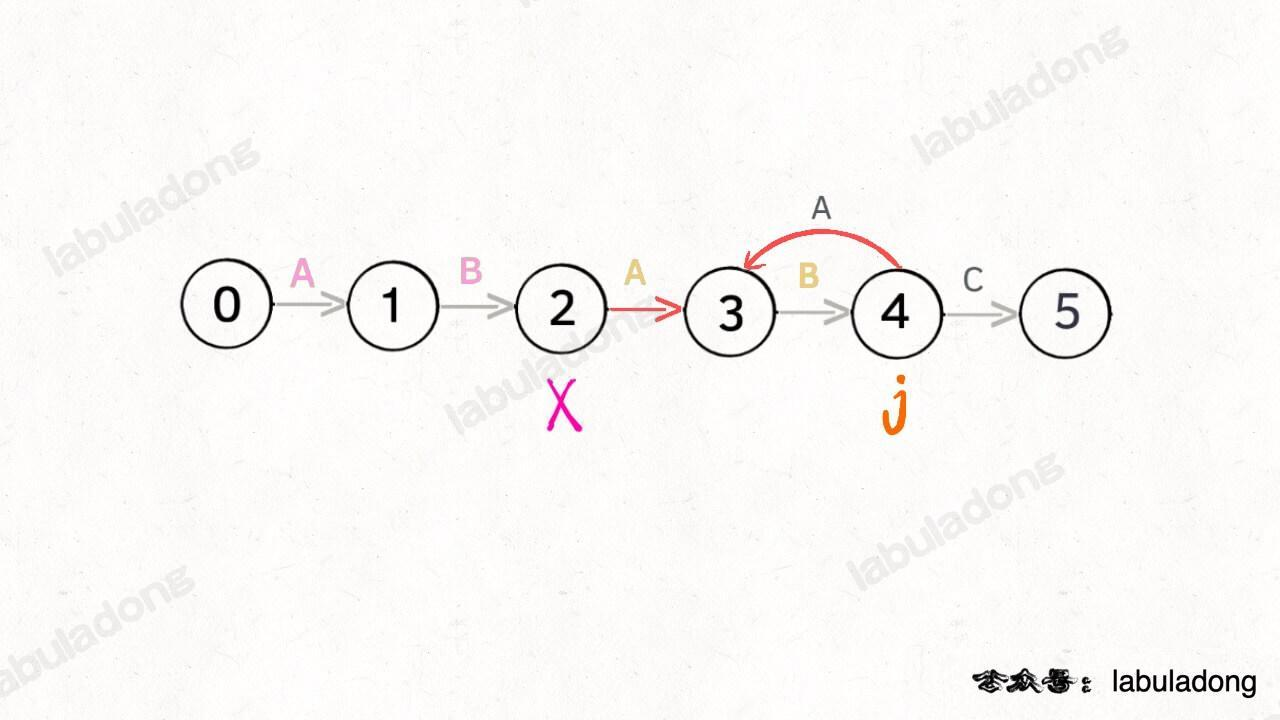
现在还有一个问题, X 是如何得到?
影子状态 X 是先初始化为 0,然后随着 j 的前进而不断更新的,更新 X 其实和 search 函数中更新状态 j 的过程相似
注意代码中 for 循环的变量初始值,可以这样理解:后者是在 txt 中匹配 pat,前者是在 pat 中匹配 pat[1..end],状态 X 总是落后状态 j 一个状态,与 j 具有最长的相同前缀
//更新状态 X
int X = 0;
for (int j = 1; j < M; j++) {
...
// 更新影子状态
// 当前是状态 X,遇到字符 pat[j],
// pat 应该转移到哪个状态?
X = dp[X][pat.charAt(j)];
}
//更新状态 j
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
...
}
完整构造图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RdxygKm7-1660201693147)(动态规划刷题个人总结/dfa.gif)]
完整代码:
public class KMP {
private int[][] dp;
private String pat;
//构建状态转移图
public KMP(String pat) {
this.pat = pat;
int M = pat.length();
// dp[状态][字符] = 下个状态
dp = new int[M][256];
// base case
dp[0][pat.charAt(0)] = 1;
// 影子状态 X 初始为 0
int X = 0;
// 构建状态转移图(稍改的更紧凑了)
for (int j = 1; j < M; j++) {
for (int c = 0; c < 256; c++)
dp[j][c] = dp[X][c];
dp[j][pat.charAt(j)] = j + 1;//状态前进
// 更新影子状态
X = dp[X][pat.charAt(j)];
}
}
//搜索函数
public int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 计算 pat 的下一个状态
j = dp[j][txt.charAt(i)];
// 到达终止态,返回结果
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
}