感谢前辈大佬,引用自:
[1] http://users.rowan.edu/~polikar/WTpart3.html,
[2] https://www.cnblogs.com/sggggr/p/11872450.html
加上了一些自己的整理和总结,完全的DSP小白,作为交叉学科的起征点敬上。侵删!
一、背景
在传统的傅里叶分析中,信号完全是在频域展开的,不包含任何时频的信息。因为丢弃的时域信息对某些应用同样重要,所以出现很多能表征时域和频域信息的信号分析方法,如短时傅里叶变换、Gabor 变换、时频分析、小波变换等。
其中,短时傅里叶变换是在傅里叶分析基础上引入时域信息的最初尝试,在假定一定长度时间窗内的信号是平稳的前提下,短时傅里叶变换可以通过将每个时间窗内的信号展开到频域的方法来获得局部的频域信息。但是,短时傅里叶变换的时域区分度只能依赖于大小不变的时间窗,对某些瞬态信号来说还是粒度太大。所以,对很多应用来说不够精确,短时傅里叶变换仍存在很大的缺陷。
STFT给信号加窗,分段做FFT。而小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间。小波分析克服了短时傅里叶变换在单分辨率上的缺陷,具有多分辨率分析的特点,在时域和频域都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态动态调整。在一般情况下,在低频部分(信号较平稳)可以采用较低的时间分辨率来提高频率的分辨率,在高频情况下(频率变化不大)可以用较低的频率分辨率来换取精确的时间定位。因为这些特性,小波分析可以探测正常信号中的瞬态,并展示其频率成分,被称为数学显傲镜,广泛应用于各个时频分析领域。
二、连续小波变换 (CWT, Continuous Wavelet Transformation)
连续小波变换是作为短时傅里叶变换的替代方法而开发的,以克服分辨率问题。小波分析的完成方式与STFT分析类似,从某种意义上说,信号与一个小波函数相乘,类似于STFT中的窗口函数,并且针对时域信号的不同段分别计算变换。但是,STFT和CWT之间有两个主要区别:
(1) 不采用窗口信号的傅里叶变换,因此将看到对应于正弦波的单个峰值,即不计算负频率。
(2) 随着每个光谱分量的变换计算,窗口的宽度会发生变化,这可能是小波变换的最显着特征。
连续小波变换定义如下:
如上式所示,变换后的信号是两个变量tau和s的函数,分别是平移translation和尺度scale参数。psi是变换函数,它被称为母小波。
母小波因小波分析的两个重要性质而得名:
(1) 小是指此(窗口)函数长度有限(紧凑支持)的条件。
(2) 波是指此功能振荡的条件。母意味着变换过程中使用的具有不同支持区域的函数来自一个主函数或母小波。换句话说,母小波是生成其他窗口函数的原型。
2.1 参数:尺度scale
小波分析中的尺度类似于地图中使用的比例。与地图的情况一样,高尺度对应于(信号的)非详细全局视图,而低尺度对应于详细视图。同样,就频率而言,低频(高尺度)对应于信号的全局信息(通常跨越整个信号),而高频(低尺度)对应于信号中隐藏模式的详细信息(通常持续相对较短的时间)。下图给出了各种尺度对应的余弦信号作为示例。
缩放作为一种数学运算,可以放大或压缩信号。较大的尺度对应于扩张(或拉伸)信号,小尺度对应于压缩信号。图中给出的所有信号都来自相同的余弦信号,即它们是同一函数的膨胀或压缩版本。在上图中,s = 0.05是最小尺度,s = 1是最大尺度。
在数学函数方面,如果 f(t) 是一个给定的函数,如果s > 1,f(st) 对应于 f(st) 的收缩(压缩)版本,如果s < 1,则对应于 f(t) 的扩展(膨胀)版本。然而,在小波变换的定义中,s在分母中,因此,与上面相反,尺度s > 1 代表膨胀信号,而标度s < 1 压缩信号。
2.2 CWT的计算
使用的所有窗口都是母小波的扩张(或压缩)和移位版本。Morlet 小波和墨西哥帽子函数是两个候选函数。一旦选择了母小波,连续小波变换将计算从s =1开始,s小于和大于’‘1’'的所有值。但是,根据信号的不同,通常不需要取值完全。现实中,信号是有带宽限制的,因此,计算有限s间隔的变换通常就足够了。该过程将从尺度s=1开始,将s递增,即分析将从高频开始,然后向低频进行。s的第一个值将对应于最压缩的小波。随着s值的增加,小波会膨胀。
小波放置在信号的开头,对应于时间 tau = 0 的点。s为“1”的小波函数乘以信号,然后在所有时间进行积分。然后将积分的结果乘以常量
![]()
此乘法用于能量归一化,以便转换后的信号在每个尺度上都具有相同的能量。
最终结果是变换的值,即在时间 tau = 0 和尺度 s = 1 处连续小波变换的值。换句话说,它是对应于点 tau = 0,s = 1在时频平面(即尺度-平移坐标系)的值。重复该过程,直到小波到达信号的末端,对应出现在时频平面上s=1的一行点。然后,s增加一个小值。请注意,这是一个连续的变换,因此,tau和s都必须连续递增。但是,如果此变换需要由计算机计算,则两个参数都会以足够小的步长递增。这对应于对时间尺度平面进行采样。对 s 的每个值重复上述过程。给定值 s 的每次计算都会填充时频平面的相应单行。当所有所需值 s 的过程完成时,已经计算出信号的CWT。
下图逐步说明了整个过程。
信号:
s为1,对应于最低尺度或最高频率。注意它有多紧凑(蓝色窗口)。它应该与信号中存在的最高频率分量一样窄。在每个位置,它都会乘以信号。显然,乘积仅在信号落在小波支撑区域的地方不为零,而在其他地方为零。通过时间上移动小波,信号在时间上被定位,通过改变s的值,信号在尺度(频率)上被定位。如果信号具有对应于 s 的当前值(在本例中为 1)的频谱分量,则小波与该频谱分量所在位置的信号的乘积给出了一个相对较大的值。如果信号中不存在与s的当前值对应的频谱分量,则乘积值将相对较小或为零。图3.3中tau =100 ms的信号周围具有与s= 1窗口宽度相当的光谱分量。
尺度s = 5和s = 20的相同过程。请注意窗口宽度如何随着比例的增加(频率降低)而变化。随着窗口宽度的增加,变换开始拾取较低频率的分量。
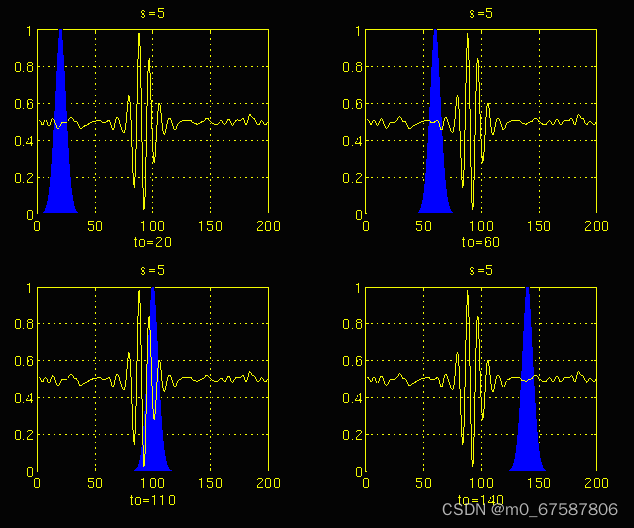

因此,对于每个尺度和每个时间(间隔),将计算时间尺度平面的一个点。一个尺度的计算构造时间尺度平面的行,不同尺度的计算构造时间尺度平面的列。
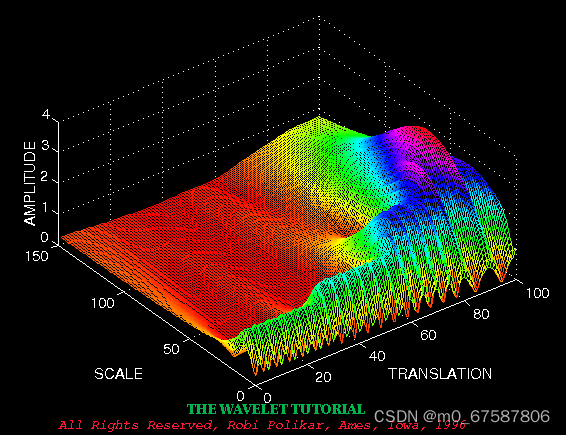
现在,让我们看一个例子,看看小波变换的真实情况。如图所示,信号由 30 Hz、20 Hz、10 Hz 和 5 Hz 的四个频率分量组成。

下图是该信号的连续小波变换(CWT)。请注意,轴是平移和尺度,而不是时间和频率。但是,平移与时间严格相关,因为它指示母小波的位置。母小波的平移可以被认为是自t = 0 以来经过的时间,而刻度参数s实际上是频率的反比。
较小的尺度对应于较高的频率,即频率随着尺度的增加而降低,因此,图中刻度约为零的部分实际上对应于分析中的最高频率,而具有高尺度的部分对应于最低频率。请记住,信号首先具有 30 Hz(最高频率)分量,这出现在 0 到 30 的转换的最低尺度上。然后是 20 Hz 分量、第二高频率等。5 Hz 分量出现在平移轴的末端(如预期),并按预期再次出现在较高尺度(较低频率)上。
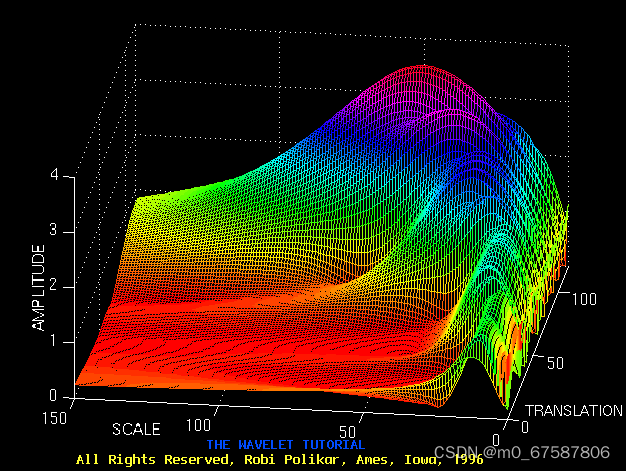
与在任何时候和频率上都具有恒定分辨率的STFT不同,WT在高频下具有良好的时间和较差的频率分辨率,在低频下具有良好的频率和较差的时间分辨率。
下图中,较低的尺度(较高的频率)具有更好的尺度分辨率(尺度较窄,这意味着尺度的确切值不太模糊),对应于较差的频率分辨率。同样,较高的频率具有尺度频率分辨率(在尺度上有更广泛的范围,这意味着尺度更准确),对应于较低频率更好的频率分辨率。
粗略地说,平移轴上的 100 个点对应于 1000 ms,刻度轴上的 150 个点对应于 40 Hz 的频段(平移轴和尺度轴上的数字分别不对应于秒和 Hz,它们只是计算中的样本数)。
三、离散小波变换 (DWT, Discrete Wavelet Transformation)
CWT可以看做是不同尺度的小波和信号的相关运算,其结果表征了信号与不同尺度小波的相似程度。改变分析窗的尺度,在时间上移动窗函数,并将其与信号相乘来计算连续小波变换。在离散的情况下,用不同截止频率的滤波器在不同的尺度上对信号进行分析。信号通过一组高通滤波器来分析其高频分量,通过一组低通滤波器分析其低通分量。信号的分辨率这个信号详细信息的表征方法,会随着滤波方式而变化。尺度通过上采样(upsampling)和下采样(downsampling)而变化。下采样一个信号指的是降低信号采样率,或者说去除一些信号中的采样点。例如,2倍的下采样指的是信号每隔一个采样点保留一个值。n倍的下采样则是将采样点降为1/n。
上采样一个信号指的则是通过对原始信号增加采样点数来提高信号采样率。例如,2倍的上采样指的是在每两个相邻的采样点之间增加一个新的采样点,其值通常为0。n倍的上采样则是在通过增加n倍的采样点数来将采样率提高n倍。信号序列将由 x[n] 表示,其中 n 是整数。该过程首先将该信号(序列)通过具有脉冲响应h[n]的半频段数字低通滤波器。滤波信号对应于信号与滤波器脉冲响应卷积的数学运算。离散时间中的卷积运算定义如下:

半带低通滤波器可消除信号中高于最高频率一半的所有频率。例如,如果信号具有最大1000 Hz的分量,则半带低通滤波会去除500 Hz以上的所有频率。
DWT通过将信号分解为粗略的近似值和详细信息来分析不同频段的信号,具有不同的分辨率。DWT 采用两组函数,称为缩放函数和小波函数,它们分别与低通和高通滤波器相关联。信号分解为不同的频段,只需对时域信号进行连续的高通和低通滤波即可获得。原始信号x[n]首先通过半带高通滤波器g[n]和低通滤波器h[n]。
这种分解使时间分辨率减半,因为现在只有一半的样本数量来表征整个信号。然而,这种操作使频率分辨率加倍,因为信号的频带现在仅跨越先前频带的一半,从而有效地将频率的不确定性降低了一半。上述过程也称为子带编码,可以重复以进行进一步分解。在每个级别,滤波和子采样将导致一半的样本数量(因此一半的时间分辨率)和一半的跨频带(因此频率分辨率翻倍)。图4.1说明了此过程,其中x[n]是要分解的原始信号,h[n]和g[n]分别是低通和高通滤波器。每个阶段的信号带宽在图上标记为“f”。
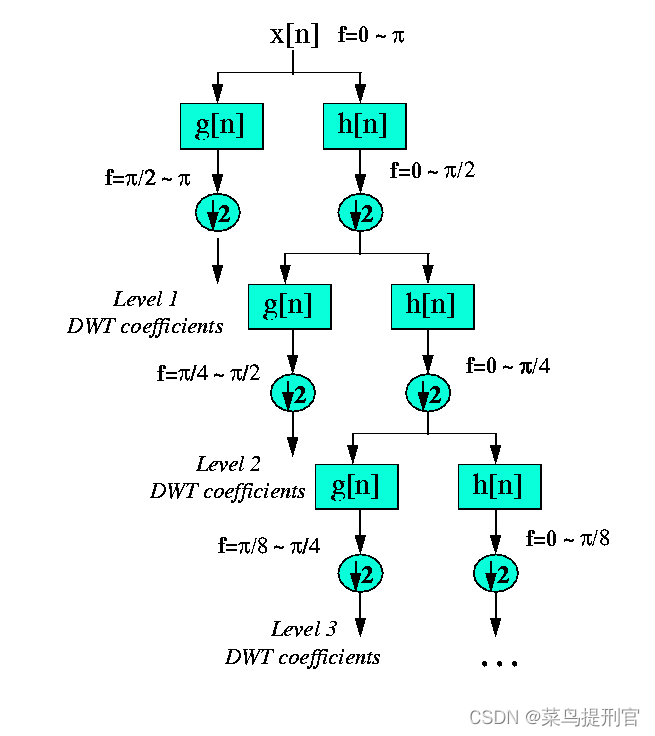
例如,假设原始信号 x[n] 有 512 个采样点,跨越 0 到 p rad/s 的频带。在第一个分解级别,信号通过高通和低通滤波器,然后子采样2。高通滤波器的输出有256个点(因此是时间分辨率的一半),但它只跨越频率p/2到p rad/s(因此频率分辨率是两倍)。这256个样本构成了DWT系数的第一级。低通滤波器的输出也有256个样本,但它跨越了频带的另一半,频率从0到p/2 rad/s。然后,该信号通过相同的低通和高通滤波器进行进一步分解。第二个低通滤波器后跟子采样的输出有 128 个样本,频带为 0 到p/4 rad/s,第二个高通滤波器后跟子采样的输出有 128 个样本,跨越p/4 到 p/2的频带。第二个高通滤波信号构成DWT系数的第二级。该信号具有一半的时间分辨率,但频率分辨率是第一级信号的两倍。换句话说,与原始信号相比,时间分辨率降低了4倍,频率分辨率提高了4倍。然后再次对低通滤波器输出进行滤波,以便进一步分解。这个过程一直持续到剩下两个样品。对于此特定示例,将有 8 个级别的分解,每个级别的样本数量是前一个级别的一半。然后通过连接从最后一个分解级别开始的所有系数(在本例中为剩余两个样本)来获得原始信号的 DWT。然后,DWT 将具有与原始信号相同数量的系数。
原始信号中最突出的频率将在包含这些特定频率的 DWT 信号区域中显示为高振幅。这种变换与傅里叶变换的区别在于,这些频率的时间定位不会丢失。但是,时间本地化的分辨率取决于它们显示的级别。如果信号的主要信息位于高频中,就像最常见的那样,这些频率的时间定位将更加精确,因为它们的特点是样本数量更多。如果主要信息仅在非常低的频率上,则时间定位不会非常精确,因为很少有样本用于表达这些频率下的信号。此过程实际上在高频下提供了良好的时间分辨率,在低频下提供了良好的频率分辨率。遇到的大多数实际信号都是这种类型的。