机器学习——模型评估和选择

经验误差与过拟合

误差

• 错误率：分类错误的样本占样本总数的比例：
  $E=\frac{a}{m}$ m 个样本中有 a 个样本分类错误
• 误差：学习器的实际预测输出值与样本真实输出值之间的差异。
• 训练误差：学习器在训练集上的误差，也叫经验误差。
• 泛化误差：在新样本上的误差。
    机器学习上，我们希望得到泛化误差小的学习器。比如我有一个区分性别的分类器，它不仅可以区分动物的性别，把它用到单性花上也能很好的区分出雌雄株。然而我们并不知道新样本长啥样，所以我们努力做到训练误差最小化。很多情况下，我们可以做到经验误差很小，对多有的训练样本分类全部正确，这是不是我们想要的学习器呢？不幸的是：这种学习器的泛化能力一般很小，对待新样本多数情况下都不好。

过拟合与欠拟合

• 过拟合： 学习样本学得太好了，很可能已经把训练样本自身的一些特点当做了所有样本都具有的一般性质，这样会导致泛化能力的下降，就是偏科的同学
• 欠拟合： 对训练样本的一般性质都没有学好，就是差生，一样的不行。
  

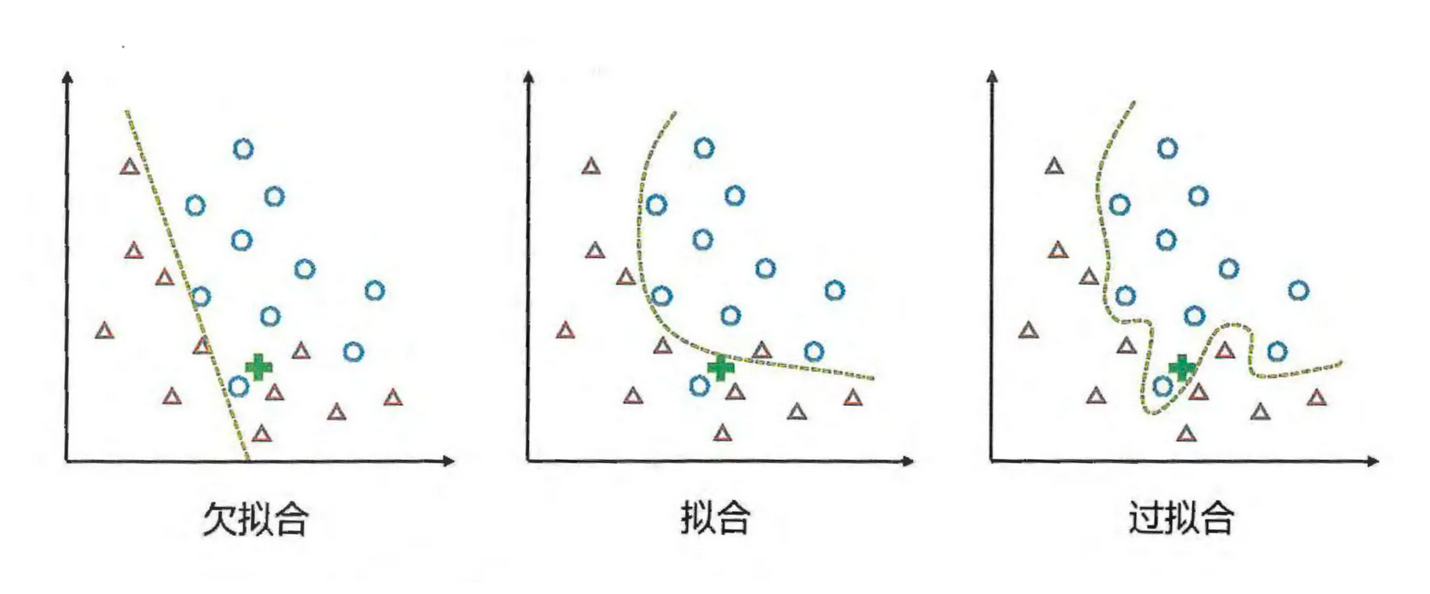
  我们希望在新的样本身上学习器仍然能够表现得更好，所以我们要尽可能的从训练样本中学出适用于所有潜在样本的“普遍规律”，这样就可以对新的样本做出正确的判断。
  很多因素都会导致过拟合，其中最常见的情况就是机器学习过于强大，以至于把训练样本所包含的不太普遍的特性都学到了。欠拟合就是学习能力不足的情况，这种情况我们容易解决，而过拟合则很麻烦。 在后面的学习中我们会看到过拟合是机器学习的关键障碍，各类算法都必然携带针对过拟合的措施；我们需要认识到过拟合无法彻底避免，只能缓解。

评估方法

  我们希望得到训练好的模型，就是要让学习器举一反三，那么我们的训练集和测试集就要分开才能到达很好的评估效果。如同我们学习一样，练习题做得滚瓜烂熟，期末考试考原题，满分是必然的吧，不满分扣个5分也有95分。遇到牛人，直接背试卷ABCD,也满分。这样当然不好，没有把练习题和考试题分开啊。我们来看看机器学习的“考试方法”

1.留出法(hold-out)

  直接将数据集D分为两个互斥集合，一个训练集合S,和一个测试集合T, D = S U T ,S ∩ T = ∅；学习器在S集合行训练出模型，然后再用集合T测试误差，作为泛化误差的估计。
  煮个栗子：100个样本，分给训练集有 60 个样本，测试集30个样本。我们训练60个样本中，分类正确的有56个,错误分类4个。
$$\begin{array}{rl}错误率& =\frac{4}{60}=0.067\\ 精度& =0.933\end{array}$$
  注意： 训练集和测试集的划分要尽量保持和原数据一致性.你不能这样，训练集中的数据基本都是单一的数据，特征也基本一致，而测试集的数据则稀奇古怪，三类四类的都有。这种划分就不合理，最后就会导致，训练误差很小，测试出来的泛化误差就很大。
  单次使用留出法得到的估计结果往往不稳定不可靠。我们一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。 比如进行 100 次随机划分，每次产生一个 训练集 / 测试集 用于实验评估，就有100 个结果，我们返回这 100 个结果的平均值。
  但是哪个比列才更好呢？如果训练集 S 包含绝大多数样本，则训练出的模型可能更接近于总集合D训练出的模型，但是测试集T就少了，评估结果可能不够稳定准确；反过来测试集T多包含样本，训练集S训练度可能不够，与总集合D差别更大了，降低了评估结果的保真性。这个问题没有完美的解决方案，我们一般将 $\frac{2}{3}$~$\frac{4}{5}$ 的数据用于训练，其他的部分用来测试

2.交叉验证法

  所谓的“交叉验证法”就是现将数据集 D 划分为 k 个大小相似的互斥子集，即
$D$ = $D_1$U$D_2$U…U$D_k$,  $D_i$∩$D_j$=∅（i≠j）
每个子集$D_i$尽可能保持数据分布的一致性，即从D中通过层次采样得到。然后每次使用 k - 1个子集的并集作为训练集，余下的哪个子集作为测试集，这样就可以获得 k 组 训练集 / 测试集，就可以进行 k 次训练和测试，最终返回 K 个训练结果的均值。
  交叉验证法评估结果的稳定性和保真性在很大程度上取决于 k 值，为了强调这一点，我们又称“k折交叉验证” k 的最常用取值是10，也有用5,20的。来看一张图把，助于理解。
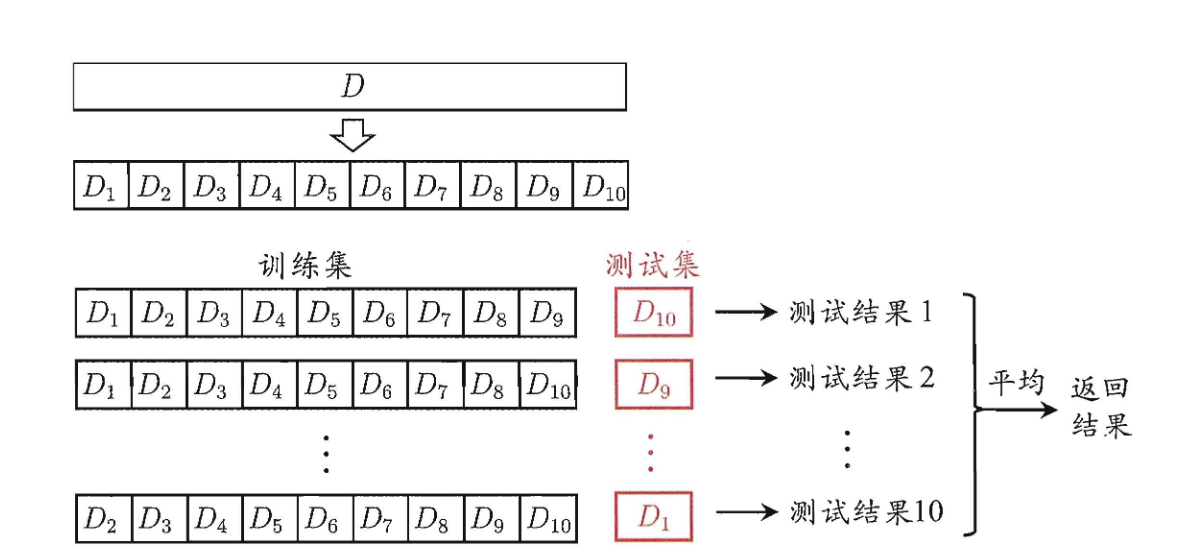  如果我们数据集D包含m个样本，又 k = m，就得到了交叉验证法的一个特例：留一法（Leave-One-Out，简称LOO）

• 优点：由于m个样本只有唯一的方式划分为m个子集——每个子集只有一个样本，划分就没有影响了。留一法使用的训练集与原始数据相比至少了一个样本，在绝大多数情况下，实际评估的模型和用D评估出来的模型很相似，结果往往比较准确。
• 缺点：我们处在大数据阶段呢，数据是爆炸式的增长。在数据集比较大时，训练m个模型的计算机开销可能难以承受的。1000万的数据就要训练1000万次，如果加上神经网络里算法面的参数，直接gg。

3.自助法

  直接以自助采样为基础。给定 m 个样本的数据集 D,我们对其进行采样产生数据集 D’：每次随机从D中选取一个样本，将其拷贝放入D’，然后再将样本放回数据集D中，使得该样本在下次采样中仍可能被采到；重复 m 次，就收集到了 m 个数据集 D’，这就是自助采样的结果。D中有一部分数据会多次出现，而另一部分数据则不会出现。我们可以做一个简单的估计。样本在 m 次采样中始终不会采到的概率是${(1-\frac{1}{m})}^m$,取极限：
$$\underset{m->+\infty }{\lim }{(1-\frac{1}{m})}^m=\frac{1}{e}\approx 0.368$$
  通过自助采样，初始数据集D中有36.8%的样本未出现在采集数据集 D’ 中。我们将D’用来训练，D \ D’用作测试集。

• 优点：实际评估的模型与期望评估的模型都使用了 m 个训练样本，而我们仍然有数据总量的 1/3 没在训练集出现的样本用于测试。这个结果也叫“包外估计”，在训练集较小，难以划分 训练集 / 测试集时很常用，并且能从初始数据集D中产生多个不同的数据集，对集成学习等方法有很大的好处。
• 缺点 ：改变了初始数据集的分布，引入估计偏差，数据集较大时，留出法和交叉验证法更常用。

性能量度

  性能量度也是衡量模型泛化能力的评价标准。 它反应了任务需求，在对比不同模型能力时，使用不同的性能量度往往会导致不同的批判结果。模型的好坏是相对的，什么样的模型什么时候是好的，不仅取决于算法和数据，还决定于任务需求。
  在预测任务中，给定样例集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D = \left \{ {(x_1,y_1),(x_2,y_2),...,(x_m,y_m)} \right \} D={ (x1​,y1​),(x2​,y2​),...,(xm​,ym​)}
其中 $y_i$ 表示 $x_i$ 的真实标记。要评估学习器 f 的性能，就要把学习器预测的结果 $f(x)$ 与真实 $y$ 进行比较。

• 回归任务最常用的性能量度是“均方误差” $$E(f:D)=\frac{1}{m}\sum _{i=1}^m(f(x_i)-y_i{)}^2$$
• 对于数据分布 D 和概率密度函数 $p(\cdot )$,均方误差可描述为：$$E(f:D)={\int }_{x\sim D}(f(x)-y{)}^{2}p(x_i)dx$$
    这里是常用的性能量度。

1.错误率与精度

  这是分类任务中最常用的两种性能量度，既适用于二分类，也适用于多分类任务。错误率是分类错误的样本数占样本总数的比例，精度则是分类正确的样本数占总数的比例。
  对于样本集 D 分类错误率定义为：
$$E(f;D)=\frac{1}{m}\sum _{i=1}^m\left|\right|(f(x_i)\ne y_i)$$
  精度定义：
$$\begin{array}{rl}acc（f;D)& =\frac{1}{m}\sum _{i=1}^m\left|\right|(f(x_i)=y_i)\\ & =1-E(f;d)\end{array}$$
  更一般的，对于数据分布 D 和概率密度函数 $p(\cdot )$ ,错误率与精度可分别描述为
$$\begin{array}{rl}E(f;D)& ={\int }_{x\sim D}\left|\right|(f(x)\ne y)p(x)dx,\\ acc(f;D)& ={\int }_{x\sim D}\left|\right|(f(x)=y)p(x)dx\\ & =1-E(f;D)\end{array}$$

2.查准率、全差率与F1

  错误率和精度虽然常用，但并不能满足所有任务 需求，这里我们将要引入查准率和全差率。对于二分类问题，我们可以将样例根据其真实类别与学习器预测类别的组合划分为：真正例、假正例、真反例、假反例 四种情况，令其 TP , FP,TN,FN 分别表示其对应的样例数，那么有：TP + FP + TN + FN = 样例总数。我们可以得到一个分类结果的“混淆矩阵”：
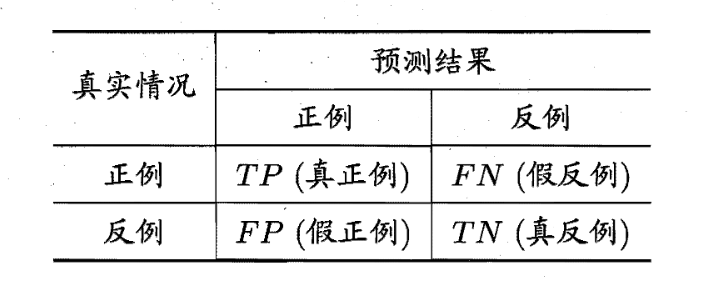  查准率P和全差率R分别定义为：
$$\begin{array}{rl}P& =\frac{TP}{TP+FP}\\ R& =\frac{TP}{TP+FN}\end{array}$$
  查准率和查全率是一对矛盾的度量。一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。 我们可以利用西瓜集这样记：
$$\begin{array}{rl}& \\ 查准率P& =\frac{猜对的好西瓜(全对)}{猜出的好西瓜(预测集输出为好)}\\ & \\ 查全率R& =\frac{猜对的好西瓜(全对)}{所有的好西瓜(属于全集中)}\end{array}$$
  在很多情况下，我们可以根据学习器的预测结果对样例进行排序，排在前面的的是学习器认为“最可能”是正例的样本，排在最后的则是学习器认为“最不可能”是正例样本。按照这个顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率，查准率。再以查全率为横轴、查准率为纵轴做出“P-R”图。

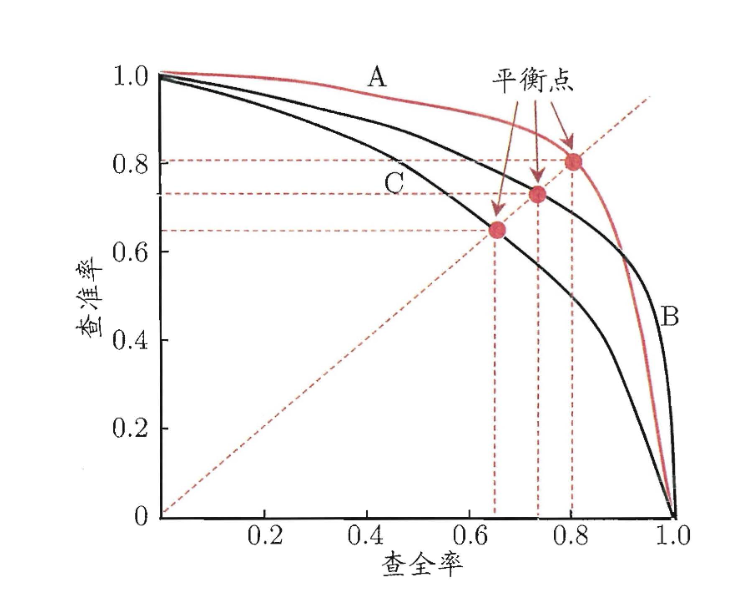
  我们可以直观的看出曲线的分布，那根曲线在上面，哪个学习器的性能就越好。 但是实际情况下我们的曲线基本会相交，而我们却偏要找出一个更好的，在这种情况下，我们设计了一些综合考虑查准率、查全率的性能量度。平衡点（BEP） 就是这样一个量度，它是“查准率=查全率”时的取值,上图的C的 BEP 在0.64左右，基于 BEP 的比较，可以认为 A 优于 B.但是 BEP过于粗暴了，我们可以如下处理。

• 更常用 F1度量：$$F_1=\frac{2P\cdot R}{P+R}=\frac{2\cdot TP}{样例总数+TP-TN}$$
• 在一些应用中，对查准率和查全率的重视程度有所不同。比如我们看抖音，为了尽可能使推荐内容是用户感兴趣的，此时查准率更重要。我们在检索逃犯信息是，查全率就更为重要。对 F1 度量的一般形式——Fβ，他可以让我们表达出对查准率 / 查全率 的不同偏好：$$F_{\beta }=\frac{(1+{\beta }^2)\cdot P\cdot R}{({\beta }^2\cdot P)+R}$$ 其中β>0度量了查全率对查准率的相对重要性。β = 1就退化为标准的F1；β > 1查全率有更大的影响；β < 1查准率有较大的影响。
• 很多时候我们有多个二分类矩阵，我们希望从 n 个二分类混淆矩阵综合考虑查准率和查全率。在混淆矩阵上分别计算出查准率、查全率，记为$(P_1,R_1),(P_2,R_2),...,(P_n,R_n)$再计算平均值，得到“宏查准率”(macro-P)、“宏查全率”(macro-R)、“宏F1”(macro-F1):$$\begin{array}{rl}macro-P& =\frac{1}{n}\sum _{i=1}^n{P}_i,\\ macro-R& =\frac{1}{n}\sum _{i=1}^n{R}_i,\\ macro-F_1& =\frac{2\times macro-P\times macro-R}{macro-P+macro-R}\end{array}$$
• 将各混淆矩阵对应的元素进行平均，得到TP,FP,TN,FN的平均值，分别记为$\overline{TP},\overline{FP},\overline{TN},\overline{FN},$再基于这些平均值计算出“微查准率”(micro-P)、“微查全率”(micro-R)、“微F1”(micro-F1):$$\begin{array}{rl}micro-P& =\frac{\overline{TP}}{\overline{TP}+\overline{FP}},\\ micro-R& =\frac{\overline{TP}}{\overline{TP}+\overline{FN}},\\ micro-F_1& =\frac{2\times micro-P\times micro-R}{micro-P+micro-R}\end{array}$$

3.ROC与AUC

  ROC全称“受试者工作特征”（Recevier Operating Characteristic）,与P-R曲线相似，我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要的值，分别以它们为横、纵坐标图就得到了“ROC”图，纵轴是“真正例率(TPR)，横轴是假正率例(FPR)” :$$\begin{array}{r}TPR=\frac{TP}{TP+FN},\\ FPR=\frac{FP}{FP+TN}\end{array}$$

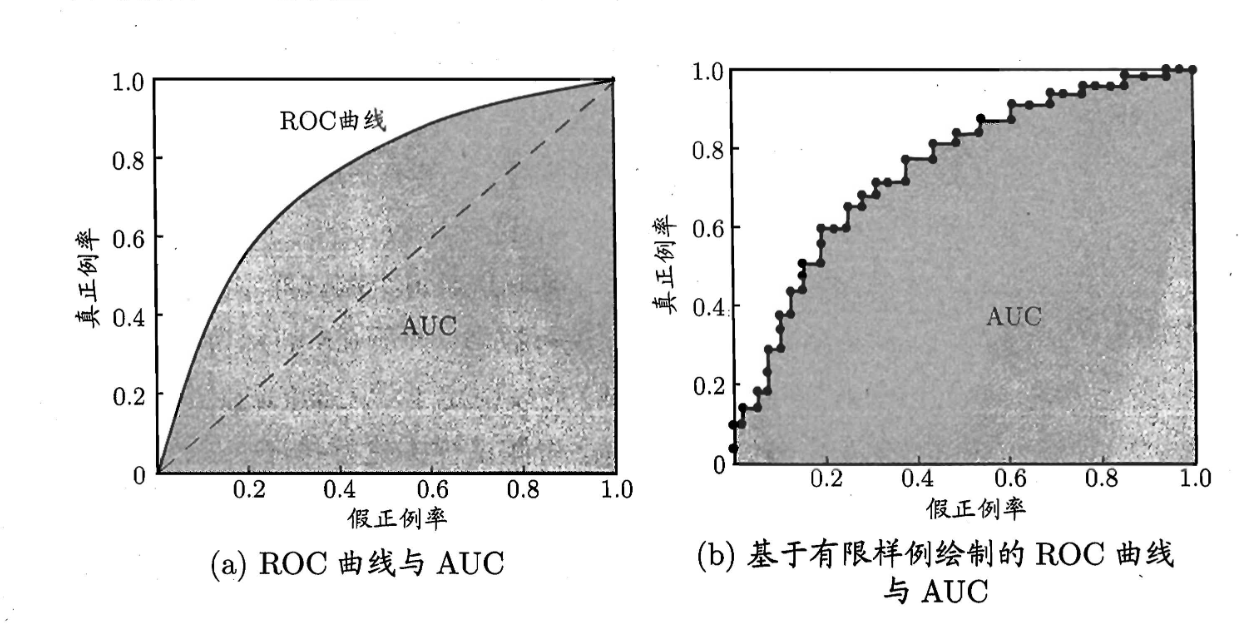  现实任务中通常是利用有限个测试样例来绘制ROC图，此时仅能获得有限个（真正例率，假正率例）坐标对，无法产生光滑的ROC曲线绘图过程：给定$m^{+}$个正例和$m^{-}$个反例，根据，此时真正例率和假正例率均为0，在坐标(0,0)标记一个点。然后，将分类阈值依次设为每个样例的预测值，即依次将每个样例划分为正例。设前一个标记点坐标为(x,y)，当前若为真正例，则对应标记点的坐标为（x，y+$\frac{1}{m^{+}}$）;当前若为假正例，则对应的标记点坐标为(x+$\frac{1}{m^{-}}$,y),然后连线。
  学习器比较时，同样那根曲线在上面，哪个学习器的优。但是任然存在相交的情况，但是我们一定要进行比较，则较为合理的判据是比较ROC曲线下的面积，即AUC。
  从定义可知，AUC可通过对ROC曲线下部分的面积求和得到。假设ROC曲线是由坐标为{（$x_1,y_1$）,（$x_2,y_2$）,…,（$x_m,y_m$）}点按序链接而生成（$x_1=0,x_m$=1）,b图。则ACU可以估算为：
$$AUC=\frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)\cdot (y_i+y_{i+1})$$
  形式的看AUC考虑的是样本预测的排序质量，因此它与排序误差有紧密联系。给定$m^{+}$个正例和$m^{-}$个反例，令$D^{+}$和$D^{-}$分别表示正例，反例集合，则排序"损失"定义为：
$$lrank=\frac{1}{m^{+}{m}^{-}}\sum _{x_{+}\in D^{+}}\sum _{x_{-}\in D^{-}}(\left|\right|(f(x^{+})<f(x^{-}))+\frac{1}{2}\left|\right|(f(x^{+})=f(x^{-})))$$
  即考虑一个正例,反例,正例预测值小于反例，记一个罚分，相等就0.5个罚分。如果对应的是ROC曲线之上的面积：若一个正例在ROC曲线之上对应的坐标为(x,y)，则x恰是排序在其之前的反例所占比例。有：
$$AUC=1-lrank$$
总结：
  这里需要我们一起来，头脑中回想一下什么是误差？过拟合欠拟合的定义？为了评估学习器的优劣，有哪些方法？性能量度有哪些呢？文章有点长，大家梳理一下吧。