Information Bottleneck【IB】
预备知识
交叉熵损失函数(CrossEntropy Loss)
在DL中,交叉熵损失函数是用作分类问题的,使用它作为Loss Function时,在模型的输出层总会接一个softmax函数。交叉熵是信息论中的一个重要概念,主要时用来度量两个概率分布函数之间的差异性,理解交叉熵之前,需要先了解下面几个概念。
信息量
信息量用来消除随机不确定性的东西,也就是说衡量信息量的大小就是看该消息消除不确定性的程度。例如:
- “CSDN是中国研发的”,这条信息没有减少不确定性,因为CSDN是中国研发的,这是一句废话,信息量为0。
- “JDG能进入四强(2022)”,从直觉上看,这条信息量很大,因为JDG进入四强的不确定因素很大,这句话消除了进入四强的不确定因素,所以这句话信息量很大。
根据上面两条,可以总结为:信息量的大小与信息发生的概率成反比。即,概率越大,信息量越小;概率越小,信息量越大。 设 某一事件发生的概率为P(x),其信息量表示为:
I ( x ) = − l o g ( P ( x ) ) I(x) = - log(P(x)) I(x)=−log(P(x))
其中I(x)表示信息量。
注:用log函数的目的,以2为底时可以简单理解为用多少个bits可以表示这个变量。 用负号是因为0≤p(x)≤1,而信息量是≥0的。
信息熵
信息熵用来表示所有信息量的期望。期望是试验中每次可能结果的概率乘以其信息量的总和。所以信息量的熵可以表示为:
H ( x ) = − ∑ i = 1 n P ( x i ) l o g ( P ( x i ) ) ( X = x 1 , x 2 , . . . , x n ) H(x) = - \sum_{i=1}^nP(x_i) log(P(x_i)) (X = x_1,x_2,...,x_n) H(x)=−i=1∑nP(xi)log(P(xi))(X=x1,x2,...,xn)
相对熵(KL散度)
如果对于同一个随机变量X有两个单独的概率分布P(x) 和Q(x),则我们可以使用KL散度来衡量这两个概率分布之间的差异。
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g ( p ( x i ) q ( x i ) ) D_{KL}(p||q) = \sum_{i=1}^np(x_i) log(\frac {p(x_i)} {q(x_i)}) DKL(p∣∣q)=i=1∑np(xi)log(q(xi)p(xi))
在ML中,常用P(x)来表示样本的真实分布,Q(x)来表示模型所预测的分布,比如在一个三分类的任务中, x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3分别代表猫、狗、马,例如一张马的图片实际真实分布P(X) = [1, 0, 0],预测分布Q(X) = [0.7,0.2,0.1],计算KL散度:
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g ( p ( x i ) q ( x i ) ) = p ( x 1 ) l o g ( p ( x 1 ) q ( x 1 ) + p ( x 2 ) l o g ( p ( x 2 ) q ( x 2 ) + p ( x 3 ) l o g ( p ( x 3 ) q ( x 3 ) = 1 ∗ l o g ( 1 0.7 ) = 0.36 D_{KL}(p||q) = \sum_{i=1}^np(x_i) log(\frac {p(x_i)} {q(x_i)}) = p(x_1)log(\frac {p(x_1)} {q(x_1)} + p(x_2)log(\frac {p(x_2)} {q(x_2)} + p(x_3)log(\frac {p(x_3)} {q(x_3)} = 1 * log(\frac 1 {0.7}) = 0.36 DKL(p∣∣q)=i=1∑np(xi)log(q(xi)p(xi))=p(x1)log(q(x1)p(x1)+p(x2)log(q(x2)p(x2)+p(x3)log(q(x3)p(x3)=1∗log(0.71)=0.36
KL散度越小,表示P(x) 和Q(x)的分布越接近,通过反复训练Q(x)可以使得Q(x)的分布逼近P(x)。
交叉熵
交叉熵 = 信息熵+KL散度
H ( p , q ) = − ∑ i = 1 n p ( x i ) l o g ( p ( x i ) ) + D K L ( p ∣ ∣ q ) = − ∑ i = 1 n p ( x i ) l o g ( p ( x i ) ) + ∑ i = 1 n p ( x i ) l o g ( p ( x i ) q ( x i ) ) = − ∑ i = 1 n p ( x i ) l o g ( q ( x i ) ) H(p,q) = - \sum_{i=1}^np(x_i) log(p(x_i)) + D_{KL}(p||q) = - \sum_{i=1}^np(x_i) log(p(x_i)) + \sum_{i=1}^np(x_i) log(\frac {p(x_i)} {q(x_i)}) = - \sum_{i=1}^np(x_i) log(q(x_i)) H(p,q)=−i=1∑np(xi)log(p(xi))+DKL(p∣∣q)=−i=1∑np(xi)log(p(xi))+i=1∑np(xi)log(q(xi)p(xi))=−i=1∑np(xi)log(q(xi))
注:在分类问题中常常用交叉熵作为loss function,而在线性回归问题中,常常用MSE作为loss function。
- 交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布于预测概率分布之间的差异。交叉熵的值越小,概率预测效果就越好。
- 交叉熵在分类问题常常与softmax一起使用,softmax将输出结果进行处理使得预测值和为1,然后再通过交叉熵来计算损失。
互信息
在信息论中,两个随机变量的互信息或转移信息是变量间相互依赖性的亮度。用I(X;Y)表示。
互信息度量两个随机变量共享的信息——已知随机变量X,对随机变量Y的不确定性减少的程度(已知随机变量Y,对随机变量X的不确定性减少的程度)。听着比较抽象,举着栗子。
随机变量X表示一个均衡的骰子投掷出的点数,Y表示X的奇偶性事件。当X为偶数时,Y=0;当X为奇数时,Y=1.
如果我们知道X=1,则Y=1.(失去Y=0这一信息的可能性,Y的不确定信息减少)
如果我们知道Y=1,则X=1 or X=3 or X=5。(失去X=2,4,6这一信息的可能性,X的不确定信息减少)
下图为互信息的韦恩图:
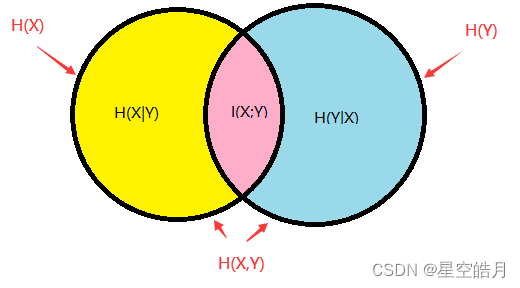
I ( X ; Y ) = H ( x ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) = H ( x ) + H ( Y ) − H ( X , Y ) I(X;Y) = H(x) - H(X|Y) = H(Y) - H(Y|X) = H(x) + H(Y) - H(X, Y) I(X;Y)=H(x)−H(X∣Y)=H(Y)−H(Y∣X)=H(x)+H(Y)−H(X,Y)
其中I(X;Y)表示知道随机变量X,对随机变量Y的不确定性减少的程度,也可表示为随机变量X的不确定性-知道Y的情况下随机变量X的不确定性。H(X),H(Y)表示边缘熵,H(X|Y)和H(Y|X)是条件熵,而H(X,Y)是X和Y的联合熵。
互信息的定义:
I ( X ; Y ) = ∑ y ∈ Y ∑ x ∈ X p ( x , y ) l o g ( p ( x , y ) p ( x ) p ( y ) ) I(X;Y) = \sum_{y∈Y}\sum_{x∈X}p(x, y)log(\frac {p(x,y)} {p(x)p(y)}) I(X;Y)=y∈Y∑x∈X∑p(x,y)log(p(x)p(y)p(x,y))
上述定义是在离散随机变量下,其中p(x,y)是X和Y的联合概率分布函数,而p(x)和p(y)分别是X和Y的边缘概率分布函数。若在连续随机变量的情形下,则把求和换成二重定积分即可.
注:
- 两个互相独立的变量之间的互信息为0.
- 当两个变量互为确定性函数(即,知道X觉得Y的值,反之亦然)时,二者的互信息与他们的熵相同。
- 互信息是非负的(即I(X;Y)≥0),并且是对称的(即I(X;Y) = I(Y;X))
- 点互信息PMI: P M I ( x ; y ) = l o g p ( x , y ) p ( x ) p ( y ) = l o g p ( x ∣ y ) p ( x ) = l o g p ( y ∣ x ) p ( y ) PMI(x;y)=log{\frac {p(x,y)} {p(x)p(y)}} = log{\frac {p(x|y)} {p(x)}} = log{\frac {p(y|x)} {p(y)}} PMI(x;y)=logp(x)p(y)p(x,y)=logp(x)p(x∣y)=logp(y)p(y∣x)
- 可以看出,互信息其实就是对X和Y的所有可能的取值情况的点互信息PMI的加权和,而点互信息只是对其中两个点进行相关性判断。
推导I(X;Y) = H(Y) - H(Y|X)
I ( X ; Y ) = ∑ y ∈ Y ∑ x ∈ X p ( x , y ) l o g ( p ( x , y ) p ( x ) p ( y ) ) = ∑ y ∈ Y ∑ x ∈ X p ( x , y ) l o g ( p ( x , y ) p ( x ) ) − ∑ y ∈ Y ∑ x ∈ X p ( x , y ) l o g p ( y ) = ∑ y ∈ Y ∑ x ∈ X p ( x ) p ( y ∣ x ) l o g p ( y ∣ x ) − ∑ y ∈ Y ∑ x ∈ X p ( x , y ) l o g p ( y ) = ∑ x p ( x ) ( ∑ y p ( y ∣ x ) l o g p ( y ∣ x ) ) − ∑ y l o g p ( y ) ( ∑ x p ( x , y ) ) = − ∑ x p ( x ) H ( Y ∣ X = x ) − ∑ y p ( y ) l o g p ( y ) = − H ( Y ∣ X ) + H ( Y ) = H ( Y ) − H ( Y ∣ X ) I(X;Y) = \sum_{y∈Y}\sum_{x∈X}p(x, y)log(\frac {p(x,y)} {p(x)p(y)}) \\ = \sum_{y∈Y}\sum_{x∈X}p(x, y)log(\frac {p(x,y)} {p(x)}) - \sum_{y∈Y}\sum_{x∈X}p(x, y)logp(y) \\ = \sum_{y∈Y}\sum_{x∈X}p(x)p(y|x)logp(y|x) - \sum_{y∈Y}\sum_{x∈X}p(x, y)logp(y) \\ = \sum_xp(x)(\sum_yp(y|x)logp(y|x)) - \sum_ylogp(y)(\sum_xp(x, y)) \\ = -\sum_xp(x)H(Y|X=x) - \sum_yp(y)logp(y) \\ = -H(Y|X) + H(Y) = H(Y) - H(Y|X) I(X;Y)=y∈Y∑x∈X∑p(x,y)log(p(x)p(y)p(x,y))=y∈Y∑x∈X∑p(x,y)log(p(x)p(x,y))−y∈Y∑x∈X∑p(x,y)logp(y)=y∈Y∑x∈X∑p(x)p(y∣x)logp(y∣x)−y∈Y∑x∈X∑p(x,y)logp(y)=x∑p(x)(y∑p(y∣x)logp(y∣x))−y∑logp(y)(x∑p(x,y))=−x∑p(x)H(Y∣X=x)−y∑p(y)logp(y)=−H(Y∣X)+H(Y)=H(Y)−H(Y∣X)
互信息也可表示为两个随机变量的边缘分布X和Y的乘积p(x) * p(y) 相对于随机变量的联合熵p(x, y)的相对熵:
I ( X ; Y ) = D K L ( p ( x , y ) ∣ ∣ p ( x ) p ( y ) ) I(X;Y) = D_{KL}(p(x, y)||p(x)p(y)) I(X;Y)=DKL(p(x,y)∣∣p(x)p(y))
I ( X ; Y ) = ∑ y p ( y ) ∑ x p ( x ∣ y ) l o g ( p ( x ∣ y ) p ( x ) ) = ∑ y p ( y ) D K L ( p ( x ∣ y ) ∣ ∣ p ( x ) ) = E Y D K L ( p ( x ∣ y ) ∣ ∣ p ( x ) ) I(X;Y) = \sum_yp(y)\sum_xp(x|y)log(\frac {p(x|y)} {p(x)}) \\ = \sum_yp(y)D_{KL}(p(x|y)||p(x)) \\ = E_Y{D_{KL}(p(x|y)||p(x))} I(X;Y)=y∑p(y)x∑p(x∣y)log(p(x)p(x∣y))=y∑p(y)DKL(p(x∣y)∣∣p(x))=EYDKL(p(x∣y)∣∣p(x))
注意到,这里相对熵涉及到仅对随机变量X积分,表达式 D K L ( p ( x ∣ y ) ∣ ∣ p ( x ) ) D_{KL}(p(x|y)||p(x)) DKL(p(x∣y)∣∣p(x)),现在已Y 为变量。
互信息也可以理解为相对熵X的单变量分布p(x)相对于给定Y时X的条件分布p(x|y):分布p(x|y)和p(x)之间的平均差异越大,信息增益越大。
信息瓶颈IB
IB理论在深度学习中的应用:IB把DL阶段分为两部分,第一部分是尽可能增加feature和输出特征Y的互信息,第二部分是尽可能压缩输入特征X和中间feature的互信息,使得中间feature包含X最有用的信息。
可以将IB理解为一个损失函数,IB理论吧神经网络理解为一个Encoder和一个Decoder,Encoder将输入X编码成Z,解码器把Z解码成输出Y,而IB理论的目标则是:
R I B ( θ ) = I ( Z , Y ; θ ) − β I ( Z , X ; θ ) R_{IB}(θ) = I(Z,Y;θ) - βI(Z,X;θ) RIB(θ)=I(Z,Y;θ)−βI(Z,X;θ)
其中
- R I B ( θ ) R_{IB}(θ) RIB(θ)是信息瓶颈,θ是网络的参数(要优化的东西),β是拉格朗日乘子。
- I(Z, Y;θ)是输出Y和中间featureZ的互信息
- I(Z, X;θ)是输入X和中间featureZ的互信息
IB理论的本质就是:最大化输出特征Y和中间featureZ的互信息,尽量减少输入特征X和中间featureZ的互信息。(按照互信息的概念)实际上就是希望Z中尽量减少输入特征X与输出特征Y不相关的信息,保留输入特征X和输出特征Y最相关的信息。
通过论文中的公式推导,可以得到 R I B ( θ ) R_{IB}(θ) RIB(θ)的下界为L,最大化IB相当于最大化L,取L的相反数为 J I B J_{IB} JIB,相当于最小化 J I B J_{IB} JIB。因此可以吧 J I B J_{IB} JIB作为模型的损失函数:
J I B = 1 N ∑ n = 1 N E z ∽ f ( x ) , ϵ [ − l o g q ( y n ∣ z ) ] + β D K L [ p ( z ∣ x n ) ∣ ∣ r ( z ) ] = 1 N ∑ n = 1 N E ϵ ∽ p ( ϵ ) [ − l o g q ( y n ∣ f ( x n , ϵ ) ) ] + β D K L [ p ( z ∣ x n ) ∣ ∣ r ( z ) ] J_{IB}=\frac1 N\sum_{n=1}^N\mathbb{E}_{z \backsim f(x),\epsilon }[-logq(y_n|z)] +βD_{KL}[p(z|x_n)||r(z)] \\ =\frac1 N\sum_{n=1}^N\mathbb{E}_{\epsilon \backsim p(\epsilon)}[-logq(y_n|f(x_n, \epsilon))] +βD_{KL}[p(z|x_n)||r(z)] JIB=N1n=1∑NEz∽f(x),ϵ[−logq(yn∣z)]+βDKL[p(z∣xn)∣∣r(z)]=N1n=1∑NEϵ∽p(ϵ)[−logq(yn∣f(xn,ϵ))]+βDKL[p(z∣xn)∣∣r(z)]
其中:
- p ( z ∣ x n ) p(z|x_n) p(z∣xn)为模型的encoder, q ( y n ∣ z ) q(y_n|z) q(yn∣z)为模型的decoder。
信息瓶颈理论实际上是信源压缩的率失真理论的一种扩展。
- 率失真理论:没有先验知识,只有记住,但可以消除数据本身的冗余,是最传统的数据压缩,允许压缩时失真。给定失真下可获得的最低压缩码率,即在失真和压缩码率之间权衡。
- 信息瓶颈理论:有先验知识(数据带标签),消除数据本身冗余外,还压缩与标签无关的信息。在保留与标签相关信息与获得更高效的压缩之间权衡。
The information bottleneck method
在这篇论文中,Tishby从信息论中关于数据压缩的经典率失真定律出发,拓展处信息瓶颈理论。如下图所示。
| 率失真理论 | 信息瓶颈理论 | |
|---|---|---|
| 问题描述 | 在信源X的期望失真小于D的约束下,尽量降低X的码率 | 尽量保留X关于Y的相关信息前提下,降低X的码率 |
| 优化目标 | F [ p ( x , x ^ ) ] = I ( X ; X ^ ) + β < d ( x , x ^ ) > p ( x , x ^ ) F[p(x,\hat x)] = I(X;\hat X) + β<d(x, \hat x)>_{p(x, \hat x)} F[p(x,x^)]=I(X;X^)+β<d(x,x^)>p(x,x^) | L [ p ( x ^ / x ) ] = I ( X ^ ; X ) − β I ( X ^ ; Y ) L[p(\hat x/x)] = I(\hat X;X) - βI(\hat X;Y) L[p(x^/x)]=I(X^;X)−βI(X^;Y) |
| 距离度量 | < d ( x , x ^ ) > p ( x , x ^ ) = ∑ x ∈ X ∑ x ^ ∈ X ^ p ( x , x ^ ) d ( x , x ^ ) <d(x, \hat x)>_{p(x, \hat x)} = \sum_{x∈X}\sum_{\hat x ∈ \hat X}p(x, \hat x)d(x, \hat x) <d(x,x^)>p(x,x^)=∑x∈X∑x^∈X^p(x,x^)d(x,x^) | d ( x , x ^ ) = D K L ( p ( y / x ) / p ( y / x ^ ) ) d(x, \hat x) = D_{KL}(p(y/x)/p(y/ \hat x)) d(x,x^)=DKL(p(y/x)/p(y/x^)) |
| 迭代算法 | Blahut-Arimoto算法 | 扩展Blahut-Arimoto算法 |
可以看出,率失真理论和信息瓶颈理论都是考虑在一定失真前提下,尽量降低对信源编码的码率( X ^ \hat X X^和X的相互信息),β越小所对应的压缩率越高。区别在于:
- 率失真理论:编码时没有考虑关于信源X的外部信息,只关注编码后的 X ^ \hat X X^与相对原始数据X之间的距离,且距离越大,失真越大。
- 信息瓶颈理论:考虑了信源X中蕴含了关于Y的相关信息,因此对失真的定义为 X ^ \hat X X^与外部数据Y之间的互信息(可转换为KL散度计算),且互信息越大,失真越小。因此,信息瓶颈理论可以看作率失真理论的一种特例。
- Blahut–Arimoto 算法:若集合为凸,且距离度量满足特定条件,则交替化最小化算法收敛到最小值。作为一个特例:集合是概率分布,距离度量为KL散度,则该算法为BA算法保证收敛。
信息瓶颈理论解释了以下的DL问题:
- 模型训练的速度往往是开始收敛得很快,越到后面越慢,因为信息压缩花费的时间到后期指数增加了。
- 在样本不足的情况下,DNN往往表现出比预期要好一些的泛化能力,因为压缩I(X;T)使得泛化误差减小了。每压缩一半的bit数,维持相同泛化误差所需的样本数也减半。
- 从低层到高层,使用一些更改结构信息承载能力上限的技巧,可以达到压缩I(X;T)上限的效果。减少神经元个数(包括max pooling以及降维,还有临时性的drop out)、减少离散化数据的枚举数量(包括使用非线性激活函数、归一化、使用argmax),都在一定程度上减小了泛化误差。
- 无论是SGD还是dropout引入到网络中的噪音/不确定性,都增加了对应那一层的熵H(X|Ti(Wi-1),导致在训练过程中,I(X;T)被进一步压缩。当信号噪声比变小时,也就是训练到了中后期,随机熵导致的压缩会非常明显。然后当收敛趋于停止时,压缩效果也随之减弱,最终哪怕时间指数增加了,压缩量也会逐渐减小。
- 增加神经网络层数可以加快收敛速度,因为每一层随机权重都在进行信息压缩,相当于对噪音导致的信息压缩过程开了多线程。
- 每上升一层神经网络特征,因为信息压缩的现象,所以信息承载上限最好也随之降低,超出所需的I(X;T)比特数,并不会帮助提升预测效果,只会拖累计算速度。有时候需要借助结构改变来减少信息承载上限,从而强制进行不同层间的信息压缩。
- 当I(Y;X) < H(Y)的时候,Y存在X无法描述的固有随机性,存在准确率上限,无论任何模型训练得再完美,都无法让准确率超过这个上限。
- 训练收敛后,如果是能够比较好预测的模型,I(Y;Ti)在每一层都会比较接近于H(Y),这样假设无论从那一层切开,中间重新输入特征值T代替原本的输入X,都能够准确预测出Y。这为逐层解析DNN的特征值含义,提供了一扇分析的窗口。
参考
交叉熵损失函数原理详解
互信息(Mutual Information)
互信息
Information Bottleneck信息瓶颈理论
信息瓶颈理论-笔记