优化和深度学习
优化算法的目标函数通常是基于训练数据集的损失函数,因此优化的目标是减少训练误差。
深度学习中的优化挑战
1.局部最小值
深度学习模型的目标函数通常有许多局部最优解。当优化问题的数值解接近局部最优值时,随着目标函数解的梯度接近或变为零,通过最终迭代获得的数值解可能仅使目标函数局部最优,而不是全局最优。只有一定程度的噪声可能会使参数超出局部最小值。事实上,这是小批量随机梯度下降的有利特性之一,在这种情况下,小批量上梯度的自然变化能够将参数从局部极小值中移出。
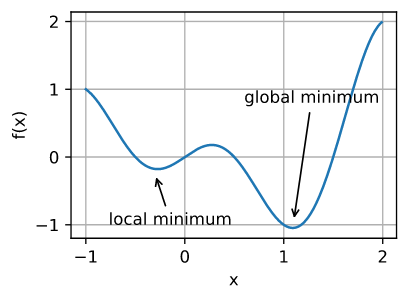
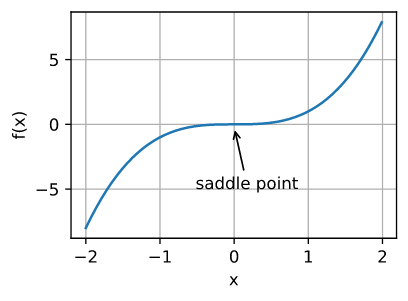
2.鞍点
鞍点(saddle point)是指函数的所有梯度都消失但既不是全局最小值也不是局部最小值的任何位置。
Hessian矩阵:设有凸函数f(X),X是向量(x1,x2,…, xn),Hessian矩阵M定义为:一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,也就是说M的第i行,第j列元素为df(X)/dxidxj, 即为f(X)对于变量xi和xj的二次偏导数。
当函数在零梯度位置处的Hessian矩阵的特征值全部为正值时,我们有该函数的局部最小值。
当函数在零梯度位置处的Hessian矩阵的特征值全部为负值时,我们有该函数的局部最大值。
当函数在零梯度位置处的Hessian矩阵的特征值为负值和正值时,我们对函数有一个鞍点。
对于高维度问题,至少部分特征值为负的可能性相当高。这使得鞍点比局部最小值更有可能。简而言之,凸函数是Hessian函数的特征值永远不是负值的函数。
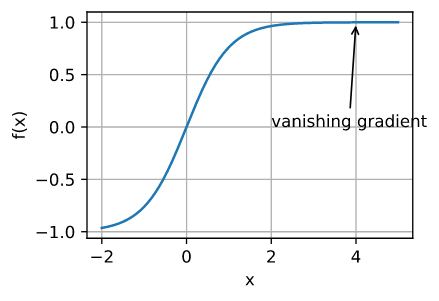
梯度消失
这时候梯度接近于0
凸性
虽然深度学习中的优化问题通常是非凸的, 它们也经常在局部极小值附近表现出一些凸性。
这一节看书吧。。