问题描述:
二十六道二次方程,共二十个未知数。
考虑了matlab中可用的各类算法,最后采用fsolve函数解该复杂非线性方程。
参考:非线性方程(组):MATLAB内置函数 solve, vpasolve, fsolve, fzero, roots [MATLAB] - GentleMin - 博客园

一、使用fsolve最简单函数求解:
将具体的方程定义为root.m文件
用fsolve函数最简单的形式进行求解,x0采用实际模拟结果替代。
myfun = @test_root0426;
x0 = [……];
x = fsolve(myfun,x0)运行结果出现问题:
1.输入参数位数太小,数量级基本在10的-5次方以下,matlab显示不全
通过format long命令,获得长位数结果
2.无法运行获得结果,代码错误
x0 = [……];
root(x0)可以通过在root.m文件下输入如下命令,进行单独运行。如果root.m能够成功计算,说明问题出现在主文件main.m下,对主文件进行检查即可。
报错Solver stopped prematurely.检查原因是main.m中变量定义遗漏。
3.调整部分联动数值后,发现计算结果没有改变。计算结果与初值过于接近,且初值改变,计算结果也随之改变。
发现是由于fsolve函数的特性,初值对其影响很大。

原因是fsolve本身使用的算法:优化方法,即用优化方法求解函数距离零点最近,具体方法为信赖域方法。包含预处理共轭梯度(PCG)、狗腿(dogleg)算法和Levenberg-Marquardt算法等。
共轭梯度法(Conjugate Gradient)是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。 在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
梯度下降,是利用梯度参数方法,通过对数据进行不断拟合,给出一堆Y和x,求解最逼近真实参数w,λ的过程。
最速下降法:最速梯度下降法解决的问题是无约束优化问题,而所谓的无约束优化问题就是对目标函数的求解,没有任何的约束限制的优化问题。
求解这类的问题可以分为两大类:一个是最优条件法和迭代法。
1.最优条件法
最优条件法是是指当函数存在解析形式,能够通过最优性条件求解出显式最优解。对于无约束最优化问题,如果f(x)在最优点x附近可微,那么x是局部极小点的必要条件为: 我们常常就是通过这个必要条件去求取可能的极小值点,再验证这些点是否真的是极小值点。当上式方程可以求解的时候,无约束最优化问题基本就解决了。实际中,这个方程往往难以求解。
2.迭代法

由以上计算步骤可知,最速下降法迭代终止时,求得的是目标函数驻点的一个近似点。
其中确定最优步长tk的方法如下:

选取迭代方向,也就是从当前点迭代的方向。这里选取当前点的梯度负方向,是因为梯度的负方向是局部下降最快的方向。
需要指出的是,某点的负梯度方向,通常只是在该点附近才具有这种最速下降的性质。
在一般情况下,当用最速下降法寻找极小点时,其搜索路径呈直角锯齿状(如下图),在开头 几步,目标函数下降较快;但在接近极小点时,收敛速度长久不理想了。特别适当目标函数的等值 线为比较扁平的椭圆时,收敛就更慢了。

牛顿法
牛顿法的基本思想是利用迭代点xk处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法的速度相当快,而且能高度逼近最优值。基本牛顿法是一种是用导数的算法,它每一步的迭代方向都是沿着当前点函数值下降的方向。但是,基本牛顿法初始点需要足够“靠近”极小点,否则,有可能导致算法不收敛。
二、提高fsolve函数计算精度
myfun = @root;
options = optimoptions('fsolve','Display','iter','MaxFunEvals',10000);
x0 = [……];
[x,fval,exitflag,output] = fsolve(myfun,x0,options)
sum(sum(fval.*val))通过options展示matlab使用fsolve函数的计算过程

1.迭代过程
Iteration-迭代次数
Func-count
First-Order optimality一阶最优性(正常应该逐渐收敛到0,可以看到此处不收敛)
一阶最优性用于度量点 x 与最优点的接近程度。
3.2 The First-Order Optimality Condition
- 一阶最优性度量必须至少为零。
- 一阶最优性等于零的点不一定是最小值。
与一阶最优性相关的停止规则
OptimalityTolerance 容差与一阶最优性度量相关。通常,如果一阶最优性度量小于 OptimalityTolerance,则求解器迭代结束。
一些求解器或算法使用相对一阶最优性作为停止条件。如果一阶最优性度量小于 μ 乘以 OptimalityTolerance,则求解器迭代结束;其中 μ 为:
- 目标函数在
x0处的梯度的无穷范数(最大值) - 求解器的输入的无穷范数(最大值),例如
linprog中的f或b或者quadprog中的H
2.计算结果
另外还有一个参数是exitflag,它表示了fsolve的退出条件。

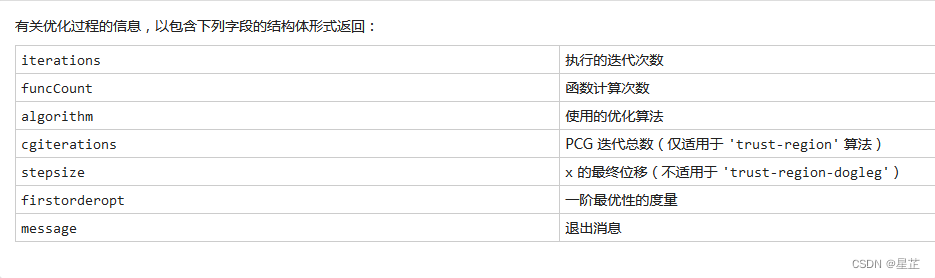
exitflag = 0
output = 包含以下字段的 struct: iterations: 96 funcCount: 3007 algorithm: 'trust-region-dogleg' firstorderopt: 8.3426e+13 message: 'Solver stopped prematurely.↵↵fsolve stopped because it exceeded the function evaluation limit,↵options.MaxFunctionEvaluations = 3.000000e+03.' MaxFunctionEvaluations = 3.000000 e + 03。
ans = 3.7817e+15
ans是sum(sum(fval.*fval))的计算结果,代表残差,正常应该在10的-10次方范围。 此算例中明显不合理。
fval 输出给出函数值 F(x),该值在解处应为零(在 FunctionTolerance 容差内)
3.迭代超限
message: 'Solver stopped prematurely.↵↵fsolve stopped because it exceeded the function evaluation limit,↵options.MaxFunctionEvaluations = 1.000000e+04.’
message: 'Solver stopped prematurely.↵↵fsolve stopped because it exceeded the function evaluation limit,↵options.MaxFunctionEvaluations = 1.000000e+05.’
options = optimoptions('fsolve','Display','iter','MaxFunEvals',100000,'MaxIterations',10000);
过程中会出现各类报错如最大计算值超出,迭代次数超出等,可以用options中的函数修改其上限。
4.优化计算结果
这里是利用梯度下降法,在root.m文件中输出x命令,拿到x的值,将其作为新的x0输入main.m中。通过此方法可以获得收敛的解。
exitflag =
2
output =
包含以下字段的 struct:
iterations: 7
funcCount: 248
algorithm: 'trust-region-dogleg'
firstorderopt: 0.001564384898955
message: 'Equation solved, solver stalled.↵↵fsolve stopped because the relative size of the current step is less than the↵value of the step size tolerance squared and the vector of function values↵is near zero as measured by the value of the function tolerance.↵↵<stopping criteria details>↵↵fsolve stopped because the relative norm of the current step, 3.624206e-13, is less than ↵max(options.StepTolerance^2,eps) = 1.000000e-12. The sum of squared function values,↵r = 2.955544e-06, is less than sqrt(options.FunctionTolerance) = 1.000000e-03.'
ans =
2.955543540610292e-06
且残差值较小,但由于本项目所用的数值都在该数量级附近,因此该误差还是太大,无法满足要求。
重复迭代无法优化残差。
有朋友提到,可以通过矩阵输入多个x0,提高其准确性,但效果不太好。
接下来可能尝试solver进行继续尝试。