一、概述

我们将使用代码（Python/Numpy 等）进行编码，以更好的理解从数据预处理的基础知识到深度学习中使用到的技术。

将从数据科学和机器学习/深度学习中基本但非常有用的概念开始，例如方差和协方差矩阵，我们将进一步介绍一些用于将图像输入神经网络的预处理技术。使用具体代码了解每个方程的作用！

在将原始数据输入机器学习或深度学习算法之前，我们称其为对原始数据的所有转换进行预处理。例如，在原始图像上训练卷积神经网络可能会导致较差的分类性能。预处理对于加快训练也很重要（例如，居中和缩放技术等）。

二、方差和协方差

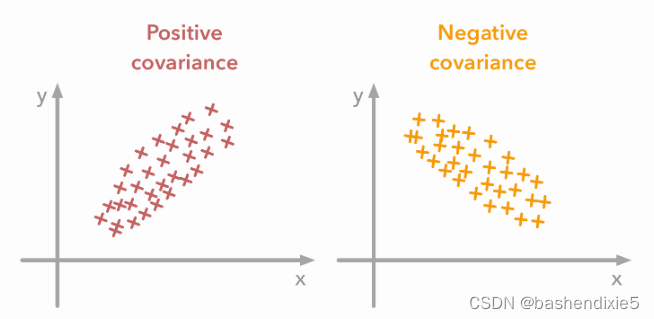
变量的方差描述了值的分布程度。协方差是一种衡量两个变量之间依赖程度的度量。正协方差意味着当第二个变量的值也很大时，第一个变量的值很大。负协方差意味着相反：一个变量的大值与另一个变量的小值相关联。协方差值取决于变量的规模，因此很难对其进行分析。可以使用更容易解释的相关系数。它只是标准化的协方差。

正协方差意味着一个变量的大值与另一个变量的大值相关联（左）。负协方差意味着一个变量的大值与另一个变量的小值相关联（右）。

协方差矩阵是一个矩阵，它集合了一组向量的方差和协方差，它可以告诉你关于变量的很多事情。对角线对应于每个向量的方差：

方差计算公式如下

$V(\boldsymbol{X}) = \frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2$

其中 n 是向量的长度， $\bar{x}$ 是向量的平均值。例如，A 的第一列向量的方差为：

$V(\boldsymbol{A}_{:,1}) = \frac{(1-3)^2+(5-3)^2+(3-3)^2}{3} = 2.67$

这是我们协方差矩阵的第一个单元格。对角线上的第二个元素对应于 A 的第二个列向量的方差，依此类推。

注意：从矩阵 A 中提取的向量对应于 A 的列。

其他单元格对应于来自 A 的两个列向量之间的协方差。例如，第一列和第三列之间的协方差位于协方差矩阵中，即第 1 列和第 3 行（或第 3 列和第 1 行） .

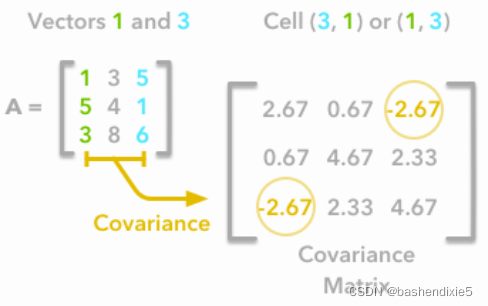
协方差矩阵中的位置。列对应于第一个变量，行对应于第二个（或相反）。 A 的第一列向量和第三列向量之间的协方差是第 1 列和第 3 行中的元素（或相反 = 相同的值）。

让我们确认 A 的第一列向量和第三列向量之间的协方差是否等于 -2.67。两个变量 X 和 Y 之间的协方差公式为：

$cov(\boldsymbol{X},\boldsymbol{Y}) = \frac{1}{n} \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})$

变量 X 和 Y 是上一个示例中的第一个和第三个列向量。让我们拆分这个公式：

1、 $(x_1-\bar{x})$ 求和符号即需要迭代向量的元素。我们将从第一个元素 (i=1) 开始，计算 X 的第一个元素减去向量 X 的平均值。

2、 $(x_1-\bar{x})(y_1-\bar{y})$ 将结果乘以 Y 的第一个元素减去向量 Y 的平均值。

3、 $\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})$ 对向量的每个元素重复该过程并计算所有结果的总和。

4、 $\frac{1}{n} \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})$ 除以向量中的元素数。

1、例1

有如下矩阵 $\boldsymbol{A}= \begin{bmatrix} 1 & 3 & 5 \\ 5 & 4 & 1 \\ 3 & 8 & 6 \end{bmatrix}$ ，我们将计算第一列向量和第三列向量之间的协方差：

$\boldsymbol{X} = \begin{bmatrix} 1 \\ 5 \\ 3 \end{bmatrix}$ 和 $\boldsymbol{Y} = \begin{bmatrix} 5 \\ 1 \\ 6 \end{bmatrix}$ ， $\boldsymbol{\bar{x}}=3$ ， $\boldsymbol{\bar{y}}=4$ ， $n=3$ ，所以

$cov(X,Y) = \frac{(1-3)(5-4)+(5-3)(1-4)+(3-3)(6-4)}{3}=\frac{-8}{3}=-2.67$

即协方差矩阵的值。

现在使用 Numpy，可以使用函数 np.cov 计算协方差矩阵。值得注意的是，如果您希望 Numpy 将列用作向量，则必须使用参数 rowvar=False。此外，bias=True 允许除以n而不是n-1。

A = np.array([[1, 3, 5], [5, 4, 1], [3, 8, 6]])
np.cov(A, rowvar=False, bias=True)

计算结果

array([[ 2.66666667,  0.66666667, -2.66666667],
       [ 0.66666667,  4.66666667,  2.33333333],
       [-2.66666667,  2.33333333,  4.66666667]])

2、例2

还有另一种计算 A 的协方差矩阵的方法，用点积求协方差矩阵。您可以将 A 以 0 为中心（将向量的平均值减去向量的每个元素），将其乘以它的自己的转置并除以观察次数。让我们从一个实现开始，然后我们将尝试理解与前面等式的联系：

def calculateCovariance(X):
    meanX = np.mean(X, axis = 0)
    lenX = X.shape[0]
    X = X - meanX
    covariance = X.T.dot(X)/lenX
    return covariance

让我们在矩阵 A 上对其进行计算：

calculateCovariance(A)

计算结果

array([[ 2.66666667,  0.66666667, -2.66666667],
       [ 0.66666667,  4.66666667,  2.33333333],
       [-2.66666667,  2.33333333,  4.66666667]])

与例1的结果相同。

两个向量之间的点积可以表示为： $\boldsymbol{X^\text{T}Y}= \sum_{i=1}^{n}(x_i)(y_i)$

然后除以向量中元素的数量n： $\frac{1}{n}\boldsymbol{X^\text{T}Y}= \frac{1}{n}\sum_{i=1}^{n}(x_i)(y_i)$

您可以注意到，这与我们在上面看到的协方差公式很像：

$cov(\boldsymbol{X},\boldsymbol{Y}) = \frac{1}{n} \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})$

唯一的区别是，在协方差公式中，我们将向量的平均值减去它的每个元素。这就是为什么我们需要在进行点积之前将数据居中。

现在如果我们有一个矩阵 A，A 和它的转置之间的点积会得到一个新的矩阵：

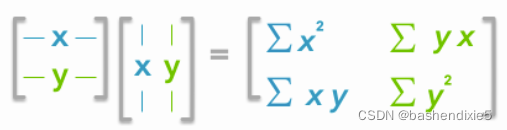
这是协方差矩阵！

三、数据和协方差矩阵可视化

为了更深入地了解协方差矩阵及其用途，我们将创建一个用于将其与 2D 数据一起可视化的函数。您将能够看到协方差矩阵和数据之间的联系。

正如我们在上面看到的，这个函数将计算协方差矩阵。它将创建两个子图：一个用于协方差矩阵，一个用于数据。Seaborn的heatmap函数用于创建颜色渐变：较小的值将被着色为浅绿色，较大的值将被着色为深蓝色。数据表示为散点图。我们选择我们的调色板颜色之一，但您可能更喜欢其他颜色。

def plotDataAndCov(data):
    ACov = np.cov(data, rowvar=False, bias=True)
    print 'Covariance matrix:\n', ACov

    fig, ax = plt.subplots(nrows=1, ncols=2)
    fig.set_size_inches(10, 10)

    ax0 = plt.subplot(2, 2, 1)

    # Choosing the colors
    cmap = sns.color_palette("GnBu", 10)
    sns.heatmap(ACov, cmap=cmap, vmin=0)

    ax1 = plt.subplot(2, 2, 2)

    # data can include the colors
    if data.shape[1]==3:
        c=data[:,2]
    else:
        c="#0A98BE"
    ax1.scatter(data[:,0], data[:,1], c=c, s=40)

    # Remove the top and right axes from the data plot
    ax1.spines['right'].set_visible(False)
    ax1.spines['top'].set_visible(False)

现在我们有了绘图函数，我们将生成一些随机数据来可视化协方差矩阵可以告诉我们的内容。我们将从使用 Numpy 函数np.random.normal()从正态分布中提取的一些数据。

1、不相关数据

该函数需要分布的均值、标准差和观测数作为输入。我们将创建两个随机变量，包含 300 个观测值，标准差为 1。第一个的平均值为 1，第二个的平均值为 2。如果我们从正态分布中抽取两次 300 个观测值，则两个向量将不相关。

np.random.seed(1234)
a1 = np.random.normal(2, 1, 300)
a2 = np.random.normal(1, 1, 300)
A = np.array([a1, a2]).T
A.shape

注意 1：我们转置数据是.T因为原始形状是 (2, 300)，并且我们希望观察的数量为行（因此形状为 (300, 2)）。

注 2：我们使用相同的随机数和np.random.seed函数来重现性。

让我们检查一下数据的样子：

array([[ 2.47143516,  1.52704645],
       [ 0.80902431,  1.7111124 ],
       [ 3.43270697,  0.78245452],
       [ 1.6873481 ,  3.63779121],
       [ 1.27941127, -0.74213763],
       [ 2.88716294,  0.90556519],
       [ 2.85958841,  2.43118375],
       [ 1.3634765 ,  1.59275845],
       [ 2.01569637,  1.1702969 ],
       [-0.24268495, -0.75170595]])

我们有两列向量。

现在，我们可以检查分布是否正常：

sns.distplot(A[:,0], color="#53BB04")
sns.distplot(A[:,1], color="#0A98BE")
plt.show()
plt.close()

我们可以看到分布具有相同的标准差，但均值不同（1 和 2）。所以这正是我们所要求的！

现在我们可以用我们的函数绘制我们的数据集及其协方差矩阵：

plotDataAndCov(A)
plt.show()
plt.close()

结果如下

Covariance matrix:
[[ 0.95171641 -0.0447816 ]
 [-0.0447816   0.87959853]]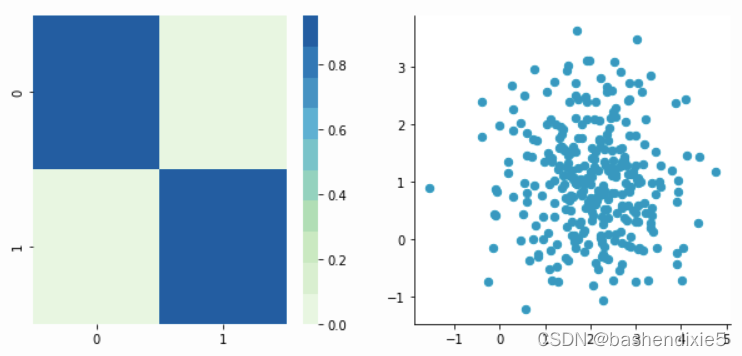

我们可以在散点图上看到这两个维度是不相关的。请注意，我们有一个维度的平均值为 1，而另一个维度的平均值为 2。此外，协方差矩阵显示每个变量的方差非常大（大约为 1），而第 1 列和第 2 列的协方差非常小（约 0）。由于我们确保这两个向量是独立的，因此这是一致的（相反不一定正确：协方差为 0 并不能保证独立性。

2、相关数据

现在，让我们通过从另一列中指定一列来构造依赖数据。

np.random.seed(1234)
b1 =  np.random.normal(3, 1, 300)
b2 = b1 + np.random.normal(7, 1, 300)/2.
B = np.array([b1, b2]).T
plotDataAndCov(B)
plt.show()
plt.close()

数据生成如下

Covariance matrix:
[[ 0.95171641  0.92932561]
 [ 0.92932561  1.12683445]]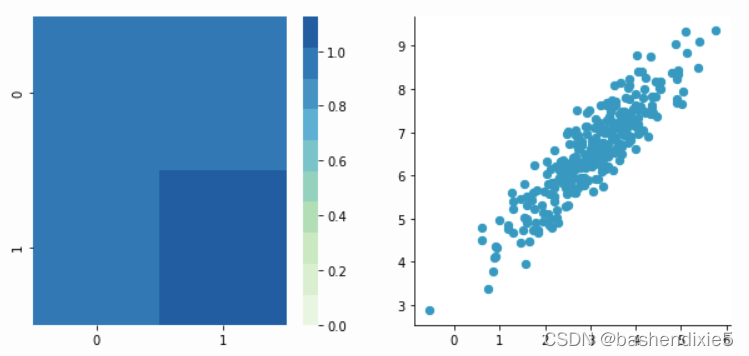

两个维度之间的相关性在散点图上可见。我们可以看到可以绘制一条线并用于从 x 预测 y，反之亦然。协方差矩阵不是对角线（对角线之外有非零单元格）。这意味着维度之间的协方差不为零。

四、预处理

1、均值归一化

均值归一化只是从每个观察数据中删除均值。

$\boldsymbol{X'} = \boldsymbol{X} - \bar{x}$ ，其中 X′ 是归一化数据集，X 是原始数据集， $\bar{x}$ 是 X 的平均值。

它将具有使数据以 0 为中心的效果。我们将创建函数 center() 实现：

def center(X):
    newX = X - np.mean(X, axis = 0)
    return newX

让我们尝试一下我们在上面创建的矩阵 B：

BCentered = center(B)

print 'Before:\n\n'

plotDataAndCov(B)
plt.show()
plt.close()

print 'After:\n\n'

plotDataAndCov(BCentered)
plt.show()
plt.close()

结果如下

Before:

Covariance matrix:
[[ 0.95171641  0.92932561]
 [ 0.92932561  1.12683445]]

After:

Covariance matrix:
[[ 0.95171641  0.92932561]
 [ 0.92932561  1.12683445]]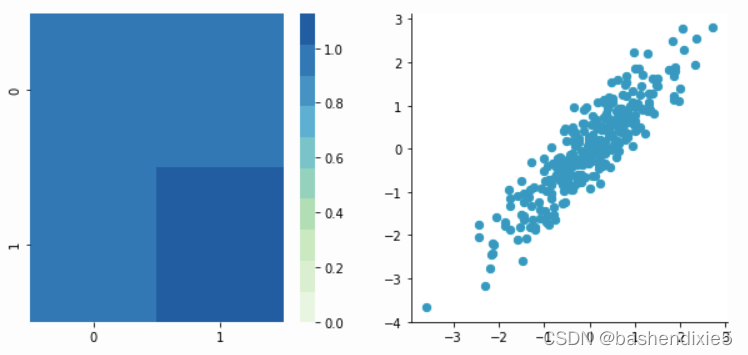

第一个图再次显示原始数据 B，第二个图显示居中的数据（查看x、y坐标进行对比）。

2、标准化

标准化用于将所有特征放在同一尺度上。这样做的方法是将每个以零为中心的维度除以其标准偏差。 $\boldsymbol{X'} = \frac{\boldsymbol{X} - \bar{x}}{\sigma_{\boldsymbol{X}}}$ 其中 X′ 是标准化数据集，X 是原始数据集，x¯ 是 X 的平均值，σX 是 X 的标准差。

def standardize(X):
    newX = center(X)/np.std(X, axis = 0)
    return newX

让我们创建另一个具有不同比例的数据集来检查它是否正常工作。

np.random.seed(1234)
c1 =  np.random.normal(3, 1, 300)
c2 = c1 + np.random.normal(7, 5, 300)/2.
C = np.array([c1, c2]).T

plotDataAndCov(C)
plt.xlim(0, 15)
plt.ylim(0, 15)
plt.show()
plt.close()

结果如下

Covariance matrix:
[[ 0.95171641  0.83976242]
 [ 0.83976242  6.22529922]]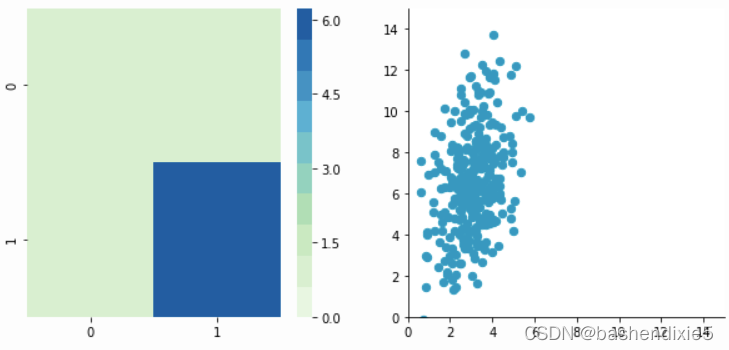

我们可以看到 x 和 y 的尺度是不同的。另请注意，由于规模差异，相关性似乎更小。现在让我们对其进行标准化：

CStandardized = standardize(C)

plotDataAndCov(CStandardized)
plt.show()
plt.close()

结果如下

Covariance matrix:
[[ 1.          0.34500274]
 [ 0.34500274  1.        ]]

现在可以看到比例相同，并且数据集根据两个轴均以零为中心。现在，看一下协方差矩阵：可以看到每个坐标（左上角单元格和右下角单元格）的方差等于1。这个新的协方差矩阵实际上是相关矩阵。两个变量（c1 和 c2）之间的 Pearson 相关系数为 0.54220151。

3、白化

白化或球形数据意味着我们希望以某种方式对其进行转换，以获得一个协方差矩阵，即单位矩阵（对角线为 1，其他单元格为 0；有关单位矩阵的更多详细信息）。它被称为白噪声参考白噪声。

执行白化需要进行以下步骤：

1- 零中心数据
2- 去相关数据
3- 重新调整数据

还是使用上面的矩阵C。

（1）Zero-centering

CCentered = center(C)

plotDataAndCov(CCentered)
plt.show()
plt.close()

Covariance matrix:
[[ 0.95171641  0.83976242]
 [ 0.83976242  6.22529922]]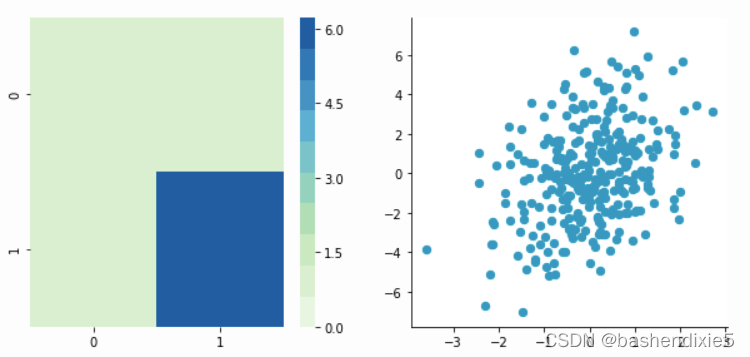

（2）Decorrelate

我们需要对数据进行去相关。直观地说，旋转数据，直到不再有相关性。见下图：

左图显示相关数据。例如，如果你取一个 x 值很大的数据点，那么 y 也很可能会很大。现在获取所有数据点并进行旋转（可能逆时针旋转 45 度左右）：新数据（绘制在右侧）不再相关。

问题是：我们如何才能找到正确的旋转以获得不相关的数据？实际上，这正是协方差矩阵的特征向量所做的：它们指示数据传播最大的方向：

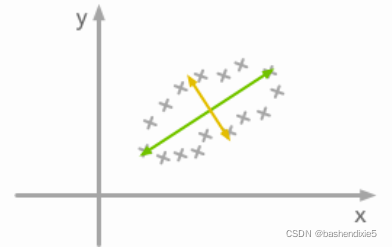
协方差矩阵的特征向量为您提供了使方差最大化的方向。绿线的方向是方差最大的地方。看看这条线上投影的最小和最大点：点差很大。将其与橙色线上的投影进行比较：价差非常小。

所以我们可以通过在特征向量的基础上投影数据来去相关数据。这将产生应用所需的旋转并消除尺寸之间的相关性的效果。以下是步骤：

1-计算协方差矩阵
2-计算协方差矩阵的特征向量
3-将特征向量矩阵应用于数据（这将应用旋转）

让我们创建一个函数：

def decorrelate(X):
    XCentered = center(X)
    cov = XCentered.T.dot(XCentered)/float(XCentered.shape[0])
    # Calculate the eigenvalues and eigenvectors of the covariance matrix
    eigVals, eigVecs = np.linalg.eig(cov)
    # Apply the eigenvectors to X
    decorrelated = X.dot(eigVecs)
    return decorrelated

让我们尝试对我们的以零为中心的矩阵 C 进行去相关，以查看它的实际效果：

plotDataAndCov(C)
plt.show()
plt.close()

CDecorrelated = decorrelate(C)
plotDataAndCov(CDecorrelated)
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.show()
plt.close()

Covariance matrix:
[[ 0.95171641  0.83976242]
 [ 0.83976242  6.22529922]]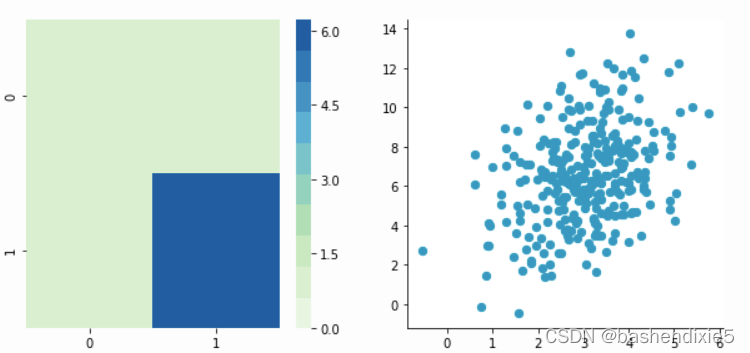

Covariance matrix:
[[  5.96126981e-01  -1.48029737e-16]
 [ -1.48029737e-16   3.15205774e+00]]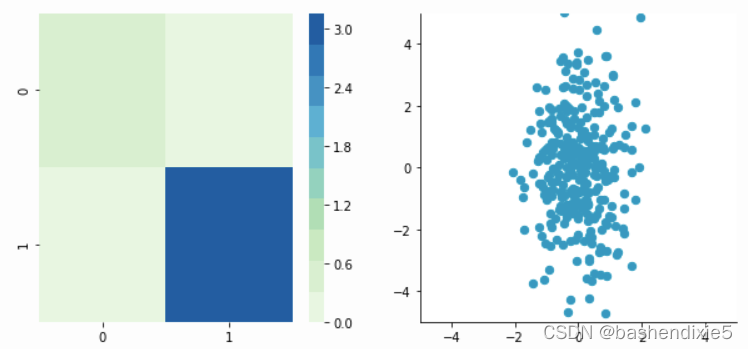

我们可以看到相关性不再存在，并且协方差矩阵（现在是对角矩阵）证实了两个维度之间的协方差等于 0。

（3）Rescale the data

下一步是缩放不相关矩阵以获得对应于单位矩阵的协方差矩阵（对角线上的矩阵和其他单元格上的零）。为此，我们通过将每个维度除以其相应特征值的平方根来缩放我们的去相关数据。

def whiten(X):
    XCentered = center(X)
    cov = XCentered.T.dot(XCentered)/float(XCentered.shape[0])
    # Calculate the eigenvalues and eigenvectors of the covariance matrix
    eigVals, eigVecs = np.linalg.eig(cov)
    # Apply the eigenvectors to X
    decorrelated = X.dot(eigVecs)
    # Rescale the decorrelated data
    whitened = decorrelated / np.sqrt(eigVals + 1e-5)
    return whitened

注意：我们添加一个极小值（这里是 $10^{-5}$ ）以避免被 0 除。

CWhitened = whiten(C)

plotDataAndCov(CWhitened)
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.show()
plt.close()

Covariance matrix:
[[  9.99983225e-01  -1.06581410e-16]
 [ -1.06581410e-16   9.99996827e-01]]

五、图像白化

我们了解一下如何将白化应用于预处理图像数据集。为此，我们将使用 Pal & Sudeep (2016) 的论文，其中提供了有关该过程的一些细节。这种预处理技术称为零分量分析 (ZCA)。

查看论文，但这是他们得到的结果：

来自 CIFAR10 数据集的美白图像。 Pal & Sudeep (2016) 论文的结果。显示了原始图像（左）和 ZCA 之后的图像（右）。

首先加载CIFAR数据集。该数据集可从 Keras 获得。

from keras.datasets import cifar10
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
X_train.shape

CIFAR10 数据集的训练集包含 50000 张图像。 X_train 的形状为 (50000, 32, 32, 3)。每个图像为 32 像素 x 32 像素，每个像素包含 3 个维度（R、G、B）。每个值是 0 到 255 之间对应颜色的亮度。

我们将从只选择图像的一个子集开始，比如说 1000：

X = X_train[:1000]
print X.shape

现在我们将重塑数组，使其具有每行一张图像的平面图像数据。每个图像将是 (1, 3072)，因为 32×32×3=3072。因此，包含所有图像的数组将是 (1000, 3072)：

X = X.reshape(X.shape[0], X.shape[1]*X.shape[2]*X.shape[3])
print X.shape

下一步是能够看到图像。 Matplotlib 中的函数 imshow() 可用于显示图像。它需要形状为 (M×N×3) 的图像，所以让我们创建一个函数来重塑图像并能够从形状 (1, 3072) 中可视化它们。

def plotImage(X):
    plt.figure(figsize=(1.5, 1.5))
    plt.imshow(X.reshape(32,32,3))
    plt.show()
    plt.close()

例如，让我们绘制一张我们加载的图像：

plotImage(X[12, :])

我们现在可以实现图像的白化。

1、第一步是重新缩放图像，通过除以 255（像素的最大值）获得范围 [0, 1]。

使用如下公式 $\frac{data - min(data)}{max(data) - min(data)}$ ，这里，最小值是 0，所以： $\frac{data}{max(data)} = \frac{data}{255}$

X_norm = X / 255.
print 'X.min()', X_norm.min()
print 'X.max()', X_norm.max()

X.min() 0.0
X.max() 1.0

2、从所有图像中减去平均值。

一种方法是获取每张图像并从每个像素中删除该图像的平均值（Jarrett 等人，2009）。这个过程背后的直觉是它将每个图像的像素集中在 0 附近。

另一种方法是为每个图像获取我们拥有的 3072 个像素（R、G 和 B 为 32 x 32 像素）中的每一个，然后减去所有图像中该像素的平均值。这称为每像素平均减法。这一次，每个像素将根据所有图像以 0 为中心。当您向网络提供图像时，每个像素都被视为不同的特征。通过每像素均值减法，我们将每个特征（像素）集中在 0 附近。这是常见的处理办法。

我们现在将从我们的 1000 张图像中进行每像素平均减法。我们的数据按照这些维度（图像、像素）进行组织。是 (1000, 3072) 因为有 1000 张图像，32×32×3=3072 像素。因此，可以从第一个轴获得每个像素的平均值：

X_norm.mean(axis=0).shape
X_norm = X_norm - X_norm.mean(axis=0)
X_norm.mean(axis=0)

现在我们要计算以零为中心的数据的协方差矩阵。就像我们在上面看到的，我们可以使用np.cov()Numpy 的函数来计算它。

我们可以从矩阵中计算出两个可能的相关矩阵X：行之间或列之间的相关性。在我们的例子中，矩阵的每一行X是图像，因此矩阵的行对应于观察值，矩阵的列对应于特征（图像像素）。我们想要计算像素之间的相关性，因为白化的目标是消除这些相关性，以使得算法专注于高阶关系。

为此，设置参数Numpy rowvar=False：它将使用列作为变量（或特征）并将行作为观察值。

cov = np.cov(X_norm, rowvar=False)

协方差矩阵的形状应为 3072 x 3072 以表示每对像素之间的相关性（并且有 3072 个像素）：

我们将计算协方差矩阵的奇异值和向量，并使用它们来旋转我们的数据集。

U,S,V = np.linalg.svd(cov)
print np.diag(S)
print '\nshape:', np.diag(S).shape

$diag(\frac{1}{\sqrt{diag(\boldsymbol{S}) + \epsilon}})$ 也是形状 (3072, 3072) 以及 U 和 $\boldsymbol{U^{\text{T}}}$ ，我们还看到 X 的形状为 (1000, 3072)，我们需要将其转置为 (3072, 1000)。因此 $\boldsymbol{X}_{ZCA}$ 的形状为

$(3072, 3072) . (3072, 3072) . (1000, 3072)^{\text{T}} = (3072, 3072) . (3072, 1000) = (3072, 1000)$ 对应于转置后初始数据集的形状。

epsilon = 0.1
X_ZCA = U.dot(np.diag(1.0/np.sqrt(S + epsilon))).dot(U.T).dot(X_norm.T).T

让我们重新缩放图像：

X_ZCA_rescaled = (X_ZCA - X_ZCA.min()) / (X_ZCA.max() - X_ZCA.min())
print 'min:', X_ZCA_rescaled.min()
print 'max:', X_ZCA_rescaled.max()

最后，我们可以通过对比一张白化前后的图像来看看白化的效果：

看起来像 Pal & Sudeep (2016) 论文中的图像。他们使用 epsilon = 0.1。我们可以尝试其它值以查看对图像的影响。

机器学习笔记 - 深度学习的预处理和图像白化

一、概述

二、方差和协方差

1、例1

2、例2

三、数据和协方差矩阵可视化

1、不相关数据

2、相关数据

四、预处理

1、均值归一化

2、标准化

3、白化

（1）Zero-centering

（2）Decorrelate

（3）Rescale the data

五、图像白化

猜你喜欢