目录
1、简介
图的定义:图是一种描述和分析实体间关系或相互作用的通用语言。

图神经网络有以下两种方法来定义图上的卷积:

2、内容
一、图模型定义
以下是一个图的例子,邻接矩阵表明了图中各个节点的连接关系,度矩阵是邻接矩阵按行或按列相加。我们假设每一个节点有四个属性,比如1-6号节点的属性分别为:[1,1,1,1],...,[6,6,6,6],节点属性的集合组成属性矩阵X。
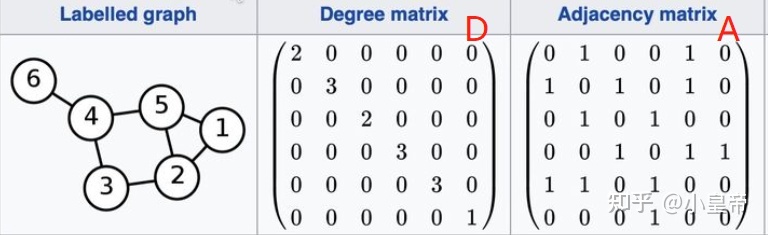
将邻接矩阵和属性矩阵相乘可以有如下结果:

所得结果可以看作是下一层各个结点的属性信息,可见下一层该节点的属性中是包含了上一层该节点相邻节点的属性信息。但是这样会有两个问题:
问题一:下一层该节点结合了上一层该节点周围相邻节点信息,但是并没有结合自身信息。
解决办法:A = A + I,其中I为单位矩阵,相当于邻接矩阵对角线上元素为1。
问题二:经过AX相乘,结果越来越大,多层之后结果会与输入越来越大。
解决办法:对邻接矩阵进行归一化,数学表示为:度矩阵的逆乘邻接矩阵,例子如下:

实际用到的邻接矩阵归一化操作是:![]() ,这样处理的好处和之后引入的Laplacian Matrix有关。
,这样处理的好处和之后引入的Laplacian Matrix有关。

经过以上步骤可以得到图神经网络的传递函数为:
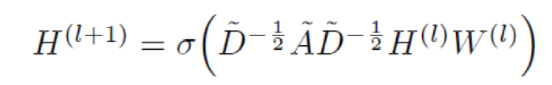
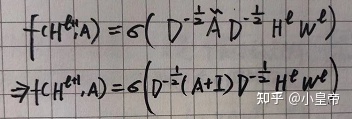
二、图的Laplacian矩阵
表示图的结构可以有多种方式,可以用Adjacency matrix,也可用Incidence matrix,一下这个例子用节点间有指向性的Incidence matrix来描述图的结构。
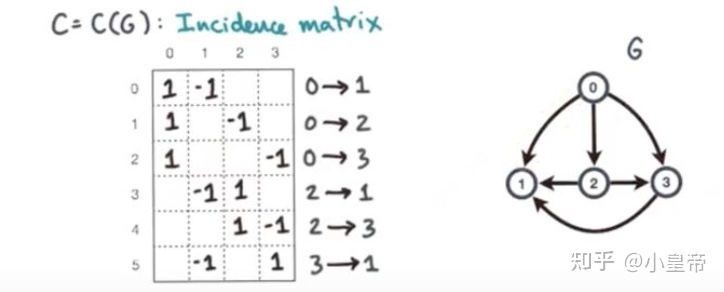
图中1表示边的起点,-1表示边的终点,将这个矩阵记为C。则图的拉普拉斯矩阵记为:
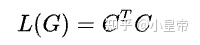
具体有如下结果:

由结果可以发现:主对角线上的值为度,其余位置是邻接矩阵的负值,且行加和或者列加和是0,由此将拉普拉斯矩阵定义为:
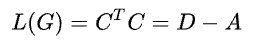
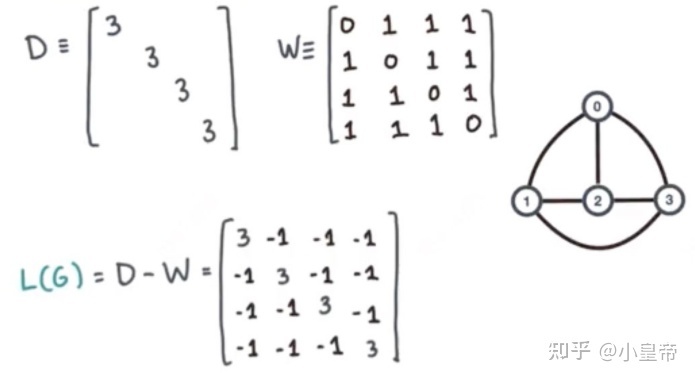
Laplacian矩阵是一个半正定的(特征值>=0)、实对称矩阵,一定可以通过Sihmidt正交化得到单位且相互正交的特征向量和对应的特征值。
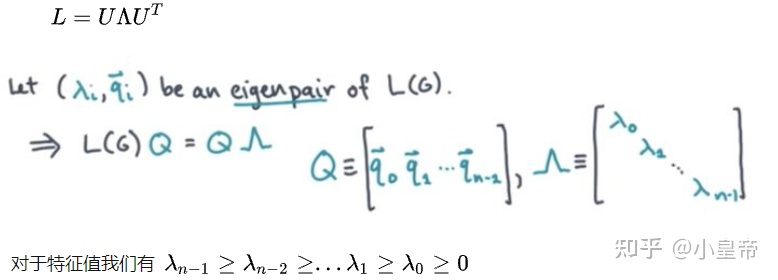
将Laplacian矩阵进行对称归一化:
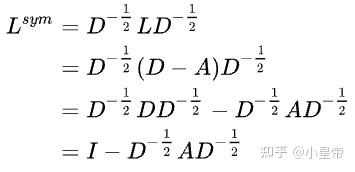
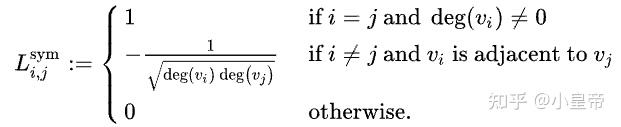
这里引入图傅里叶变换的基:
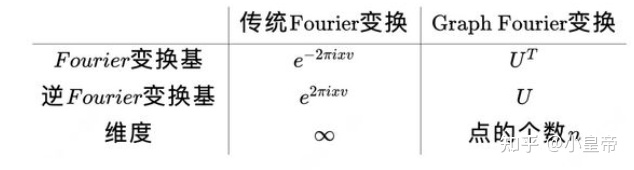
图傅里叶变换的基是图Laplacian矩阵的特征向量,频率可以理解为对应的特征值。给一个直观的例子就是:Laplacian矩阵第一行乘以一个全1的列向量,相当于对Laplacian矩阵第一行求和,那肯定为零。也就是Laplacian矩阵有一个特征值为1,对应一个全1 的特征向量,这就说明,频率为0,信号为1没有波动,是一个将特征值理解为基频率的例子。
三、信号在谱域的傅里叶变换(节点域和谱域的相互转换)
定义节点信号的图傅里叶变换为:
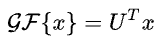
则节点信号的图傅里叶变换的逆变换为:

图傅里叶变换的卷积定理:

注意,这里所有的U都是从图的Laplacian矩阵计算得到的。
我们可以认为x是网络(或者各层)的输入信号,接下来理解节点信号g(filter)如何对x进行卷积。我们希望g可以像CNN的卷积核一样,提取中心点以及它附近的节点区域信息(但该谱方法实现的是全局的信息整合)。
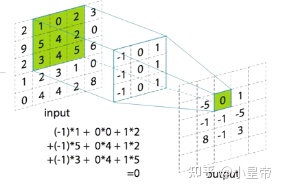
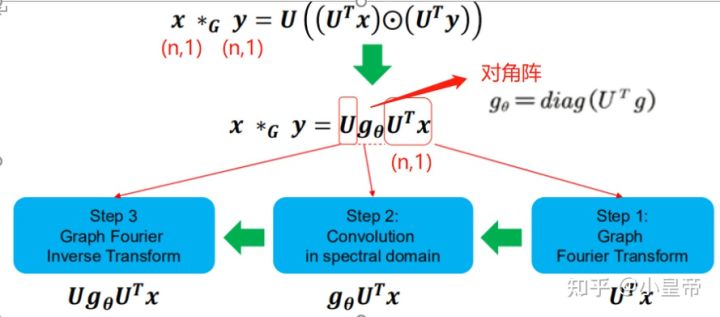
先将输入信号x经过图傅里叶变换转换到谱域,然后谱域中做一次参数化的卷积,在反变换回节点域,完成卷积的定义。g表示不同的卷积核,不同的g提取不同的特征,是待学习参数,与CNN不同的是,这里的g是谱域的参数,而不是原空间的参数。
将信号维度延申,整个卷积过程如下:
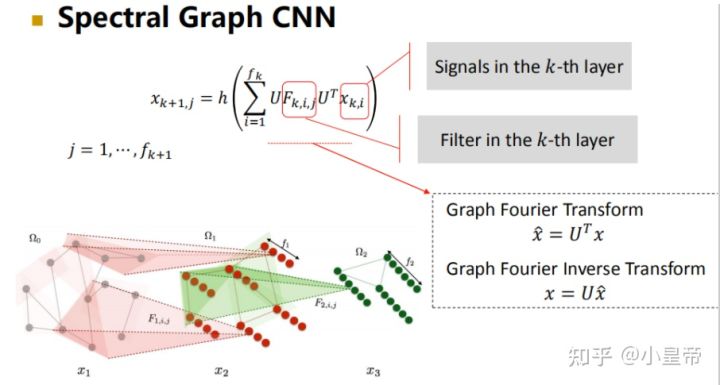
以上过程存在的问题如下:
1、需要显式的求出U,实际计算非常困难。
2、即使算出来了U,它去和x计算,计算复杂度为:O(n**2)。
3、与这个节点做卷积的时候,并不是与它的邻域做的,而是全局做的。
四、谱方法的改进
对于谱方法定义图上卷积的改进主要是针对上述的三点缺点进行改进。
1、ChebyNet:
因为之前的卷积核g自由参数量是n个,很高,改进方法为将g替换为关于Laplacian矩阵的多项式来近似,参数量变为k。


这样处理的好处:
1、特征分解不需要了。
2、L是系数阵,里面有多少不为零的数与网络中的边有关,计算复杂度:O(|E|)。
3、卷积是局部的而不是全局的。L的k次方,相当于使用的是一阶邻接。
2、CWNN(Graph wavelet neural network图小波神经网络):
ChebyNet改进的是g这一部分,将自由度从n降为k。CWNN则致力于U的处理,将傅里叶的基处理为小波的基。

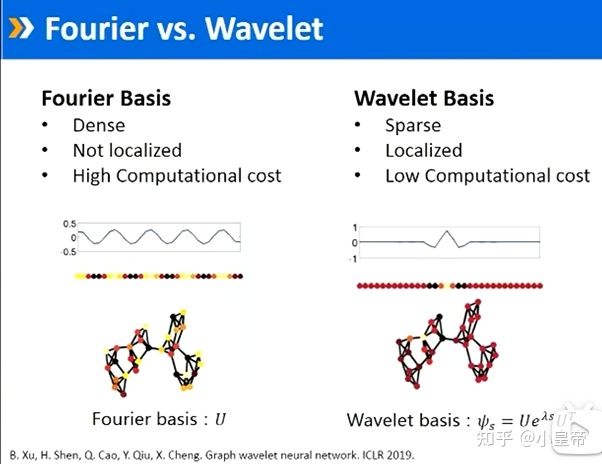
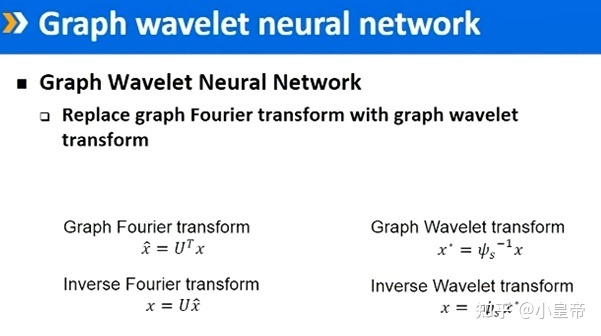

将傅里叶基换为小波基以后,公式中将对应部分替代即可,得到图小波神经网络。
因为参数量大,所以将卷积和特征变换结构拆开。