图论 Graph Theory
1. 基本概念 Basic Concept
- 无向图 & 有向图〔Undirected Graph & Deriected Graph〕
有向图也完全可以实现无向图和混合图,因此有向图的研究一直是重点考察对象。本文讲的所有图都是有向图。
前面提到了我们用连接两点的线表示相应两个事物间具有这种关系。因此如果两个事物间的关系是有方向的,就是有向图,否则就是无向图。比如:A 认识 B,那么 B 不一定认识 A。那么关系就是单向的,我们需要用有向图来表示。因为如果用无向图表示,我们无法区分 A 和 B 的边表示的是 A 认识 B 还是 B 认识 A。
习惯上,我们画图的时候用带箭头的表示有向图,不带箭头的表示无向图。
- 有权图 & 无权图〔Weighted Graph & Unweighted Graph〕
如果边是有权重的是有权图(或者带权图),否则是无权图(或不带权图)。那么什么是有权重呢?比如汇率就是一种有权重的逻辑图。1 货币 A 兑换 5 货币 B,那么我们 A 和 B 的边的权重就是 5。而像朋友这种关系,就可以看做一种不带权的图。
- 入度 & 出度〔Indegree & Outdegree〕
有多少边指向节点 A,那么节点 A 的入度就是多少。同样地,有多少边从 A 发出,那么节点 A 的出度就是多少,下图的出度和入度均为1.

- 路径 & 环〔路径:Path〕
有环图〔Cyclic Graph〕 上面的图就是一个有环图,因为我们从图中的某一个点触发,能够重新回到起点。这和现实中的环是一样的。
无环图〔Acyclic Graph〕
我可以将上面的图稍加改造就变成了无环图,此时没有任何一个环路。

- 连通图 & 强连通图
在无向图中,若任意两个顶点 i 与 j 都有路径相通,则称该无向图为连通图。
在有向图中,若任意两个顶点 i 与 j 都有路径相通,则称该有向图为强连通图。
- 生成树
一个连通图的生成树是指一个连通子图,它含有图中全部 n 个顶点,但只有足以构成一棵树的 n-1 条边。一颗有 n 个顶点的生成树有且仅有 n-1 条边,如果生成树中再添加一条边,则必定成环。在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树,其中代价和指的是所有边的权重和。
2. 图存储结构 Graph Structure
一般图的题目都不会给你一个现成的图的数据结构。当你知道这是一个图的题目的时候,解题的第一步通常就是建图。上面讲的都是图的逻辑结构,那么计算机中的图如何存储呢?
我们知道图是有点和边组成的。理论上,我们只要存储图中的所有的边关系即可,因为边中已经包含了两个点的关系。这里我简单介绍两种常见的建图方式:邻接矩阵(常用,重要)和邻接表。

- 邻接矩阵
第一种方式是使用数组或者哈希表来存储图,这里我们用二维数组来存储。
使用一个 n * n 的矩阵来描述图 graph,其就是一个二维的矩阵,其中 graphi 描述边的关系。
一般而言,对于无权图我都用 graphi = 1 来表示 顶点 i 和顶点 j 之间有一条边,并且边的指向是从 i 到 j。用 graphi = 0 来表示 顶点 i 和顶点 j 之间不存在一条边。 对于有权图来说,我们可以存储其他数字,表示的是权重。

可以看出上图是对角线对称的,这样我们只需看一半就好了,这就造成了一半的空间浪费。
这种存储方式的空间复杂度为 O(n ^ 2),其中 n 为顶点个数。如果是稀疏图(图的边的数目远小于顶点的数目),那么会很浪费空间。并且如果图是无向图,始终至少会有 50 % 的空间浪费。下面的图也直观地反应了这一点。
邻接矩阵的优点主要有:
- 直观,简单。
- 判断两个顶点是否连接,获取入度和出度以及更新度数,时间复杂度都是 O(1)
- 由于使用起来比较简单, 因此我的所有的需要建图的题目基本都用这种方式。
使用二维数组构建邻接矩阵:
class AdjacencyMatrix(object):
def __init__(self, n, directed = False):
self.n = n # number of vertex
self.m = 0 # number of edge
self.directed = directed
self.matrix = [[0 for i in range(n)] for i in range(n)]
def hasEdge(self, v, w):
if 0 <= v <= self.n and 0 <= w <= self.n:
return self.matrix[v][w]
else:
raise Exception("vertex not in the Graph")
def addEdge(self, v, w):
if 0 <= v <= self.n and 0 <= w <= self.n:
if self.hasEdge(v, w):
return
self.matrix[v][w] = 1
if self.directed is False:
self.matrix[w][v] = 1
self.m += 1
else:
raise Exception("vertex not in the Graph")
- 邻接表
对于每个点,存储着一个链表,用来指向所有与该点直接相连的点。对于有权图来说,链表中元素值对应着权重。
例如在无向无权图中:
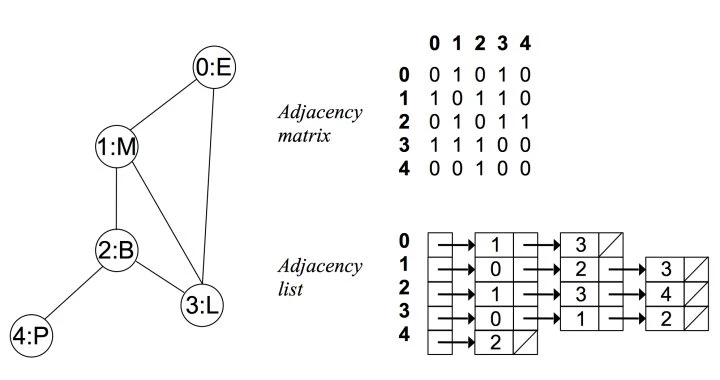
可以看出在无向图中,邻接矩阵关于对角线对称,而邻接链表总有两条对称的边。
而在有向无权图中:
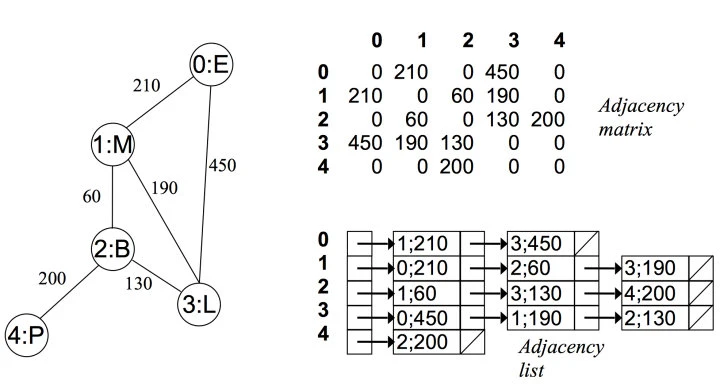
使用字典构建邻接表:
class Vertex(object):
def __init__(self, key):
self.id = key
self.connectedTo = {
}
def addNeighbor(self, nbr, weight=0):
self.connectedTo[nbr] = weight
def getConnection(self):
return self.connectedTo.keys()
class AdjacencyList(object):
def __init__(self, directed=False):
self.vertList = {
}
self.numvert = 0
self.directed = directed
# 添加顶点
def addVertex(self, key):
newVertex = Vertex(key)
self.vertList[key] = newVertex
self.numvert += 1
return newVertex
# 查看是否有该顶点
def getVertex(self, n):
if n in self.vertList:
return self.vertList[n]
else:
return None
# 添加顶点之间的线段
def addEdge(self, frompoint, endpoint, cost=0):
if frompoint not in self.vertList:
newVertex = self.addVertex(frompoint)
if endpoint not in self.vertList:
newVertex = self.addVertex(endpoint)
self.vertList[frompoint].addNeighbor(self.vertList[endpoint], cost)
3. 图的遍历 Graph Traversal
图建立好了,接下来就是要遍历了。
不管你是什么算法,肯定都要遍历的,一般有这两种方法:深度优先搜索,广度优先搜索(其他奇葩的遍历方式实际意义不大,没有必要学习)。
不管是哪一种遍历, 如果图有环,就一定要记录节点的访问情况,防止死循环。当然你可能不需要真正地使用一个集合记录节点的访问情况,比如使用一个数据范围外的数据原地标记,这样的空间复杂度会是 O ( 1 ) O(1) O(1)。
这里以有向图为例, 有向图也是类似,这里不再赘述。
- 深度优先遍历〔Depth First Search, DFS〕
深度优先遍历图的方法是,从图中某顶点 v 出发, 不断访问邻居, 邻居的邻居直到访问完毕。

如上图, 如果我们使用 DFS,并且从 A 节点开始的话, 一个可能的的访问顺序是: A -> C -> B -> D -> F -> G -> E,当然也可能是 A -> D -> C -> B -> F -> G -> E 等,具体取决于你的代码,但他们都是深度优先的。
- 广度优先搜索〔Breadth First Search, BFS〕
广度优先搜索,可以被形象地描述为 “浅尝辄止”,它也需要一个队列以保持遍历过的顶点顺序,以便按出队的顺序再去访问这些顶点的邻接顶点。

如上图, 如果我们使用 BFS,并且从 A 节点开始的话, 一个可能的的访问顺序是: A -> B -> C -> F -> E -> G -> D,当然也可能是 A -> B -> F -> E -> C -> G -> D 等,具体取决于你的代码,但他们都是广度优先的。
需要注意的是 DFS 和 BFS 只是一种算法思想,不是一种具体的算法。 因此其有着很强的适应性,而不是局限于特点的数据结构的,本文讲的图可以用,前面讲的树也可以用。实际上, 只要是非线性的数据结构都可以用。
4. 最短路径 Shortest Path
- Dijkstra 算法
Dijkstra 算法主要解决的是 图中任意一点到图中另外任意一个点的最短距离,即单源最短路径。比如给你几个城市,以及城市之间的距离。让你规划一条最短的从城市 a 到城市 b 的路线。
这个问题,我们就可以先将城市间的距离用图建立出来,然后使用 dijkstra 来做。那么 dijkstra 究竟如何计算最短路径的呢?
dj 算法的基本思想是贪心。从起点 start 开始,每次都遍历所有邻居,并从中找到距离最小的,本质上是一种广度优先遍历。这里我们借助堆这种数据结构,使得可以在 l o g N logN logN 的时间内找到 cost 最小的点。
而如果使用普通的队列的话,其实是图中所有边权值都相同的特殊情况。比如我们要找从点 start 到点 end 的最短距离。我们期望 dj 算法是这样被使用的。
比如一个图是这样的:
E -- 1 --> B -- 1 --> C -- 1 --> D -- 1 --> F
\ /\
\ ||
-------- 2 ---------> G ------- 1 ------
我们使用邻接矩阵来构造:
G = {
"B": [["C", 1]],
"C": [["D", 1]],
"D": [["F", 1]],
"E": [["B", 1], ["G", 2]],
"F": [],
"G": [["F", 1]],
}
shortDistance = dijkstra(G, "E", "C")
print(shortDistance) # E -- 3 --> F -- 3 --> C == 6
具体算法:
初始化堆。堆里的数据都是 (cost, v) 的二元祖,其含义是“从 start 走到 v 的距离是 cost”。因此初始情况,堆中存放元组 (0, start)
从堆中 pop 出来一个 (cost, v),第一次 pop 出来的一定是 (0, start)。 如果 v 被访问过了,那么跳过,防止环的产生。
如果 v 是 我们要找的终点,直接返回 cost,此时的 cost 就是从 start 到 该点的最短距离
否则,将 v 的邻居入堆,即将 (neibor, cost + c) 加入堆。其中 neibor 为 v 的邻居, c 为 v 到 neibor 的距离(也就是转移的代价)。
重复执行 2 - 4 步
import heapq
def dijkstra(graph, start, end):
# 堆里的数据都是 (cost, i) 的二元祖,其含义是“从 start 走到 i 的距离是 cost”。
heap = [(0, start)]
visited = set()
while heap:
(cost, u) = heapq.heappop(heap)
if u in visited:
continue
visited.add(u)
if u == end:
return cost
for v, c in graph[u]:
if v in visited:
continue
next = cost + c
heapq.heappush(heap, (next, v))
return -1
DJ 算法的时间复杂度为 O ( v l o g v + e ) O(vlogv+e) O(vlogv+e),其中 v 和 e 分别为图中的点和边的个数。
- Floyd-Warshall 算法
Floyd-Warshall 可以 解决任意两个点距离,即多源最短路径。相比上面的 dijkstra 算法, 由于其计算过程会把中间运算结果保存起来防止重复计算,因此其特别适合求图中任意两点的距离。
还有一个非常重要的点是 Floyd-Warshall 算法由于使用了动态规划的思想而不是贪心,因此其可以处理负权重的情况。
算法也不难理解,简单来说就是: i 到 j 的最短路径 = i 到 k 的最短路径 + k 到 j 的最短路径的最小值。如下图:

u 到 v 的最短距离是 u 到 x 的最短距离 + x 到 v 的最短距离。上图 x 是 u 到 v 的必经之路,如果不是的话,我们需要多个中间节点的值,并取最小的。该算法的时间复杂度是 O ( N 3 ) O(N^3) O(N3),空间复杂度是 O ( N 2 ) O(N^2) O(N2),其中 N 为顶点个数。
# graph 是邻接矩阵,n 是顶点个数
# graph 形如: graph[u][v] = w
def floyd_warshall(graph, n):
dist = [[float("inf") for _ in range(n)] for _ in range(n)]
for i in range(n):
for j in range(n):
dist[i][j] = graph[i][j]
# check vertex k against all other vertices (i, j)
for k in range(n):
# looping through rows of graph array
for i in range(n):
# looping through columns of graph array
for j in range(n):
if (
dist[i][k] != float("inf")
and dist[k][j] != float("inf")
and dist[i][k] + dist[k][j] < dist[i][j]
):
dist[i][j] = dist[i][k] + dist[k][j]
return dist
- Bellman-Ford 算法
Bellman-Ford 算法主要解决单源最短路径,即图中某一点到其他点的最短距离,其基本思想也是动态规划。
核心算法为:
初始化起点距离为 0
对图中的所有边进行若干次处理,直到稳定。处理的依据是:对于每一个有向边 (u,v),如果 dist[u] + w 小于 dist[v],那么意味着我们找到了一条到达 v 更近的路,更新之。
上面的若干次的上限是顶点 V 的个数,因此不妨直接进行 n 次处理。
最后检查一下是否存在负边引起的环。
举个例子。对于如下的一个图,存在一个 B -> C -> D -> B,这样 B 到 C 和 D 的距离理论上可以无限小。我们需要检测到这一种情况,并退出。
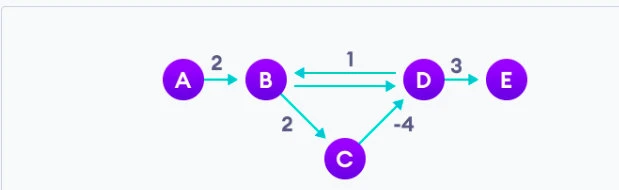
此算法时间复杂度: O ( V ∗ E ) O(V*E) O(V∗E), 空间复杂度: O ( V ) O(V) O(V)。
# return -1 for not exsit
# else return dis map where dis[v] means for point s the least cost to point v
def bell_man(edges, s):
dis = defaultdict(lambda: math.inf)
dis[s] = 0
for _ in range(n):
for u, v, w in edges:
if dis[u] + w < dis[v]:
dis[v] = dis[u] + w
for u, v, w in edges:
if dis[u] + w < dis[v]:
return -1
return dis
5. 拓扑排序 Topological Sorting
在计算机科学领域,有向图的拓扑排序是对其顶点的一种线性排序,使得对于从顶点 u 到顶点 v 的每个有向边 uv, u 在排序中都在之前。当且仅当图中没有定向环时(即有向无环图),才有可能进行拓扑排序。
典型的题目就是给你一堆课程,课程之间有先修关系,让你给出一种可行的学习路径方式,要求先修的课程要先学。任何有向无环图至少有一个拓扑排序。已知有算法可以在线性时间内,构建任何有向无环图的拓扑排序。
- Kahn 算法
简单来说,假设 L 是存放结果的列表,先找到那些入度为零的节点,把这些节点放到 L 中,因为这些节点没有任何的父节点。然后把与这些节点相连的边从图中去掉,再寻找图中的入度为零的节点。对于新找到的这些入度为零的节点来说,他们的父节点已经都在 L 中了,所以也可以放入 L。重复上述操作,直到找不到入度为零的节点。如果此时 L 中的元素个数和节点总数相同,说明排序完成;如果 L 中的元素个数和节点总数不同,说明原图中存在环,无法进行拓扑排序。
def topologicalSort(graph):
"""
Kahn's Algorithm is used to find Topological ordering of Directed Acyclic Graph
using BFS
"""
indegree = [0] * len(graph)
queue = collections.deque()
topo = []
cnt = 0
for key, values in graph.items():
for i in values:
indegree[i] += 1
for i in range(len(indegree)):
if indegree[i] == 0:
queue.append(i)
while queue:
vertex = queue.popleft()
cnt += 1
topo.append(vertex)
for x in graph[vertex]:
indegree[x] -= 1
if indegree[x] == 0:
queue.append(x)
if cnt != len(graph):
print("Cycle exists")
else:
print(topo)
# Adjacency List of Graph
graph = {
0: [1, 2], 1: [3], 2: [3], 3: [4, 5], 4: [], 5: []}
topologicalSort(graph)
6. 最小生成树 Minimum Spanning Tree
首先我们来看下什么是生成树。
首先生成树是原图的一个子图,它本质是一棵树,这也是为什么叫做生成树,而不是生成图的原因。其次生成树应该包括图中所有的顶点。 如下图由于没有包含所有顶点,换句话说所有顶点没有在同一个联通域,因此不是一个生成树。
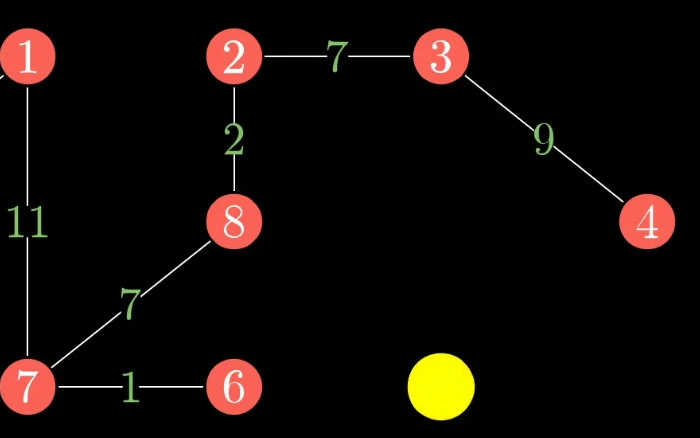
你可以将生成树看成是根节点不确定的多叉树,由于是一棵树,那么一定不包含环。如下图就不是生成树。

因此不难得出,最小生成树的边的个数是 n - 1,其中 n 为顶点个数。
接下来我们看下什么是最小生成树。
最小生成树是在生成树的基础上加了最小关键字,是最小权重生成树的简称。从这句话也可以看出,最小生成树处理正是有权图。生成树的权重是其所有边的权重和,那么最小生成树就是权重和最小的生成树,由此可看出,不管是生成树还是最小生成树都可能不唯一。
最小生成树在实际生活中有很强的价值。比如我要修建一个地铁,并覆盖 n 个站,这 n 个站要互相都可以到达(同一个联通域),如果建造才能使得花费最小?由于每个站之间的路线不同,因此造价也不一样,因此这就是一个最小生成树的实际使用场景,类似的例子还有很多。

计算最小生成树就是从边集合中挑选 n - 1 个边,使得其满足生成树,并且权值和最小。
- Kruskal 算法
Kruskal 算法也被形象地称为加边法,每前进一次都选择权重最小的边,加入到结果集。为了防止环的产生(增加环是无意义的,只要权重是正数,一定会使结果更差),我们需要检查下当前选择的边是否和已经选择的边联通了。如果联通了,是没有必要选取的,因为这会使得环产生。因此算法上,我们可使用并查集辅助完成。
Kruskal 具体算法:
对边按照权值从小到大进行排序。
将 n 个顶点初始化为 n 个联通域
按照权值从小到大选择边加入到结果集,每次贪心地选择最小边。如果当前选择的边是否和已经选择的边联通了(如果强行加就有环了),则放弃选择,否则进行选择,加入到结果集。
重复 3 直到我们找到了一个联通域大小为 n 的子图
class DisjointSetUnion:
def __init__(self, n):
self.n = n
self.rank = [1] * n
self.f = list(range(n))
def find(self, x: int) -> int:
if self.f[x] == x:
return x
self.f[x] = self.find(self.f[x])
return self.f[x]
def unionSet(self, x: int, y: int) -> bool:
fx, fy = self.find(x), self.find(y)
if fx == fy:
return False
if self.rank[fx] < self.rank[fy]:
fx, fy = fy, fx
self.rank[fx] += self.rank[fy]
self.f[fy] = fx
return True
class Solution:
def Kruskal(self, edges) -> int:
n = len(points)
dsu = DisjointSetUnion(n)
edges.sort()
ret, num = 0, 1
for length, x, y in edges:
if dsu.unionSet(x, y):
ret += length
num += 1
if num == n:
break
return ret
- Prim 算法
Prim 算法也被形象地称为加点法,每前进一次都选择权重最小的点,加入到结果集。形象地看就像一个不断生长的真实世界的树。
Prim 具体算法:
初始化最小生成树点集 MV 为图中任意一个顶点,最小生成树边集 ME 为空。我们的目标是将 MV 填充到 和 V 一样,而边集则根据 MV 的产生自动计算。
在集合 E 中 (集合 E 为原始图的边集)选取最小的边 <u, v> 其中 u 为 MV 中已有的元素,而 v 为 MV 中不存在的元素(像不像上面说的不断生长的真实世界的树),将 v 加入到 MV,将 <u, v> 加到 ME。
重复 2 直到我们找到了一个联通域大小为 n 的子图
class Solution:
def Prim(self, dist) -> int:
n = len(dist)
d = [float("inf")] * n # 表示各个顶点与加入最小生成树的顶点之间的最小距离.
vis = [False] * n # 表示是否已经加入到了最小生成树里面
d[0] = 0
ans = 0
for _ in range(n):
# 寻找目前这轮的最小d
M = float("inf")
for i in range(n):
if not vis[i] and d[i] < M:
node = i
M = d[i]
vis[node] = True
ans += M
for i in range(n):
if not vis[i]:
d[i] = min(d[i], dist[i][node])
return ans
KruKal 的算法复杂度是 O ( E l o g E ) O(ElogE) O(ElogE),Prim 的算法时间复杂度为 O ( E + V l o g V ) O(E + VlogV) O(E+VlogV)。因此 Prim 适合适用于稠密图,而 KruKal 则适合稀疏图。
图嵌入 Graph Embedding
图是描述和分析实体之间的通用语言,天然适合应用于地理信息领域。
- 结点级别:结点(氨基酸)+边(氨基酸的接近度) —> 结点结构
- 边级别:结点(用户及物品)+边(用户与物品的交互关系) —> 边存在
- 子图级别:结点(路段)+边(路段之间的连通性) —> 到达的确切时间
- 图级别:结点(原子)+边(化学联系) —> 生产新的分子结构
图结构天然适合应用于地理信息领域,但直接在这种非结构的,数量不定(可能数目非常多),属性复杂的图上进行机器学习/深度学习是很困难的,而如果能处理为向量将非常的方便。但评价一个好的嵌入需要:
- 保持图属性不变,如图的拓扑结构、顶点连接、顶点周围节点等
- 嵌入速度应该与图的大小无关
- 合适的维度以方便做下游任务
图嵌入本身其实是属于表示学习。主要目的是将图中的节点/图表示成低维,实值,稠密的向量形式,使得到的向量能够做进一步的推理,以更好的实现下游任务。图嵌入包括顶点嵌入/图嵌入,嵌入的方法主要有矩阵分解,随机游走和深度学习。
- 矩阵分解:因为从某种程度上图中的各节点关系可以视为稀疏的矩阵,那么基于矩阵分解的方法就可以得到低维的向量。其中常用的矩阵包括普通的邻接矩阵,度矩阵,拉普拉斯矩阵,节点转移概率矩阵,节点属性矩阵等。
- DeepWalk:通过对图随机游走得到一些序列,把序列当句子,利用word2vec就可以得到每一个“词”的向量了。(前提是基于句子某写词的出现和随机游走访问到的节点都服从幂律分布)。
- Graph Neural Network:图神经网络通过结合深度学习来得到图嵌入,图神经网络可以结合矩阵分解
1. DeepWalk
在图中,如果能把节点表示成合适的数值,能做很多任务,例如节点分类,关系预测,聚类等等。如何把节点表示成计算机能看懂的数值目前也有很多方法,本文主要为介绍基于DeepWalk的节点表示方法。
从某个节点的邻居中随机挑选一个节点作为下一跳节点的过程称为随机游走(Random Walk,下文简称游走),多次重复游走过程可产生游走序列。
随机游走负责对图进行采样,获得图中节点与节点的共现关系。产生的序列可以作为训练样本输送到模型(如word2vec)中进行训练,进而得到图上节点嵌入向量,即embedding。
Graph Embedding技术将图中的节点以低维稠密向量的形式进行表达,要求在原始图中相似(不同的方法对相似的定义不同)的节点其在低维表达空间也接近。得到的表达向量可以用来进行下游任务,如节点分类,链接预测,可视化或重构原始图等。虽然DeepWalk是KDD 2014的工作,但却是我们了解Graph Embedding无法绕过的一个方法。在NLP任务中,word2vec是一种常用的word embedding方法,word2vec通过语料库中的句子序列来描述词与词的共现关系,进而学习到词语的向量表示。
DeepWalk的思想类似word2vec,使用图中节点与节点的共现关系来学习节点的向量表示。那么关键的问题就是如何来描述节点与节点的共现关系,DeepWalk给出的方法是使用随机游走(RandomWalk)的方式在图中进行节点采样。
RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。
获取足够数量的节点访问序列后,使用skip-gram model 进行向量学习。
首先根据用户的行为构建出一个图网络;随后通过Random walk随机采样的方式构建出结点序列(例如:一开始在A结点,A->B,B又跳到了它的邻居结点E,最后到F,得到"A->B->E->F"序列);对于序列的问题就是NLP中的语言模型,因为我们的句子就是单词构成的序列。接下来我们的问题就变成Word2vec(词用向量表示)的问题,采用Skip-gram的模型来得到最终的结点向量。可以说这种想法确实是十分精妙,将图结构转化为序列问题确实是非常创新的出发点。在这里,结点走向其邻居结点的概率是均等的。当然,在有向图和无向图中,游走的方式也不一样。无向图中的游走方式为相连即可走;而有向图中则是只沿着“出边”的方向走。

- 图a展示原始的用户行为序列
- 图b基于这些用户行为序列构建了物品相关图,可以看出,物品A,B之间的边产生的原因就是因为用户U1先后购买了物品A和物品B,所以产生了一条由A到B的有向边。如果后续产生了多条相同的有向边,则有向边的权重被加强。在将所有用户行为序列都转换成物品相关图中的边之后(原始的deepwalk paper中是没有权重的,就是randomWalk),得到全局的物品相关图。
- 图c采用随机游走的方式随机选择起始点,对每个节点重新生成部分物品序列(采样)。得到局部相关联的训练数据,deepwalk将这组序列当成语言模型的一个短句,最大化给定短句某个中心词时,出现上下文单词的概率。
- 图d最终将这些物品序列输入word2vec模型,生成最终的物品Embedding向量。
DeepWalk算法

DeepWalk算法主要包括两个步骤:
第一步为随机游走采样节点序列,构建同构网络,从网络中的每个节点开始分别进行Random Walk 采样,得到局部相关联的训练数据;
第二步为使用skip-gram modelword2vec学习表达向量,对采样数据进行SkipGram训练,将离散的网络节点表示成向量化,最大化节点共现,使用Hierarchical Softmax来做超大规模分类的分类器

DeepWalk采用DFS即深度优先遍历
def deepwalk_walk(self, walk_length, start_node):
walk = [start_node]
while len(walk) < walk_length:
cur = walk[-1]
cur_nbrs = list(self.G.neighbors(cur))
if len(cur_nbrs) > 0:
walk.append(random.choice(cur_nbrs))
else:
break
return walk
需要注意的是,DeepWalk中的DFS和数据结构与算法中的dfs思想类似,但是细节存在差异,在deepwalk中游走到死胡同直接break,而数据结构与算法中游走到死胡同返回初始点继续游走
Skip-gram介绍
skip-gram 和 CBOW 是两种 word2vec 算法,前者是通过中间的词预测两边的词,后者是通过周边的词预测中间的词。就实际效果而言,skip-gram 效果更好。skip-gram 的结构如下图所示。

直接用gensim里的Word2Vec
def deepwalk_walk(self, walk_length, start_node):
walk = [start_node]
while len(walk) < walk_length:
cur = walk[-1]
cur_nbrs = list(self.G.neighbors(cur))
if len(cur_nbrs) > 0:
walk.append(random.choice(cur_nbrs))
else:
break
return walk
walks是训练所需语料(Node Embedding Sentences)
1.sg=1是skip-gram算法,对低频词敏感;默认sg=0为CBOW算法。
2.size是输出词向量的维数,值太小会导致词映射因为冲突而影响结果,值太大则会耗内存并使算法计算变慢,一般值取为100到200之间。
3.window是句子中当前词与目标词之间的最大距离,3表示在目标词前看3-b个词,后面看b个词(b在0-3之间随机)。
4.min_count是对词进行过滤,频率小于min-count的单词则会被忽视,默认值为5。
5.negative和sample可根据训练结果进行微调,sample表示更高频率的词被随机下采样到所设置的阈值,默认值为1e-3。
6.hs=1表示层级softmax将会被使用,默认hs=0且negative不为0,则负采样将会被选择使用。
7.workers控制训练的并行,此参数只有在安装了Cpython后才有效,否则只能使用单核。
2. Node2Vec
2016年出现的node2vec,node2vec的思想同DeepWalk一样,生成随机游走,对随机游走采样得到(节点,上下文)的组合,然后用处理词向量的方法对这样的组合建模得到网络节点的表示。不过在生成随机游走过程中做了一些创新,node2vec改进了DeepWalk中随机游走的生成方式(通过调整随机游走权重的方法使graph embedding的结果在网络的同质性(homophily)和结构性(structural equivalence)中进行权衡),使得生成的随机游走可以反映深度优先和广度优先两种采样的特性,从而提高网络嵌入的效果。

node2vec提出在图网络中很多节点往往有一些类似的结构特征。一种结构特征是很多节点会聚集在一起,内部的连接远比外部的连接多,称之为社区。另一种结构特征是网络中两个可能相聚很远的点,在边的连接上有着类似的特征。
网络的“同质性”指的是距离相近节点的embedding应该尽量近似,如图,节点u与其相连的节点s1、s2、s3、s4的embedding表达应该是接近的,这就是“同质性“的体现。
网络的“结构性”指的是结构上相似的节点的embedding应该尽量接近,图中节点u和节点s6都是各自局域网络的中心节点,结构上相似,其embedding的表达也应该近似,这是“结构性”的体现。
node2vec论文中提出一个好的网络表示学习算法的目标必须满足这两点:
- 同一个社区内的节点表示相似。
- 拥有类似结构特征的节点表示相似。
node2vec算法

node2vec游走方式
node2vec的主要创新点通过改进游走方式
- 深度优先游走DFS
- 广度优先搜索BFS
就如上图的标注所示,深度优先游走策略将会限制游走序列中出现重复的结点,防止游走掉头,促进游走向更远的地方进行。而广度优先游走策略相反将会促进游走不断的回头,去访问上一步结点的其他邻居结点。这样一来,当使用广度优先策略时,游走将会在一个社区内长时间停留,使得一个社区内的结点互相成为context,这也就达到了第一条优化目标。相反,当使用深度优先的策略的时候,游走很难在同一个社区内停留,也就达到了第二条优化目标。
复杂网络处理的任务离不开两种特性:一种是同质性,就是上文所说的社区。一种就是结构相似性。广度优先搜索BFS倾向于在初始节点的周围游走,可以反映出一个节点的邻居的微观特性;而深度优先游走DFS一般会跑的离初始节点越来越远,可以反映出一个节点邻居的宏观特性。
node2vec区别于deepwalk,主要是通过节点间的跳转概率。跳转概率是三阶关系,即考虑当前跳转节点,以及前一个节点 到下一个节点的“距离”,通过返回参数p和进出(或叫远离)参数q控制游走的方向(返回还是继续向前)

对于节点v,其下一步要采样的节点x,通过下面的转移概率公式计算
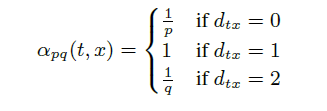
其中d(t, x)代表t结点到下一步结点x的最短路,最多为2。
- 如果t与x相等,那么采样x的概率为 1/p,当d(t, x)=0时,表示下一步游走是回到上一步的结点;
- 如果t与x相连,那么采样x的概率1,当d(t, x)=1时,表示下一步游走跳向t的另外一个邻居结点;
- 如果t与x不相连,那么采样x概率为 1/q,当d(t, x)=2时,表示下一步游走向更远的结点移动。
参数p、q的意义分别如下:
返回概率p:
- 如果 p > max(q,1) p>max(q,1) p>max(q,1) ,那么采样会尽量不往回走,对应上图的情况,就是下一个节点不太可能是上一个节点t。
- 如果 p < max( q,1) p<max(q,1) p<max(q,1) ,那么采样会更倾向于返回上一个节点,这样就会一直在起始点周围某些节点来回转来转去。
出入参数q:
- 如果 q > 1 q>1 q>1,那么游走会倾向于在起始点周围的节点之间跑,可以反映出一个节点的BFS特性。
- 如果 q < 1 q<1 q<1 ,那么游走会倾向于往远处跑,反映出DFS特性。
当p=1,q=1时,游走方式就等同于DeepWalk中的随机游走
四 node2vec和deep walk 捕捉网络什么特性
| BFS随机游走策略产生的embedding结果 | DFS随机游走策略产生的embedding结果 |
|---|---|
 |
 |
颜色接近的节点代表其embedding的相似性更强
BFS的搜索策略非常类似于社区发现所得到的社区相似性,即更加接近一种直观容易解释的思路,偏向于一阶和二阶近邻这类的相似性,也就是距离接近,特别是直接连接的nodes之间的embedding结果接近,也就是“结构性”,可以理解为,BFS的搜索策略能够捕捉到“近邻相似性”;
DFS则看起来不那么直观了,但是其实从传统graph的一些评价指标可以进行分析和总结,例如pagerank,pagerank值计算的是节点的流行度,比如说中国的明星和美国的明星,二者的近邻相似度肯定是非常低的,但是它们都在“演艺圈”这个巨大的graph中扮演着相似的角色,这一点我们可以通过pagerank这类统计方法来得到,成龙和杰森斯坦森之间的pagerank值的差异相对于成龙或杰森斯坦森和其它18线小明星的pagerank值的差异明显要小得多,而我们的dfs捕捉的相似性指的就是这种相似性,即 节点在更大的范围内(可能横跨多个社区而形成的大子图,具体根据random walk的步数来决定)中扮演的角色(同质性,同样性质的相似性),例如我们看第二幅图,连接不同nodes的“枢纽节点”其embedding的相似度往往比较高,从社交网络的角度来说,这些枢纽节点都是“交际花”,虽然她们彼此之间的直接相连的近邻相似度可能非常低,但是它们“交际”的性质是非常相似的,即在局部的子图中扮演着相似的角色;
p和q均为1的时候,node2vec退化为deepwalk,因此实际上我们可以知道,deepwalk本身并不是基于什么dfs之类的做游走的,就是一个纯粹的随机乱走,它即可以捕捉到部分结构性也可以捕捉到部分同质性,具体deepwalk能够捕捉到什么样的性质,就看天意了,所以我们不能说deepwalk就是基于dfs的游走策略游走主要捕捉同质性,而应该说deepwalk同时捕捉两种特性然而两种特性都捕捉的不是非常到位,而node2vec更像是基于deepwalk上的一个灵活的框架,因为我们可以通过指定超参数来改变我们想要进行embedding的目的,如果我们面临的实际问题,定义相似性为同质性,
因此,只能说deepwalk能够捕捉节点之间的共现性,这个共现性可能包含了同质性也可能包含了结构性,而node2vec可以让使用者灵活的定义我们要捕捉更多的结构性还是更多的同质性,置于基于整个graph的同质性,比如上面所说的远距离局部社区相同或者相似角色的embedding问题,我们就需要考虑使用别的embedding算法来解决了,比如计算复杂度非常高基本没法在大规模graph上运行的struc2vec。
3. LINE
采用广度优先搜索策略来生成上下文节点:只有距离给定节点最多两跳的节点才被视为其相邻节点。 此外,与 DeepWalk 中使用的分层 softmax 相比,它使用负采样来优化 Skip-gram 模型。
4. SDNE
直观含义,就是TransE基于实体和关系的分布式向量表示,将每个三元组实例(head,relation,tail)中的关系relation看做从实体head到实体tail的翻译,通过不断调整h、r和t(head、relation和tail的向量),使(h + r) 尽可能与 t 相等,即 h + r = t。
图神经网络 Graph Neural Network
1. 图卷积神经网络 GCN
- 基于谱分解的方法
- 基于空间结构的方法