cmu 16-385 笔记

H* `# image filtering

• Point Operation
  
• Linear shift-invariant image filtering
  
• 2D convolution
  
  如果卷积核可以分解为两个一维卷积核相乘，那么2维卷积也可以分解成两个一维卷积

高斯卷积核

利用梯度来检测边缘，在离散情况下，一维梯度的卷积核可以表示为

和其它不同的一维卷积核组合

Horizontal sober可以在图片中得到许多竖线

gradient direction amplitude 的定义

梯度对噪声非常敏感，所以一般用先用高斯卷积核进行滤波然后再求一阶导数
根据卷积的性质，高斯卷积核可以跟一阶导数结合起来

二阶梯度的卷积核

当二阶梯度(拉普拉斯)卷积核和高斯卷积结合

拉普拉斯可以检测所谓过零点。

image pyramids and frequency domain

aliasing

在下采样过程中造成的信息损失。图中浅色的波是采样前的波，实线是采样后得到的波。

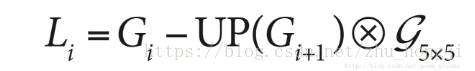
在拉普拉斯金字塔中，从Gi层得到Gi+1层之前首先进行高斯滤波，然后丢弃偶数行和偶数列。然后用Gi减去Gi+1上采样的结果得到第i层的Laplacian images Li。 利用Li可以完美复原图像。

傅里叶变换
一些常见函数及其变换，可以看出傅里叶变换是对称的

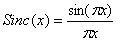
离散傅里叶变换DFT的计算方法
傅里叶变换的 作用是使得两个函数的卷积等于两个函数经过变换后的乘积

采样定律， 只有当采样频率高于两倍Nyquis(尼奎斯特)t频率后才能实现完美复原， 在图像金字塔中，高斯滤波器是一个低通滤波器，可以显著降低Nyquist,从而方便进行下采样。

hough transform

一般情况下已知多个点，求直线的参数使用最小二乘法

但是有两个问题，一个误差函数E有很多方式构建，一个是对噪声点的惩罚很大

扫描二维码关注公众号，回复： 13467854 查看本文章

解决方法是利用hough变换，即把待求参数m和b看做是自变量。 在图像空间中的一个点，到了hough空间后变成了一条线，hough空间中多条直线的交点，对应着图像空间中的一条直线。

找图像空间中直线的方法就是依次找出hough空间中通过最多直线的交点。但是因为直线可以无限延长，所以这种方法很难实现，所以提出一个改进版本，转换成以rho和theta为变脸的函数。因为是周期函数，所以只用考虑0到π。

hough变换还可以扩展到圆上

但是，和求直线时问题一样，a,b,r的测试范围太大。考虑圆上点的性质，过该点切线的垂直线经过圆心，可以利用这一性质来为圆心投票。 垂线的斜率用Gx/Gy表示，Gx是利用sobel算子求出的x方向梯度。

将x轴，y轴，最大半径sqrt(x2+y2) 按照step的间隔划分成若干个离散点，利用这些离散点构成hough空间和并决定投票矩阵vote_matrix的大小。
对于图像中每个像素点，沿着梯度方向寻找候选中心点，并且保持x轴的步长为step。每遍历到一个候选中心点，将其除以step再floor, 转换成hough空间中一个点，并且vote_matrix中的相应值加一。

极大化抑制： 遍历vote_matrix，将其中的点转换回像素空间中的候选中心点（因为转换到hough空间时用了floor操作，所以还原时应该加上step/2）。如果某些点的遍历次数大于阈值，但是他们在像素空间中非常接近，就用一个平均值代替所有的这些点。

class Hough_transform:
    def __init__(self, img, angle, step=5, threshold=135):
        '''

        :param img: 输入的图像
        :param angle: 输入的梯度方向矩阵
        :param step: Hough 变换步长大小
        :param threshold: 筛选单元的阈值
        '''
        self.img = img
        self.angle = angle
        self.y, self.x = img.shape[0:2]
        self.radius = math.ceil(math.sqrt(self.y**2 + self.x**2))
        self.step = step
        self.vote_matrix = np.zeros([math.ceil(self.y / self.step), math.ceil(self.x / self.step), math.ceil(self.radius / self.step)])
        self.threshold = threshold
        self.circles = []

    def Hough_transform_algorithm(self):
        '''
        按照 x,y,radius 建立三维空间，根据图片中边上的点沿梯度方向对空间中的所有单
        元进行投票。每个点投出来结果为一折线。
        :return:  投票矩阵
        '''
        candidate=0;
        print ('Hough_transform_algorithm')
        # ------------- write your code bellow ----------------
        for i in  range(1,self.y-1):
            for j in range(1,self.x-1):
                if self.img[i][j]>0:
                    candidate += 1
                    x=j
                    y=i
                    r=0
                    y_step=self.step*self.angle[i][j]
                    r_step=math.sqrt(self.step**2+ y_step**2)
                    while  x < self.x and y < self.y and x > 0 and y > 0:
                        self.vote_matrix[math.floor(y/self.step)][math.floor(x/self.step)][math.floor(r/self.step)] += 1
                        x+=self.step
                        y+=y_step
                        r+=r_step
                    x=j-self.step
                    y=i-y_step
                    r=r_step
                    while  x < self.x and y < self.y and x > 0 and y > 0:
                        self.vote_matrix[math.floor(y/self.step)][math.floor(x/self.step)][math.floor(r/self.step)] += 1
                        x-=self.step
                        y-=y_step
                        r+=r_step

        # ------------- write your code above ----------------
        print("the number of candidate is %f ",candidate)
        return self.vote_matrix


    def Select_Circle(self):
        '''
        按照阈值从投票矩阵中筛选出合适的圆，并作极大化抑制。
        :return: None
        '''
        print ('Select_Circle')
        # ------------- write your code bellow ----------------
        result=[]
        neighbor=[]
        last_circle=[0,0,0]
        for i in range(0,math.ceil(self.y / self.step)):
            for j in range(0,math.ceil(self.x / self.step)):
                for r in range(0,math.ceil(self.radius / self.step)):
                    if(self.vote_matrix[i][j][r]> self.threshold):
                        y=i*self.step+ self.step / 2
                        x=j*self.step+ self.step / 2
                        rad=r*self.step+ self.step / 2
                        if(len(neighbor)==0 or abs(last_circle[0]-x)+abs(last_circle[1]-y)<20):
                            neighbor.append([x,y,rad])
                            last_circle=[x,y,rad]
                        else:
                            mean=np.array(neighbor).mean(0)
                            neighbor.clear()
                            print("Circle core: (%f, %f)  Radius: %f" % (mean[0],mean[1],mean[2]))
                            self.circles.append([mean[0],mean[1],mean[2]])
        # ------------- write your code above ----------------


    def Calculate(self):
        '''
        按照算法顺序调用以上成员函数
        :return: 圆形拟合结果图，圆的坐标及半径集合
        '''
        self.Hough_transform_algorithm()
        self.Select_Circle()
        return self.circles

canny

cartToPolar 将坐标转换成极坐标。
cv中图片储存的形式为np.zeros([self.y, self.x]，第一维对应y轴。
原理： 先对图像进行高斯平滑。然后利用sobel算子求出每个点梯度的方向以及大小。划分四个大的梯度区间。
梯度区间划分时从-45度到135度划分4个区间分别对应x,y,以及两个对角线。 先沿着梯度方向进行收缩，然后再沿着边缘的方向进行扩张。

class Canny:

    def __init__(self, Guassian_kernal_size, img, HT_high_threshold, HT_low_threshold):
        '''
        :param Guassian_kernal_size: 高斯滤波器尺寸
        :param img: 输入的图片，在算法过程中改变
        :param HT_high_threshold: 滞后阈值法中的高阈值
        :param HT_low_threshold: 滞后阈值法中的低阈值
        '''
        self.Guassian_kernal_size = Guassian_kernal_size
        self.img = img
        self.y, self.x = img.shape[0:2]
        self.angle = np.zeros([self.y, self.x])
        self.img_origin = None
        self.x_kernal = np.array([[-1, 1]])
        self.y_kernal = np.array([[-1], [1]])
        self.HT_high_threshold = HT_high_threshold
        self.HT_low_threshold = HT_low_threshold

    def Get_gradient_img(self):
        '''
        计算梯度图和梯度方向矩阵。
        :return: 生成的梯度图
        '''
        print ('Get_gradient_img')
        # ------------- write your code bellow ----------------
        Gx = cv2.Sobel(self.img, cv2.CV_64F, 1, 0)
        Gy = cv2.Sobel(self.img, cv2.CV_64F, 0, 1)
        gradient_img, self.angle = cv2.cartToPolar(Gx, Gy)
        self.angle = np.tan(self.angle)
        self.img = gradient_img.astype(np.uint8)
        # ------------- write your code above ----------------        
        return self.img

    def Non_maximum_suppression (self):
        '''
        对生成的梯度图进行非极大化抑制，将tan值的大小与正负结合，确定离散中梯度的方向。
        :return: 生成的非极大化抑制结果图
        '''
        print ('Non_maximum_suppression')
        # ------------- write your code bellow ----------------
        result=np.zeros([self.y,self.x])
        for i in range(1,self.y-1):
            for j in range(1,self.x-1):
                if abs(self.img[i][j]) <= 4:
                    result[i][j] = 0
                    continue
                if self.angle[i][j]>1:
                    tmp1 = self.img_origin[i-1][j]
                    tmp2 = self.img_origin[i+1][j]
                elif self.angle[i][j]>0:
                    tmp1 = self.img_origin[i+1][j+1]
                    tmp2 = self.img_origin[i-1][j-1]
                elif self.angle[i][j]>-1:
                    tmp1 = self.img_origin[i][j+1]
                    tmp2 = self.img_origin[i][j-1]
                else:
                    tmp1 = self.img_origin[i-1][j+1]
                    tmp2 = self.img_origin[i+1][j-1]

                if self.img[i][j] >= tmp1 and self.img[i][j] >= tmp2:
                    result[i][j] = self.img[i][j]
                else:
                    result[i][j] = 0
        self.img=result



        # ------------- write your code above ----------------        
        return self.img

    def Hysteresis_thresholding(self):
        '''
        对生成的非极大化抑制结果图进行滞后阈值法，用强边延伸弱边，这里的延伸方向为梯度的垂直方向，
        将比低阈值大比高阈值小的点置为高阈值大小，方向在离散点上的确定与非极大化抑制相似。
        :return: 滞后阈值法结果图
        '''
        print ('Hysteresis_thresholding')
        # ------------- write your code bellow ----------------
        result=np.zeros([self.y,self.x])
        for i in range(1,self.y-1):
            for j in range(1,self.x-1):
                if self.img[i][j] >= self.HT_high_threshold:
                    if self.angle[i][j]>1:
                        if self.img[i][j+1]>self.HT_low_threshold:
                            self.img[i][j+1]=self.HT_high_threshold
                        if self.img[i][j-1]>self.HT_low_threshold:
                            self.img[i][j-1]=self.HT_high_threshold
                    elif self.angle[i][j]>0:
                        if self.img[i+1][j-1]>self.HT_low_threshold:
                            self.img[i+1][j-1]=self.HT_high_threshold
                        if self.img[i-1][j+1]>self.HT_low_threshold:
                            self.img[i-1][j+1]=self.HT_high_threshold
                    elif self.angle[i][j]>-1:
                        if self.img[i+1][j]>self.HT_low_threshold:
                            self.img[i+1][j]=self.HT_high_threshold
                        if self.img[i-1][j]>self.HT_low_threshold:
                            self.img[i-1][j]=self.HT_high_threshold
                    else:
                        if self.img[i + 1][j+1] > self.HT_low_threshold:
                            self.img[i + 1][j+1] = self.HT_high_threshold
                        if self.img[i - 1][j-1] > self.HT_low_threshold:
                            self.img[i - 1][j-1] = self.HT_high_threshold
                elif self.img_origin[i][j] < self.HT_low_threshold:
                    self.img[i][j]=0



        # ------------- write your code above ----------------        
        return self.img

    def canny_algorithm(self):
        '''
        按照顺序和步骤调用以上所有成员函数。
        :return: Canny 算法的结果
        '''
        self.img = cv2.GaussianBlur(self.img, (self.Guassian_kernal_size, self.Guassian_kernal_size), 0)
        self.Get_gradient_img()
        self.img_origin = self.img.copy()
        self.Non_maximum_suppression()
        self.Hysteresis_thresholding()
        return self.img

• Harris
  协方差矩阵$\sum _{i=1}^m{x}^{(i)}{x}^{(i)T}$，这里的x已经经过去中心化。
  假设m个n维数据$(x^{(1)},x^{(2)},...,x^{(m)})$,投影到由$n^{\prime }$个正交基 { w 1 , w 2 , . . . , w n ′ } \{w_1,w_2,...,w_{n'}\} { w1​,w2​,...,wn′​}（用$W$表示）组成的空间上，再把他们复原到n维空间，寻找一个$W$使得原始值和复原值的距离之和最小。$W$应该满足
  $\sum _{i=1}^m{x}^{(i)}{x}^{(i)T}W=\lambda W$ $\lambda$为协方差矩阵最大的$n^{\prime }$个特征值组成的矩阵。

  
  harris算法的基本思想是在图像内找到一个窗口，这个窗口内的像素不管往任何一个移动，灰度的变化都很大
  把E(u，v)整理后可得
  
  

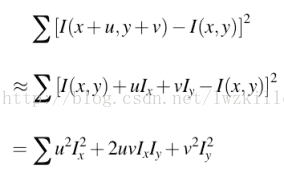
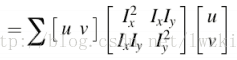
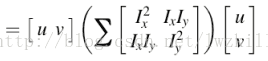
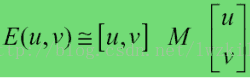
所以对每个窗口的判断转化为对M矩阵的判断，因为要使得不管uv指向哪个方向，E的值都要大，所以要求M矩阵的两个特征值都要大。
直接求特征值肯定是麻烦的，所以可以转向使用度量函数R

• SIFT
  特征检测算子对尺度是敏感的，对拉普拉斯算子的相应只有在特定尺度(半径和sigma对应)下才能达到最大值，可以利用这个特性进行尺度选择。
  
  在尺度选择的时候，用拥有不同sigma并且经过尺度归一化的拉普拉斯算子输出不同尺度下的图片，然后通过每27节点之间的极大化抑制，求出每个点的最佳尺度。每个点可以有多个最佳尺度（尺度特性）。
  高斯核的大小和sigma有一个经验关系，高斯核的宽度差不多是sgima的三倍。一个大的高斯核可以等同于连续使用两个高斯核，例如连续使用两次$\sigma$的高斯核等同于使用一次$\sqrt{2}\sigma$.
  dog （高斯函数差分）算子的波形和高斯拉普拉斯算子（LOG）类似，但是dog可以表示为两个高斯算子的差。DOG和LOG的关系为$G(x,y,k\sigma )-G(x,y,\sigma )\approx (k-1){\sigma }^2{\nabla }^{2}G$，其中${\sigma }^2$是LOG的归一化系数
  并且大的高斯核的计算结果可以在已经计算好的小高斯核的结果的基础上，通过添加另一个小的高斯核得到, 这样可以大大减少提取尺度特征的计算量。比如下一层系数为sig_total, 上一层系数为sig_prev，那么在上一层使用系数为sqrt(sig_totalsig_total - sig_prevsig_prev)的高斯卷积核就能得到下一层。
  
  
  在求出极值点之后，需要剔除其中的边缘点，它们的特点是DOG的海森矩阵不具有各项同性。
  $f(x,y)\approx f(x0,y0)+\left[\begin{array}{ll}\delta x& \delta y\end{array}\right]\left[\begin{array}{l}fx(x0,y0)\\ fy(x0,y0)\end{array}\right]+\frac{1}{2!}\cdot \left[\begin{array}{ll}\delta x& \delta y\end{array}\right]\left[\begin{array}{ll}fxx(x0,y0)& fxy(x0,y0)\\ fyx(x0,y0)& fyy(x0,y0)\end{array}\right]\left[\begin{array}{l}\delta x\\ \delta y\end{array}\right]$
  海森矩阵是多维空间中某一个点的二阶导数，对于曲线来说，二阶导数对应曲率。
  用一个度量函数（和harris算法中的类似）来衡量海森矩阵的各向同性。
  
• keypoint detector 实现
  如果输入图像用uint8保存，那么利用sobel算子求出的梯度可能需要64f保存，在计算完度量函数后，应该转回uint8以节省空间。直接用矩阵的平移来实现每个点和它周围点的比较。
  求出极大值：

  # DOG金字塔中每一个极值点的值应该大于一个阈值，并且度量函数的值小于一个阈值
  contrast_thresh = np.absolute(DoG_pyramid) > th_contrast
  curvature_thresh = np.absolute(principal_curvature) < th_r
  
  # DOG金字塔有三个坐标轴，每个坐标轴的头尾都用0填充
  padded = np.pad(DoG_pyramid, pad_width=1, mode="constant", constant_values=0)
  
  # DOG计算的是梯度，所以值有负有正，需要同时计算极大值和极小值
  compare_max = np.zeros([10, *DoG_pyramid.shape])
  compare_min = np.zeros([10, *DoG_pyramid.shape])
  for c, a, p in [(compare_max, DoG_pyramid, padded), (compare_min, -DoG_pyramid, -padded)]:
      c[0] = a > p[2:, 1:-1, 1:-1] # (x, y, c) > (x+1, y, c)
      c[1] = a > p[2:, 2:, 1:-1] # (x, y, c) > (x+1, y+1, c)
      c[2] = a > p[1:-1, 2:, 1:-1] # (x, y, c) > (x, y+1, c)
      c[3] = a > p[:-2, 2:, 1:-1] # (x, y, c) > (x-1, y+1, c)
      c[4] = a > p[:-2, 1:-1, 1:-1] # (x, y, c) > (x-1, y, c)
      c[5] = a > p[:-2, :-2, 1:-1] # (x, y, c) > (x-1, y-1, c)
      c[6] = a > p[1:-1, :-2, 1:-1] # (x, y, c) > (x, y-1, c)
      c[7] = a > p[2:, :-2, 1:-1] # (x, y, c) > (x+1, y-1, c)
      c[8] = a > p[1:-1, 1:-1, 2:] # (x, y, c) > (x, y, c+1)
      c[9] = a > p[1:-1, 1:-1, :-2] # (x, y, c) > (x, y, c-1)
  
  # Logical AND and OR the local minima and local maxima
  compare = np.logical_or(np.all(compare_max, axis=0), np.all(compare_min, axis=0))
  
  # AND all the conditions
  local_extrema = np.logical_and(np.logical_and(compare, contrast_thresh), curvature_thresh)
  
  # 第一维是坐标轴数量，第二维是极值点数量
  locsDoG = np.array(np.nonzero(local_extrema))
  # 第一维是极值点数量，第二维是坐标轴数量
  locsDoG = np.transpose(locsDoG, (1, 0))
  locsDoG[:,2] = np.array(DoG_levels)[locsDoG[:,2]]
  
  # cv2读取图片后默认第一维是y，第二维是x，但是在
  #cv2.circle函数中圆的坐标值却用(X坐标值，Y坐标值)表示，所以这里做一个转换
  locsDoG[:, [0,1]] = locsDoG[:, [1, 0]]
  
  return locsDoG
  

在得到尺度不变点后，应该在它的附近区域进一步提取特征。 首先根据提取的尺度，画一个圆，然后计算圆内所有点梯度的两个特征值，通过不断的压缩圆，使得两个特征值相同，从而使这个区域具有各向同性。
在对区域内容进行归一化之后，需要对方向也进行归一化。具体方法是用直方图统计各个点的梯度方向和强度，然后旋转直方图中强度最大的方向，使其角度变为0.

接下来是光照强度的不变性， 把选定区域划分成16个小格子， 每个格子用直方图统计梯度强度和方向，最后得到16*8=128维的向量用来描述这个区域。

• 纹理
  在做纹理特征提取的时候，对图像使用48个不同类型，不同尺度，不同方向(对于高斯卷积核(filter bank)来说，意味着协方差不同)的卷积核。然后对于每一个卷积核，对卷积结果的所有像素求平均值。
  

• BRIEF描述子
  多元正态分布,D 是维度
  $P_r=\frac{1}{(2\pi {)}^{D/2}{|\sum |}^{1/2}}\exp \left(-0.5(x-\mu {)}^T{\sum }^{-1}(x-\mu )\right))$
  如果令y=Ax+b，则y的分布为
  $P_r(y)={\mathrm{Norm}}_y\left[A\mu +b,A\sum A^T\right]$
  所以如果想用标准正态分布x采样均值 $\mu$方差为$\sum$的正太分布y，需要令y等于
  ${\sum }^{1/2}x+\mu$

  正态分布中，99.7%的面积这在以期望为中点，以三倍标准差为半径的区间。
  BRIEF是替代梯度直方图的一种方法，优点是计算速度快，缺点是对旋转不鲁棒。

  首先在关键点周围选定一个正方形的patch，然后用按照正态分布采样256个点对，这些点从此就作为一个pattern。 在计算关键点描述向量时，在它的patch遍历按照pattern遍历这些点对，如果点对中的第一个点大于第二个点就向量中对应位置就置1否则为0.

  在sift中，两个描述点之间的差异用欧式距离衡量，所以可以用KDtree来优化最近邻点的检索。构建kdtree的过程：在当前空间找到方差最大的维度，以这个维度的中位数对应的节点为父节点，把当前空间分为左右两个子空间，以此类推
  搜索：把查询节点和各个非叶子节点在对应维度上进行比较，直到找到一个叶子结点（假设属于父节点的左子树），作为当前最近节点，并得到一个当前最小距离。如果当前最佳节点的父节点在对应维度上和查询节点的距离已经超过了当前最小距离，那么就直接跳过右子树，进而回溯到祖父节点。

然而，在brief中使用的是hamming距离,即统计两个向量不同维度的个数，所以直接把所有点对的距离一次性计算出来，并且找出第一幅图中每个关键点在第二幅图中对应的最近邻和第二近邻，如果第一和第二近邻和关键点的距离相差不大(距离之比大于某阈值)则舍弃第一幅图像中的这个关键点。

• brief 特征向量
  以下是提取每个keypoint brief特征的函数，没有使用循环结构。

def computeBrief(im, gaussian_pyramid, locsDoG, k, levels,
    compareX, compareY):
    '''
    Compute brief feature
    INPUT
        locsDoG - locsDoG are the keypoint locations returned by the DoG
                detector.
        levels  - Gaussian scale levels that were given in Section1.
        compareX and compareY - linear indices into the 
                                (patch_width x patch_width) image patch and are
                                each (nbits,) vectors.
    
    
    OUTPUT
        locs - an m x 3 vector, where the first two columns are the image
                coordinates of keypoints and the third column is the pyramid
                level of the keypoints.
        desc - an m x n bits matrix of stacked BRIEF descriptors. m is the number
                of valid descriptors in the image and will vary.
    '''
    
    ##############################
    # TO DO ...
    # compute locs, desc here
    h,w=im.shape
    patch_width=9
    sigma=k
    nbits=compareX.shape[0]
    # 去掉那些因为靠近边界而不能截取patch区域的点
    id_x=np.logical_and(locsDoG[:,0]>patch_width/2,locsDoG[:,0]<w-patch_width/2)
    id_y=np.logical_and(locsDoG[:,1]>patch_width/2,locsDoG[:,1]<h-patch_width/2)

    locsDoG=locsDoG[np.logical_and(id_x,id_y)]


    n_loc=locsDoG.shape[0]
    locs=np.expand_dims(locsDoG[:,0:2],1).repeat(nbits,1)
    im=cv2.GaussianBlur(im,(0,0),sigma)
    compareX=np.expand_dims(compareX,0).repeat(n_loc,0)
    compareY=np.expand_dims(compareY,0).repeat(n_loc,0)

    locs_x=locs+compareX
    locs_y=locs+compareY

    desc=im[(locs_x[:,:,1],locs_x[:,:,0])]<im[(locs_y[:,:,1],locs_y[:,:,0])]

• image stitching
  it’s a task that aimed to warp images to a common coordinate frame
  the common coordinate frame is correspond to the image you pick as the referenced image
  due to the photometric effects such as vignetting（光晕）, there will always be seams in the resulting panorama.
  there is blending algorithm to remove these seams.
  to align two images, we have to find the projective transformation（3 by 3 matrix ）which called homography.
  when matching feature points in two images, there will be outliers, which have similar local appearances but not correspond to the same point in 3d scene. ransac algorithm is used to dealing with these outliers.
• 2D变换
  基本2d变换：
  
  基本2d变换在齐次坐标系下可以转换成3x3矩阵
  在齐次坐标系下对3x3变换矩阵乘以一个常数，不会改变这个变换。
  affine 变换等于uniform sacle(一个自由度)+ shearing + rotation + translation（平移）所以总共6个自由度， 在affine变换中平行的线段会保持平行 即如果转成$\left[\begin{array}{ll}A& \mathbf{t}\\ 0& 1\end{array}\right]$形式，A可以为任意二维矩阵。 仿射变换中线段上的点比例保持不变。

projective transformations 是真实场景中的平面通过小孔映射到图像平面所经历的变换。 如果固定尺度（up to a scale）的话有8个自由度。即在$\left[\begin{array}{ll}A& \mathbf{t}\\ v& 1\end{array}\right]$中添加了v的两个自由度。
线段不一定保持平行，线段之间的比例不一定保持。但是四共线点的交比保持不变。
利用两个图片之间对应的特征点可以计算homography单应性矩阵H，用来计算图像1中的某个坐标 ( u , v )变换到图像2中对应的位置 ( u ′ , v ′ ) , 但是使用H的条件是两个图像的对应区域是同一个平面，但是如果物体离相机很远的话，这个条件可以忽略。

• 计算H
  这里$\alpha$是一个常数，使得等式左边为齐次坐标
  
  装换成一个求解Ah=0的问题，可以看出h乘以任意常数不会改变等式的成立
  
  这里把h当成x,并且加上x模长等于1的限制,注意：使用上面的公式时2，x,y,点是待使用单应性矩阵的点而不是x’,y’
  
  x的值应该为$(A^{T}A)$最小特征根对应的特征向量，而这个特征向量是A（m x n）的奇异值分解$U\Sigma V^T$结果中矩阵V(n x n)的列向量。 奇异值分解用于当A不是方阵时的特征分解。
  因为H的自由度为8，而每一对匹配点点对应两个等式，所以最少需要4对匹配点来计算H

• RANSAC
  随机选取最少需要的点来拟合一个模型
  利用模型验算所有的点，计算出inlier的数量
  重复上述步骤，找出inlier数量最多的模型

• 全景拼接实现
  坑点：ransac必须验证所有的点，在计算H的时候需要搞清楚哪p1和p2之间谁是需要应用H的点集，这里没用用归一化，因为用了归一化之后numpy反而报错.

  def computeH(p1, p2):
      '''
      INPUTS
          p1 and p2 - Each are size (2 x N) matrices of corresponding (x, y)'  
                  coordinates between two images
      OUTPUTS
          H2to1 - a 3 x 3 matrix encoding the homography that best matches the linear 
                  equation
      '''
      assert(p1.shape[0]==p2.shape[0])
      assert(p1.shape[1]==2)
      #############################
      # TO DO ...
      N=p2.shape[0]
      ones=np.ones((N,1))
      main_part=np.concatenate([p2,ones],axis=-1)
      zeros=np.zeros((N,3))
      A=np.concatenate([main_part,zeros,-main_part*p1[:,0:1],zeros,main_part,-main_part*p1[:,1:2]],axis=-1)
      A=A.reshape((2*N,-1))
      A=np.array(A,dtype=float)
      u,s,vh=np.linalg.svd(A,full_matrices=True)
      H2to1=vh[-1].reshape((3,3))
      return H2to1
  
  
  def ransacH(matches, locs1, locs2, num_iter=5000, tol=2):
      '''
      Returns the best homography by computing the best set of matches using RANSAC
      
      INPUTS
          locs1 and locs2 - matrices specifying point locations in each of the images
          matches         - matrix specifying matches between these two sets of point locations
          nIter           - number of iterations to run RANSAC
          tol             - tolerance value for considering a point to be an inlier
  
      OUTPUTS
          bestH - homography matrix with the most inliers found during RANSAC
      '''
  
  
      ###########################
      # TO DO ...
      sample_num = 4
      N=matches.shape[0]
      locs1=locs1[matches[:,0]][:,0:2]
      locs2=locs2[matches[:,1]][:,0:2]
  
      mu_1 = locs1.sum(0) / N
      mu_2 = locs2.sum(0) / N
  
      v_1 = np.sqrt(((locs1 - mu_1) ** 2).sum(1)).mean()
      v_2 = np.sqrt(((locs2 - mu_2) ** 2).sum(1)).mean()
  
      # normal_loc1=(locs1-mu_1)/v_1
      # normal_loc2=(locs2-mu_2)/v_2
      normal_loc1=locs1
      normal_loc2=locs2
  
      sample_space=np.arange(0,N)
  
      bestH=None
      best_inliers=None
      most_inlier=0
      for i in range(num_iter):
          idx=np.random.choice(sample_space,sample_num,replace=False)
          sample_loc1=normal_loc1[idx]
          sample_loc2=normal_loc2[idx]
  
  
          H2to1=computeH(sample_loc1,sample_loc2)
          ones=np.ones((N,1))
  
          x=np.concatenate([normal_loc1,ones],axis=-1)
          u=np.concatenate([normal_loc2,ones],axis=-1)
          Hloc2=H2to1.dot(u.T)# 3xN
          Hloc2=Hloc2.T #Nx3
          Hloc2=Hloc2/Hloc2[:,2:3]
          error=((Hloc2-x)[:,0:2]**2).sum(1)
          n_inlier=(error<=tol).sum()
          if n_inlier>most_inlier:
              bestH=H2to1
              best_inliers=[locs1[idx],locs2[idx]]
              most_inlier=n_inlier
      return bestH,best_inliers
  
  

全景拼接时，首先定义一个output大图，im1按原位放置其中，然后把im2利用cv2.warpPerspective和计算得到的单应性矩阵填入output中。拼接后再两张图交界处有一些痕迹，可以利用这些重叠点和两张图片边界的距离来进行插值。distance_transform_edt函数可以计算图像中一个点，离图像边界(值为0)的最近距离。

相机模型

光圈越大，图像越模糊的原因是物体上多个点映射到像平面上的同一个点。小孔成像中，物体上的每个点只有经过针孔的一条直线到达像平面。 使用凸透镜后物体上一点有多条光线到达相平面，但是聚焦点还是由过中心点的光线决定，所以还是可以使用针孔相机的模型。针孔相机模型中，为了方便，使用一个虚拟像平面。它的内容和像平面相同，但是方向相反。
径向畸变

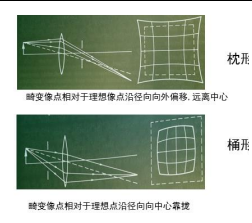
从空间点P到图像点P’的变换不属于线性变换

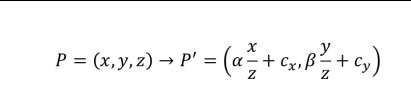
但是可以把P’先转到齐次坐标Ph’，空间点P也转成齐次坐标Ph，然后Ph就可以通过线性变换转到Ph’。一个欧式坐标只能转成一个齐次坐标，即在添加一个值为1的维度，而多个其次坐标可能转成相同的欧式坐标。
从摄像机齐次空间坐标到像素平面齐次坐标的投影矩阵M=K[I,0]，为内参矩阵。内参有五个自由度， $\alpha$和$\beta$是像平面和像素平面的单位换算系数，$\theta$是像平面x,y轴的夹角

规范化投影直接把齐次空间坐标变成齐次平面坐标。

现在需要建立世界坐标系到像素坐标系的映射关系

其中R的每一行由相机坐标系的基向量组成，$R{P}_w$得到是$P_w$在三个基向量上的投影坐标，
T是世界坐标系原点在相机坐标系中的坐标。
同时，在欧式坐标系下，世界坐标$P_{\omega }=R^{\top }(p-T)$,R为正交矩阵。外参有6个自由度。

如果忽略物体的深度，那么可以使用弱透视投影模型，即投影矩阵M的最后一行为[0,0,0,1]

• 相机标定
  给定一系列$p_i$和$P_i$的对应关系，求出矩阵M（3x4）的值
  $p_i=\left[\begin{array}{c}{u}_i\\ v_i\end{array}\right]=\left[\begin{array}{l}\frac{m_1{P}_i}{m_3{P}_i}\\ \frac{m_2{P}_i}{m_3{P}_i}\end{array}\right]M=\left[\begin{array}{c}{m}_1\\ m_2\\ m_3\end{array}\right]$
  其中$P_i$用齐次坐标，一对$p_i$和$P_i$可以得到两个方程，所以只要6对点就可以求出M矩阵（不能在同一个平面上）。并且可以看出M矩阵可以乘以任意系数，并不影响方程的成立。
  可以整理得到超定其次方程组
  
  其中$m$是由M矩阵的3行转置后拼接而成的12维的列向量。然后就是利用奇异值分解求出$m$。
  求出m并重新组合成M=[A,b]矩阵后，可以分别求出内参和外参。
  
  因为$r_3^T$是一个单位向量，所以系数$\rho =\frac{\pm 1}{|a_3|}$. 其它参数的求法如下：
  
  径向畸变模型
  
  由于得到的不是线性方程组，解决方法是先求解出线性部分，即m1,m2然后再用梯度下降法求出m3和$\lambda$.
  
• 影消点影消线
  

平行线的影消点只和它的方向$d$有关，获取影消点的方法是从相机点C画一条方向为$d$的射向，它和像平面的交点就是影消点。 在三维空间中过A点的直线可以用齐次坐标表示为为$\mathbf{X}(\lambda )=\mathbf{A}+\lambda \mathbf{D}$, 经过投影变换后得到$\mathbf{x}(\lambda )=\mathrm{P}\mathbf{X}(\lambda )=\mathrm{P}\mathrm{A}+\lambda \mathrm{P}\mathrm{D}=\mathbf{a}+\lambda \mathrm{K}\mathbf{d}$, 令$\lambda$为无穷大，可得影消点
$\mathbf{v}={\lim }_{\lambda \to \infty }\mathbf{x}(\lambda )={\lim }_{\lambda \to \infty }(\mathbf{a}+\lambda \mathrm{K}\mathrm{d})=\mathrm{K}\mathbf{d}$.

平行面的影消线只和其法向量n有关，获取影消线的方法是过相机点做一个法向量为n的平面。其和像平面的交线就是影消线。在二维空间中，直线可以表示为${\left[\begin{array}{c}{x}_1\\ x_2\\ 1\end{array}\right]}^T\left[\begin{array}{l}a\\ b\\ c\end{array}\right]=0$
过原点并且法向量为$n$的平面在像平面上的投影线$l$可以表示为$K^{-T}n$,因为把$l$上的点x投影回三维空间可以得到$d=K^{-1}x$,这个点和法向量$n$垂直，即${\mathbf{d}}^{\top }\mathbf{n}={\mathbf{x}}^{\top }{\mathrm{K}}^{-\top }\mathbf{n}=0$,因为l同样满足${\mathbf{x}}^{\top }l=0$所以$l=K^{-T}n$

两组平行线之间的夹角可以用影消点坐标和内参表示， 如果已知夹角为90度，就可以通过两个影消点求出相机内参。

• 双视图几何
  
  已知x1即其对应点x2，如何求出X在空间中坐标的问题，其中e1,e2为对极点，C1到C2的连线为为基线，由X,x1,x2组成的平面为极平面，极平面和两个图像平面的交线l1和l2为对极线。
  如果已知x1,需要在另一幅图像中搜索对应点x2,可以用极限约束来简化这个过程，即可以事先求出x2所在的极线l2。
  

假设相机C1的投影矩阵为P1，因为P1不是方阵，所以可以用P1的伪逆$P_1^{+}=P_1^T{\left(P_1{P}_1^T\right)}^{-1}$将x1投影回射线上的某一点$P_1^{+}{x}_1$。 然后可以利用相机C2的投影矩阵P2求出该点在C2相平面的投影点以及e2(C1通过基线投影到e2)的非齐次坐标$P_2{P}_1^{+}{x}_1$和$P_{2}C1$。 已知两点的非齐次坐标，他们之间的连线可以表示成叉乘的形式
$l_2=\left(P_2{C}_1\right)\times \left(P_2{P}_1^{+}{x}_1\right)=e_2\times \left(P_2{P}_1^{+}{x}_1\right)=e_2^{\wedge }\left(P_2{P}_1^{+}{x}_1\right)=\left(e_2^{\wedge }{P}_2{P}_1^{+}\right)x_1$

其中$e_2^{\wedge }{P}_2{P}_1^{+}$为基础矩阵，它乘以x1就得到了过x2的极线。

这里使用了叉乘的矩阵表示:
$a\times b=\left[\begin{array}{ccc}0& -a_z& a_y\\ a_z& 0& -a_x\\ -a_y& a_x& 0\end{array}\right]\left[\begin{array}{l}{b}_x\\ b_y\\ b_z\end{array}\right]=\left[a^{\wedge }\right]b$
叉乘矩阵还有其它性质:
$\hat{b}\times \hat{a}={\hat{b}}^T[\tilde{a}]$ (1)
$[\tilde{a}{]}^T=-[\tilde{a}]$ (2)
注意伪逆是不可能100%还原变换前的坐标，比如不能能通过规范化矩阵$\left[\begin{array}{llll}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]$的伪逆知道变换前第四维的值。
$[\mathbf{x}{]}_{\times }\mathbf{M}={\mathbf{M}}^{-T}{\left[{\mathbf{M}}^{-1}\mathbf{x}\right]}_{\times }$ (3)

假设以C1为世界坐标系则有，
$P_1=K_1[I\mid \tilde{0}],P_2=K_2[R\mid t]$
$P_1^{+}=\left[\begin{array}{c}{K}_1^{-1}\\ {\tilde{0}}^T\end{array}\right],C_1=\left[\begin{array}{l}\tilde{0}\\ 1\end{array}\right],C_2=\left[\begin{array}{c}-R^{T}t\\ 1\end{array}\right]$

其中C2是因为$P_2{C}_2=R{C}_2+t=0$

代入得基础矩阵为${\left[k_{2}t\right]}^{\wedge }{k}_{2}R{k}_1^{-1}$ 而${\left[k_{2}t\right]}^{\wedge }{k}_2$根据性质3可以转换为$k_2^{-T}[t{]}^{\wedge }$,最后得到$k_2^{-T}[t{]}^{\wedge }R{k}_1^{-1}$.

如果两个相机的内参一样，并且令$p_1=K^{-1}{x}_1,p_2=K^{-1}{x}_2，E=R{\left(R^{T}t\right)}^{\wedge }=t^{\wedge }R$ 则有$p_2^{T}E{p}_1=0$，其中E为本质矩阵

本质矩阵有性质：
$Ee=0\text{ 与 }{E}^T{e}^{\prime }=0$
所以E的行列式为0且秩为2，并且有5个自由度 （三个旋转+三个平移，考虑齐次坐标在scale上的等价性去掉一个自由度）E是奇异的，因为t^的秩为2.

从世界坐标系a下的像素点转换到相机坐标系b下的像素点需要的单应性矩阵为
${\mathbf{H}}_{ba}={\mathbf{K}}_b{\mathbf{R}}_{ba}\left(\mathbf{I}+\frac{1}{d_a}\cdot {\mathbf{t}}_{ab}{\mathbf{n}}_a^{\top }\right){\mathbf{K}}_a^{-1}$
其中n和d为像素点对应三维点所在平面再坐标系a下的参数，可以看出如果点在不同的平面上，对应的单应性矩阵也不同。

已知平面上的点和其投影，有下面的关系
$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\lambda \underset{A}{\underbrace{\left[\begin{array}{lll}f\cdot s_x& f\cdot s_{\theta }& u_c\\ 0& f\cdot s_y& v_c\\ 0& 0& 1\end{array}\right]}}\left[\begin{array}{lll}{r}_{11}& r_{12}& t_x\\ r_{21}& r_{22}& t_y\\ r_{31}& r_{32}& t_z\end{array}\right]\left[\begin{array}{l}{x}_w\\ y_w\\ 1\end{array}\right]$
其中中间两个矩阵的乘积可以看成是单应性矩阵$H=[h1,h2,h3]=\lambda \cdot A\cdot \left[r_1,r_2,t\right]$，并且r1和r2是正交并且使单位向量。 这里为什么可以省略r3, 因为r1和r2可以看成是三维点所在平面内的两个坐标轴经过旋转平移变换后的向量，然后t可以看成旋转平移后从原点到平面的向量，这里要求世界坐标系建立在这个平面上。有了上面关系后，如果已知内参A和单应性矩阵H，就可以很轻易的求出r1，r2和t，然后根据r1和r2求出r3。
$h_1=\lambda \cdot A\cdot r_1\Rightarrow r_1=s\cdot A^{-1}\cdot h_1$
$h_2=\lambda \cdot A\cdot r_2\Rightarrow r_2=s\cdot A^{-1}\cdot h_2$
$h_3=\lambda \cdot A\cdot t\Rightarrow t=s\cdot A^{-1}\cdot h_3$

如果给定三维空间中两组点，需要求它们之间的旋转平移矩阵，可以用icp算法。可以转成优化问题
$F(R)={\sum }_{i=1}^N{\Vert R\cdot {\hat{p}}_s^i-{\hat{p}}_t^i\Vert }^2$
又根据$R^{T}R=I$可以得到最佳旋转矩阵为$R^{\ast }=\underset{R}{\mathrm{argmax}}\left({\sum }_{i=1}^N{\hat{p}}_t^{i^T}R{\hat{p}}_s^i\right)$
把它写成迹的形式有
$\begin{array}{rl}\mathrm{trace}\left(P_t^{T}R{P}_s\right)& =\mathrm{trace}\left(R{P}_s{P}_t^T\right)\\ & =\mathrm{trace}(RH)\\ & =\mathrm{trace}\left(RU\Sigma V^T\right)\\ & =\mathrm{trace}\left(\Sigma V^{T}RU\right)\end{array}$
可以看出$V^{T}RU$是正交矩阵，其为单位矩阵的时候上述的迹有最大值。求出R后可以很容易的求出平移向量
$\begin{array}{rl}t& =\frac{1}{N}\sum _{i=1}^N{p}_t^i-R\frac{1}{N}\sum _{i=1}^N{p}_s^i\\ & ={\bar{p}}_t-R{\bar{p}}_s\end{array}$

已知单应性矩阵以及内参，还有一种方法求出旋转矩阵R和平移向量t，并且保证旋转矩阵是正交的。
已知匹配点都在一个平面上所以有
${\mathbf{X}}_2=\left(R+\frac{1}{d}\mathbf{t}{\mathbf{n}}^T\right){\mathbf{X}}_1$
有根据投影模型
${\mathbf{X}}_2=K_2^{-1}H{K}_1{\mathbf{X}}_1$
这里单应性矩阵H可以乘以任意常数
令$A=dR+{\mathbf{t}\mathbf{n}}^T=d{K}_2^{-1}H{K}_1$ (1)
对 $A$ 进行奇异值分解得到 $A=U\Lambda V^T\left(U^{T}U=V^{T}V=I\right),\Lambda =\mathrm{diag}\left(d_1,d_2,d_3\right)$ $\left(d_1\ge d_2\ge d_3\right)$ ，然后把$U^T$和$V$乘到（1）式的两端就得到
$\Lambda =\left[\begin{array}{ccc}{d}_1& 0& 0\\ 0& d_2& 0\\ 0& 0& d_3\end{array}\right]=d^{\prime }{R}^{\prime }+t^{\prime }{\mathbf{n}}^r$
其中
$\{\begin{array}{l}{R}^{\prime }=s{U}^{T}RV\\ {\mathbf{t}}^{\prime }=U^T\mathbf{t}\\ {\mathbf{n}}^{\prime }=V^T\mathbf{n}\\ d^{\prime }=sd\\ s=\det U\det V\end{array}$
这里在R’和d’中包含s项的原因是用来控制d’的符号，因为平面方程$\frac{1}{d}{\mathbf{n}}^T\mathbf{X}=1$中d的符号是任意的。
然后可以得到
$\left(d^{\prime 2}-d_1^2\right)\left(d^2-d_2^2\right)\left(d^{r2}-d_3^2\right)=0$
经过讨论之后，得出d’只能等于d2或-d2, 这两种情况。另外n’向量又有四种情况
$\{\begin{array}{l}{x}_1={\epsilon }_1\sqrt{\frac{d_1^2-d_2^2}{d_1^2-d_3^2}}\\ x_2=0{\epsilon }_1,{\epsilon }_3=\pm 1\\ x_3={\epsilon }_3\sqrt{\frac{d_2^2-d_3^2}{d_1^1-d_3^2}}\end{array}$
但实际上n的符号和d挂钩，所以n’只有两种情况。

根据d’的符号，旋转转换后的旋转矩阵R’和平移向量n’的计算如下：
$\cdot d^{\prime }>0$
$${\mathbf{t}}^{\prime }=\left(d_1-d_3\right)\left(\begin{array}{c}{x}_1\\ 0\\ -x_3\end{array}\right)$$

• $d^{\prime }<0$
  $${\mathbf{t}}^{\prime }=\left(d_1+d_3\right)\left(\begin{array}{c}{x}_1\\ 0\\ x_3\end{array}\right)$$
  可以看出毎种情况，平拜向量都和毎组解有联豕，因此就变成了 $2^{\ast }4=8$ 组解 旋转矩阵的计算公式也是習似：
• $d>0$
  $$\begin{array}{c}{R}^{\prime }=\left(\begin{array}{ccc}\cos \theta & 0& -\sin \theta \\ 0& 1& 0\\ \sin \theta & 0& \cos \theta \end{array}\right)\\ \{\begin{array}{l}\sin \theta =\frac{d_1-d_3}{d_2}{x}_1{x}_3={\epsilon }_1{\epsilon }_3\frac{\sqrt{\left(d_1^2-d_2^2\right)\left(d_2^2-d_3^2\right)}}{\left(d_1-d_3\right)d_2}\\ \cos \theta =\frac{d_1{x}_3^2-d_3{x}_1^2}{d_2}=\frac{d_2^2+d_1{d}_3}{\left(d_1+d_3\right)d_2}\end{array}\end{array}$$
• $d^{\prime }<0$
  $$\begin{array}{c}{R}^{\prime }=\left(\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& -1& 0\\ \sin \theta & 0& -\cos \theta \end{array}\right)\\ \{\begin{array}{l}\sin \theta =\frac{d_1+d_3}{d_2}{x}_1{x}_3={\epsilon }_1{\epsilon }_3\frac{\sqrt{\left(d_1^2-d_2^2\right)\left(d_2^2-d_3^2\right)}}{\left(d_1-d_2\right)d_2}\\ \cos \theta =\frac{d_3{x}_1^2-d_1{x}_3^2}{d_2}=\frac{d_1{d}_3-d_2^2}{\left(d_1-d_3\right)d_2}\end{array}\end{array}$$

基础矩阵F有7个自由度， 因为对于一个nxn矩阵，如果秩为2，那么我们可以证明它的自由度不大于 $n^2-(n-r{)}^2$

F满足$p^{\prime T}Fp=0$
通常情况我们需要的是基础矩阵，使用八点算法来求解

八组点对加上f的模长等于1 的限制得到唯一解，这时我们得到的$\hat{F}$一般是满秩，而F的秩为二，所以再对$\hat{F}$进行SVD分解，保留其最大的两个特征值。
$\mathrm{SVD}(\hat{F})=U\left[\begin{array}{ccc}{s}_1& 0& 0\\ 0& s_2& 0\\ 0& 0& s_3\end{array}\right]V^T\Rightarrow F=U\left[\begin{array}{ccc}{s}_1& 0& 0\\ 0& s_2& 0\\ 0& 0& 0\end{array}\right]V^T$

为了防止各个点的坐标在数值上相差过大，使它们的平均值为0，方差为1。 在实际操作中发现当点集中出现离群点后，均值和方差会被这些离群点支配，所以实践中的做法是直接把坐标值除以图片的宽度来实现归一化。

根据$p^{\prime T}Fp=0$，要想求得图像1(p所在图像)上的极点e1, 那么它必须满足过图像1上的每一条极线，即$p^{\prime T}F{e}_1=0$对任意$p^{\prime }$成立，所以e1应该是F奇异值分解中，特征值为0（最小特征值）对应的特征向量。

奇异值是分解后$\sum$矩阵的对角元素，A矩阵的秩等于奇异值中非零值的个数。假设A为8x9，那么V矩阵的最后一列x一定满足Ax=0，如果限制解的模长为1，那么x为唯一解。

七点法
七个点得到的矩阵A为7x9，所以分解之后V的最后两列组成了A的一个解空间，最后两列分别对应F1和F2，那么最后的F应该为${\mathrm{F}}_1+\lambda {\mathrm{F}}_2$，但是F还必须满足秩为2的约束条件，所以det(F)应该为0，这样就得到了一个3次方程， 可以用待定系数法求出它的多项式形式：

    fun = lambda a: np.linalg.det(a * F1 + (1 - a) * F2)
    a0 = fun(0)
    a1 = 2*(fun(1)-fun(-1))/3-(fun(2)-fun(-2))/12
    a2 = 0.5*fun(1)+0.5*fun(-1)-fun(0)
    a3 = fun(1)-a0-a1-a2

    # solve for the roots of the above polynomial
    roots = np.roots([a3, a2, a1, a0])

然后找出实数解即可

F的误差可以用下式来衡量，$\sum d{\left({\mathrm{x}}_i^{\prime },F{\mathrm{x}}_i\right)}^2+d{\left({\mathrm{x}}_i,{\mathrm{F}}^{\mathrm{T}}{\mathrm{x}}_i^{\prime }\right)}^2$它用投影点和极线的距离来表示误差。 假设直线向量为$l[a,b,c{]}^T$,点的其次向量为x，那么点到直线距离为$l\ast x/sqrt(a^2+b^2)$

三角化
已知，两个视图下匹配点的图像坐标 ${\mathbf{p}}_1$ 和 ${\mathbf{p}}_2$ ，两个相机的相对位姿 $\mathbf{T}$ ，相机内参矩阵 $\mathbf{K}$ ，求对应的三维点坐标 $\mathbf{P}$ ，其齐次坐标为 $\tilde{\mathbf{P}}$
两个视图的投影矩阵分别为
$$\begin{array}{c}{\mathbf{C}}_1=\mathbf{K}\cdot \left[\begin{array}{ll}{\mathbf{I}}_{3\times 3}& 0_{3\times 1}\end{array}\right],{\mathbf{C}}_1\in {\mathbb{R}}^{3\times 4}\\ {\mathbf{C}}_2=\mathbf{K}\cdot \left[\begin{array}{ll}{\mathbf{R}}_{3\times 3}& {\mathbf{t}}_{3\times 1}\end{array}\right],{\mathbf{C}}_2\in {\mathbb{R}}^{3\times 4}\\ \mathbf{T}={\mathbf{T}}_{21}=\left[\begin{array}{ll}\mathbf{R}& \mathbf{t}\end{array}\right]\in {\mathbb{R}}^{3\times 4}\end{array}$$
如果只使用p1，只能求出三维点所在的射线，所以这里用两个方向相等的其次向量叉乘为0的原理建立两个等式
$$\begin{array}{rl}& \widetilde{{\mathbf{p}}_1}\times \left({\mathbf{C}}_1\tilde{\mathbf{P}}\right)=0\\ & \widetilde{{\mathbf{p}}_2}\times \left({\mathbf{C}}_2\tilde{\mathbf{P}}\right)=0\end{array}$$
然后可以得到
${\mathbf{A}}_{4\times 4}\cdot \tilde{\mathbf{P}}=\left[\begin{array}{c}{u}_1{\mathbf{C}}_1^3-{\mathbf{C}}_1^1\\ v_1{\mathbf{C}}_1^3-{\mathbf{C}}_1^2\\ u_2{\mathbf{C}}_2^3-{\mathbf{C}}_2^1\\ v_2{\mathbf{C}}_2^3-{\mathbf{C}}_2^2\end{array}\right]\cdot \tilde{\mathbf{P}}=0$
这里C的上标代表矩阵中的行，下标代表相机。

运动恢复结构

• 欧式结构恢复
  已知n个三维点在m张图像中的坐标，m张图像对应相机的内参数，求出n个三维点的坐标以及m各相机的外参
  求解流程： 用八点法求出基础矩阵，利用内参求出本质矩阵，分解本质矩阵得到旋转平移，最后因为从两张图像上对应点出发的射向不一定相交，用最小化重投影误差的方法找到三维点的坐标
  $X_j^{\ast }=\underset{x_j}{\mathrm{argmin}}\left(d\left(x_{1j},M_1{X}_j\right)+d\left(x_{2j},M_2{X}_j\right)\right)$
  即三角化过程。

为什么叉乘矩阵可以写成$UZ{U}^T$，因为把U写成$[a,b,c]$,把 $Z{U}^T$看成$\left[\begin{array}{c}{b}^{\top }\\ -a^{\top }\\ 0\end{array}\right]$有
$[a,b,c]\left[\begin{array}{c}{b}^{\top }\\ -a^{\top }\\ 0\end{array}\right]=$

$\left[\begin{array}{l}{a}_0{b}_0,a_0{b}_1,a_0{b}_2\\ a_1{b}_0,a_1{b}_1,a_1{b}_2\\ a_2{b}_0,a_2{b}_1,a_2{b}_2\end{array}\right]+\left[\begin{array}{l}-b_0{a}_0,-b_0{a}_1,-b_0{a}_2\\ -b_1{a}_0,-b_1{a}_1,-b_1{a}_2\\ -b_2{a}_0,-b_2{a}_1,-b_2{a}_2\end{array}\right]$$(1)$
可以看出结果和叉乘矩阵一样，对角线为零，并且是反对称矩阵。
假设$T=[x,y,z{]}^T$，从上式可以得到
$\begin{array}{l}x=a_2{b}_1-a_1{b}_2\\ y=a_0{b}_2-a_2{b}_0\\ z=a_1{b}_0-a_0{b}_1\end{array}$
T正好是U矩阵前两列的叉乘，因为U为正交，所以也等于第三列，但是符号可以改变，并且T可以乘以任意系数。

把T的叉乘矩阵分解成上述两种形式的作用就是方便对本质矩阵进行分解，进而得到旋转矩阵以及平移向量。

可以看出将$E=\left[T_x\right]R$中的叉乘矩阵用两种展开方式的其中一种替换之后正好和E进行SVD分解之后的形式对应，从而得到$R=UW{V}^T$ 或者 $U{W}^T{V}^T$，但是R矩阵的行列式应该为正数，所以有$R=\left(\det UW{V}^T\right)UW{V}^T$ 或 $\left(\det U{W}^T{V}^T\right)U{W}^T{V}^T$
又根据前面可以$\mathrm{T}=\pm u_3$ (U的第三列)，所以本质矩阵总共用4种分解方法，

但四种情况中只有三角化交点在两个像平面之前的情况(a)才符合实际.

欧式恢复之后并不知道物体的具体尺寸，但如果我们知道场景中某一条边的长度，那么场景中所有的物体尺寸都能知道。

• 仿射结构恢复

仿射变换M矩阵最后一行为0 0 0 1
所以$x^E={\left(m_{1}X,m_{2}X\right)}^T=\left[\begin{array}{ll}A& b\end{array}\right]X=A{X}^E+b$，这里$x^E$是二维，$X^E$三维

为了消掉b，每张图片上的像素点都减去质心坐标，同时三维点也减去质心坐标
${\hat{x}}_{ij}=x_{ij}-\frac{1}{n}{\sum }_{k=1}^n{x}_{ik}=A_i{X}_j+b_i-\frac{1}{n}{\sum }_{k=1}^n{A}_i{X}_k-\frac{1}{n}{\sum }_{k=1}^n{b}_i$$=A_i\left(X_j-\frac{1}{n}{\sum }_{k=1}^n{X}_k\right)=A_i\left(X_j-\bar{X}\right)=A_i{\hat{X}}_j$
从而把解张图片对应A矩阵的过程转换成一个矩阵分解问题
可以看出D的秩为3，于是保留D奇异值分解中最大的3个特征值（如果没有任何误差的话，其它特征值应该为0）。
这时可以令$U_3$为A1到Am组成的矩阵，并把$U_3$叫做运动M，剩下的叫做结构S. 但是这并不是唯一解，因为可以令M乘以任何可逆的3x3矩阵 ，而S左乘它的逆矩阵。

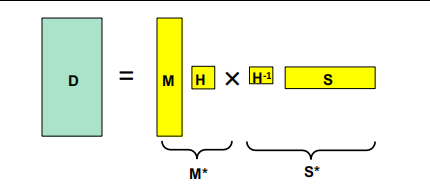
• 透视结构恢复
  先讨论两个视图的情况
  $x_{1\mathrm{j}}=M_1{X}_j$
  $x_{2\mathrm{j}}=M_2{X}_j$
  $j=1\dots ,n$
  和欧式结构恢复的区别在于不知道相机内参，假设相机1的内参为单位矩阵，并且以相机1的坐标系为世界坐标系，根据F矩阵的计算公式${\left[k_{2}t\right]}^{\wedge }{k}_{2}R{k}_1^{-1}$，可以得到$F=\left[b_{\times }\right]A$， $M_2=[A\mid b]$
  然后可以解出b和A。

处理多张图的方法，对每一对图像计算${\tilde{M}}_2$

• bundle adjustment
  先用代数法求出运动和结构的初值，然后同时利用所有图片的重投影误差，进行非线性优化。