元学习中一个很重要的算法MAML,给出了讲解以及对应的代码,现在继续深入这个算法。
四. 基于模型不可知的元学习算法(MAML)
4.2 几种MAML
4.2.1 监督的回归和分类任务
核心和之前是一样的,对于监督学习的话,单输入单输出,我们的损失函数可以定位为:
回归: L ( Φ , D j i ) = ∑ x ( i ) , y ( j ) ∣ ∣ f Φ ( x ( i ) ) − y ( j ) ∣ ∣ 2 2 L(\Phi,{D_j}_i)\ =\ \sum_{x^{(i)},y^{(j)}}||f_{\Phi}(x^{(i)})-y_{(j)}||^2_2 L(Φ,Dji) = ∑x(i),y(j)∣∣fΦ(x(i))−y(j)∣∣22
分类: L ( Φ , D j i ) = ∑ x ( i ) , y ( j ) y ( j ) l o g f Φ ( x ( i ) ) + ( 1 − y ( j ) ) l o g ( 1 − f Φ ( x ( i ) ) ) L(\Phi,{D_j}_i)\ =\ \sum_{x^{(i)},y^{(j)}}y^{(j)}logf_{\Phi}(x^{(i)})\ +\ (1-y^{(j)})log(1-f_{\Phi}(x^{(i)})) L(Φ,Dji) = ∑x(i),y(j)y(j)logfΦ(x(i)) + (1−y(j))log(1−fΦ(x(i)))
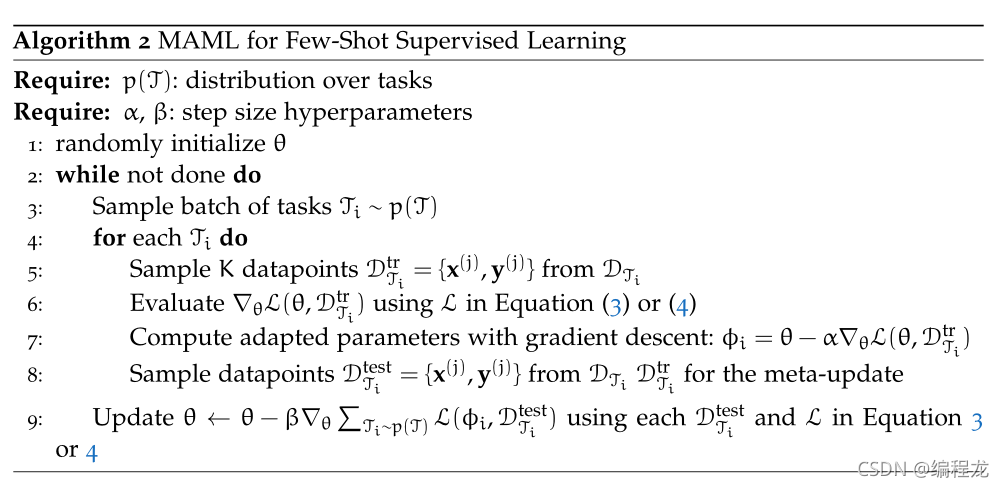
对应着就可以了,实现的代码在上期。
4.2.2 强化学习

强化学习目前还没开始研究所以直接给出代码
4.3 执行和一阶近似
可以发现,之前的MAML算法我们用到了二阶导数,然而二阶导数会增加我们的计算量,因此作者就想用一阶近似去模拟二阶,看是否能代替。优化定义如下:
min θ ∑ J i L ( θ − α s g ( ∇ θ L ( θ , D j t r ) ) , D j i t e s t ) \min _\theta\sum_{J_i}L(\theta\ -\ \alpha\ sg(\nabla_\theta L(\theta,D^{tr}_j)),D^{test}_{j_i}) θminJi∑L(θ − α sg(∇θL(θ,Djtr)),Djitest)
sg表示来停止梯度的操作,这种近似是将参数更新视为一个常数( θ t o θ + c \theta\ to\ \theta+c θ to θ+c),然后反向去传播这个新的性能任务