机器学习基础学习-决策树（信息熵以及基尼系数进行划分）

1、什么是决策树

这里上一个最简单的例子

这样的一个过程形成了一个树的结构，这棵树所有叶子节点的位置就是最终做出的决策，这个决策可以看成对应聘者的信息的输入进行分类（录用或者考察）的过程。这样的一个过程就是决策树。对于决策树来说，他有树结构相应所有的性质（包括节点、深度等）

这里的决策树的深度就是3，因为最多通过3次判断就能将数据进行相应的分类。

这里每一个节点进行决策的属性都可以通过是或者否来回答问题，实际上真实的数据的内容都是具体的数值。

2、通过sklearn了解决策树

（1）生成样本

# 决策树

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 这里先用鸢尾花数据集（150行4列：150个样本，4个特征值）
iris = datasets.load_iris()

X = iris.data[:, 2:] # 只取两个维度的数据特征（方便可视化，保留后两个特征）
y = iris.target

# X[y == 0, 1]：获取y==0的行，然后获取这些行的第二个元素
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == 2, 0], X[y == 2, 1])
plt.show()

（2）调用sklearn的决策树
这里用到sklearn.tree模块的DecisionTreeClassifier
创建决策树

from sklearn.tree import DecisionTreeClassifier
'''
  创建决策树
  max_depth: 决策树最高深度
  entropy: 熵
'''
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
dt_clf.fit(X, y)

（4）调用之前说到过的绘制决策边界的方法

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

调用决策边界

  # 绘制决策边界
  plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3]) # x、y轴的范围
  # 样本
  plt.scatter(X[y == 0, 0], X[y == 0, 1])
  plt.scatter(X[y == 1, 0], X[y == 1, 1])
  plt.scatter(X[y == 2, 0], X[y == 2, 1])
  plt.show()

通过图像分析决策树大概是什么样的决策树，这里所有的特征都是数数值（这里2.4是根据图像估计的）。横轴记为x，纵轴记为y。
A类是蓝色点，B类是橘色的点，C类是绿色的点

这种情况主要是针对决策树面对属性是数值特征时的处理方法：在每一个节点上选择某一个维度和这个维度相应的阈值，根据他们的关系进行选择分支

3、决策树的特征

1、非参数学习算法
2、可以解决分类问题
3、天然可以解决多分类问题（如上一个样本）
4、也可以解决回归问题
5、具有非常好的可解释性（如根据数据进行评级）

4、信息熵概念

构建决策树时，有些问题，针对上一个例子，我们只有两个维度（x,y），可以根据这两个维度对数据进行划分，但是数据复杂起来之后可能有很多个维度，具体在哪个维度上进行划分，进一步在这个维度的上的哪一个阈值进行划分都是我们要考虑的问题。

针对这个问题就要引入信息熵的概念了。
熵
熵的概念主要是信息论里的概念，熵在信息论中代表随机变量不确定度的度量。
熵越大，数据的不确定性越高
熵越小，数据的不确定性越低
（熵的概念最开始引用的是物理热力学里的内容，可以理解成，熵越大相当于热力学中粒子的无规则运动越剧烈，也就是不确定性越高；反之，熵越小，粒子越相对于静止的状态，越倾向于确定的状态，也就是不确定性越低）

信息熵

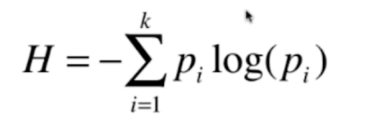
pi：对于系统中k类信息，每一类信息所占的比例（比如鸢尾花数据集共3类，每种占比1/3，所以p1=p2=p3=1/3）

熵代表不确定度的度量，熵越小不确定性越低，对比上面两组数据，第二组数据比第一组数据的确定性越高（有一类数据占总数据的7/10，占比很高，总体数据更加偏向于确定性）

再看一种极端情况

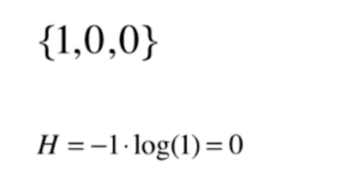
这个时候的信息熵达到了最低值，此时数据的不确定性是最低的，也就是最确定的（所有数据都在一类中，没有任何不确定性）

下面摆出更多信息论的相关公式

5、绘制信息熵函数图像

如果我们的数据类别只有两类，一类占比x，另一类则占比1-x，那么信息熵可以表示成

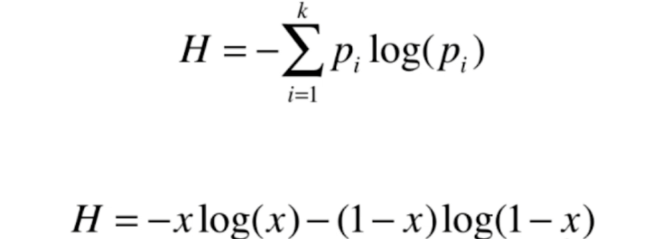
# 绘制信息熵（针对二分类问题）

import numpy as np
import matplotlib.pyplot as plt

'''
  计算信息熵
'''
def entropy(p):
  # 这里的p不仅可以是数字，也可以是向量或者是数组
  return -p * np.log(p) - (1-p) * np.log(1-p)


# x是向量，(0,1)均匀取200个值，不取特殊情况的0、1
x = np.linspace(0.01, 0.99, 200)
plt.plot(x, entropy(x))
plt.show()

可以看到这个曲线类似于一个抛物线，当x=0.5左右时，这个曲线取到了最大值，相当于对于信息熵来说，如果数据只有两个类别的时候，一个类别的占比是0.5，另一个类别占比1-0.5也是0.5的时候，信息熵的值达到最大，此时处于最不确定的状态。
当基于0.5左右，x更大，或者x更小，我们的信息熵的值都会减小，因为无论x增大或者减小，我们数据的值都会更偏向于具体的某一类，整体的确定性变高了，信息熵就变低了。
ps：当系统的每一类数据都是等概的时候，信息熵是最高的

6、根据信息熵划分节点数据

在了解信息熵之后，针对之前的问题就有了解答

划分的依据就是要数据划分之后，系统的总体信息熵降低（让系统更加确定）

对于根节点而言，相当于根节点拥有我们全部的数据，然后我们需要找到一个维度、阈值对根节点进行划分，划分之后我们希望整体信息熵降低，然后对于划分出来的两个节点，我们可以再次用同样的方式去寻找特定的维度和阈值，使总体的信息熵再降低，通过这样方法不断递归，就形成了最终的决策树。

下面模拟根据信息熵进行划分的方式
首先复制第一块：什么是决策树部分的代码，绘制出根据决策树进行分类的决策边界和样本点

# 使用信息熵寻找最优划分

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier

# 这里先用鸢尾花数据集（150行4列：150个样本，4个特征值）
iris = datasets.load_iris()

X = iris.data[:, 2:] # 只取两个维度的数据特征（方便可视化，保留后两个特征）
y = iris.target

'''
  创建决策树
  max_depth: 决策树最高深度
  entropy: 熵
'''
# 训练决策树分类器
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
dt_clf.fit(X, y)

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

# 绘制决策边界
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3]) # x、y轴的范围
# 样本
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == 2, 0], X[y == 2, 1])
plt.show()

接下来模拟使用信息熵进行划分，对比使用sklearn中决策树的划分结果，看划分是否是一致的
定义划分方法

'''
  模拟使用信息熵进行划分
  d:划分维度
  value：阈值
''' 
def split(X, y ,d, value):
  index_a = (X[:, d] <= value) # 定义索引
  index_b = (X[:, d] >value)
  return X[index_a], X[index_b], y[index_a], y[index_b]

求信息熵

from collections import Counter
from math import log
'''
  求信息熵
'''
def entropy(y):
  # 将y值做成字典
  # counter包含键值对，y的取值-y的取值对应的分类个数
  counter = Counter(y)
  res = 0.0
  # 遍历看每一个不同的类别，有多少个样本点
  for num in counter.values():
    p = num / len(y)
    res += -p * log(p)
  return res

划分使信息熵最低

'''
  划分使信息熵最低
  在d列对应特征值的数据寻找信息熵和最小的划分方式
'''
def try_spilt(X, y):
  best_entropy = float('inf')
  best_d, best_v = -1, -1 # 维度、阈值
  # 穷搜
  for d in range(X.shape[1]): # 有多少列（特征），shape[0]有多少行，shape[1]有多少列
    sorted_index = np.argsort(X[:, d]) # 返回第d列数据排序后相应的索引
    for i in range(1, len(X)): # 对每一个样本进行遍历
      if (X[sorted_index[i-1], d] != X[sorted_index[i], d]):
        # d这个维度上从1开始，找i-1 和i的中间值
        # 可选值是在d这个维度上的中间值
        v = (X[sorted_index[i-1], d] + X[sorted_index[i], d]) / 2
        # X_l左子树，X_r右子树
        # 进行划分
        X_l, X_r, y_l, y_r = split(X, y ,d, v)
        #  信息熵的和
        e = entropy(y_l) + entropy(y_r)
        # best_entropy:之前搜索过的某一个信息熵
        if e < best_entropy: # 找到更好的划分方式
          best_entropy, best_d, best_v = e, d, v
  return best_entropy, best_d, best_v

调用try_spilt

best_entropy, best_d, best_v = try_spilt(X, y)
print('best_entropy=', best_entropy)
print('best_d=', best_d)
print('best_v=', best_v)

所以对于这个结果，我们对原始数据的最佳划分是在第0个维度，阈值是2.45的位置进行划分，划分后，信息熵是0.693左右。
这个时候对应最开始调用sklearn决策树进行划分的方式

第一次划分，对应横轴上（第0个维度上）在2.45左右的位置进行了划分。
接下来对于划分后的数据进行存储

# 第一次划分得到的数据
X1_l, X1_r, y1_l, y1_r = split(X, y ,best_d, best_v)
print(entropy(y1_l), 'y1_l的信息熵')

第一次划分后的y2_l 的信息熵为0，因为第一次划分成功的把一类当中的所有数据都划分到了最左边，所以此时这部分的信息熵为0，没有任何的不确定性。所以他的左边已经不需要划分了。
同理可以看y1_r的信息熵

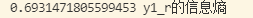
对于右边的一部分信息熵为0.69左右，也就是说还可以继续进行划分

# y1_l对应划分之后左边的部分，信息熵为0，不需要再进行划分
# y1_r对应划分之后右边的部分，信息熵大于0，可以继续进行划分
best_entropy2, best_d2, best_v2 = try_spilt(X1_r, y1_r)
print('best_entropy2=', best_entropy2)
print('best_d2=', best_d2)
print('best_v2=', best_v2)

这个结果对应，第二次划分在第1个维度上（y轴上），1.75的阈值上进行划分，可以使信息熵最低为0.41左右

# 第二次划分得到的数据
X2_l, X2_r, y2_l, y2_r = split(X1_r, y1_r ,best_d2, best_v2)
print(entropy(y2_l), 'y2_l的信息熵')
print(entropy(y2_r), 'y2_r的信息熵')

得到第二次划分的结果

第二次划分，划分出来的两颗子树上的信息熵都没有降为0，所以其实还可以继续划分（这里就不继续模拟了）。在sklearn中的决策树进行划分传的max_depth也是2

7、基尼系数

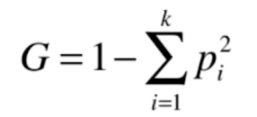
基于基尼系数来说，第二组数据的值比第一组数据的值要小，通过之前信息熵的概念，我们知道第二组的数据不确定性要低一些，这个趋势和信息熵的结果一致，也就是说对于基尼系数而言，数值越低，不确定性也就越低，即越稳定。

在极端的情况下

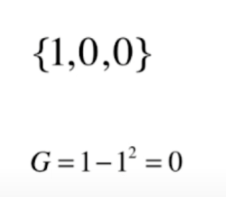
此时基尼系数达到了最低值，基尼系数取0 的时候也就说明所有数据分类在一个类别中，确定性是100%。

8、分析基尼系数函数

化简后的曲线即是一个抛物线，开口向下。即在二分类的情况下，一类占比50%，另一类占比50%的时候，基尼系数最大，不确定性最高。
当x从0.5逐渐增大或者减小的时候，基尼系数逐渐减小，稳定性逐渐提高，直至x为0或者x为1

9、模拟使用基尼系数进行划分

# 模拟使用基尼系数对决策树进行划分

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier

# 这里先用鸢尾花数据集（150行4列：150个样本，4个特征值）
iris = datasets.load_iris()

X = iris.data[:, 2:] # 只取两个维度的数据特征（方便可视化，保留后两个特征）
y = iris.target

'''
  创建决策树
  max_depth: 决策树最高深度
  criterion：划分数据的标准（比如信息熵、基尼系数）
  gini: 基尼系数
'''
# 训练决策树分类器
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="gini")
dt_clf.fit(X, y)

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

# 绘制决策边界
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3]) # x、y轴的范围
# 样本
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == 2, 0], X[y == 2, 1])
plt.show()

这里与通过信息熵进行划分的主要区别在于划分的标准不同，这里的gini表示通过基尼系数进行划分，之前的entropy表示用信息熵进行划分

# 训练决策树分类器
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="gini")

可以看到，在这里通过基尼系数划分的结果和信息熵划分的结果是相同的（其实大部分情况下他们的划分结果都是相同的）。
下面是定义的一些方法
以下的函数部分代码和使用信息熵进行划分的方法大部分都是一样的
区别仅仅在于之前用于计算信息熵的方法，在这里改成了计算基尼系数

'''
  以下的函数部分代码和使用信息熵进行划分的方法大部分都是一样的
  区别仅仅在于之前用于计算信息熵的方法，在这里改成了计算基尼系数
'''

'''
  模拟使用基尼系数进行划分
  d:划分维度
  value：阈值
''' 
def split(X, y ,d, value):
  index_a = (X[:, d] <= value) # 定义索引
  index_b = (X[:, d] >value)
  return X[index_a], X[index_b], y[index_a], y[index_b]


'''
  求基尼系数
'''
def gini(y):
  # 将y值做成字典
  # counter包含键值对，y的取值-y的取值对应的分类个数
  counter = Counter(y)
  res = 1.0
  # 遍历看每一个不同的类别，有多少个样本点
  for num in counter.values():
    p = num / len(y)
    res -= p**2
  return res

'''
  划分使基尼系数最低
  在d列对应特征值的数据寻找基尼系数和最小的划分方式
'''
def try_spilt(X, y):
  best_g = float('inf')
  best_d, best_v = -1, -1 # 维度、阈值
  # 穷搜
  for d in range(X.shape[1]): # 有多少列（特征），shape[0]有多少行，shape[1]有多少列
    sorted_index = np.argsort(X[:, d]) # 返回第d列数据排序后相应的索引
    for i in range(1, len(X)): # 对每一个样本进行遍历
      if (X[sorted_index[i-1], d] != X[sorted_index[i], d]):
        # d这个维度上从1开始，找i-1 和i的中间值
        # 可选值是在d这个维度上的中间值
        v = (X[sorted_index[i-1], d] + X[sorted_index[i], d]) / 2
        # X_l左子树，X_r右子树
        # 进行划分
        X_l, X_r, y_l, y_r = split(X, y ,d, v)
        #  基尼系数的和
        g = gini(y_l) + gini(y_r)
        # best_g:之前搜索过的某一个基尼系数
        if g < best_g: # 找到更好的划分方式
          best_g, best_d, best_v = g, d, v
  return best_g, best_d, best_v

接下来可以进行模拟了

best_g, best_d, best_v = try_spilt(X, y)
print('best_g=', best_g)
print('best_d=', best_d)
print('best_v=', best_v)

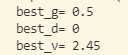
对比sklearn中使用决策树进行划分的结果
第一次划分发生在x轴取值为2.45的时候，划分维度是0（x轴）

# 第一次划分得到的数据
X1_l, X1_r, y1_l, y1_r = split(X, y ,best_d, best_v)
print(gini(y1_l), 'y1_l的基尼系数')
print(gini(y1_r), 'y1_r的基尼系数')

y1_l的基尼系数为0，因为左边这些蓝色的点都被完全划分出去了，不确定性达到最小。
y1_r的基尼系数不为0 ，那么可以继续进行划分

# y1_l对应划分之后左边的部分，基尼系数为0，不需要再进行划分
# y1_r对应划分之后右边的部分，基尼系数大于0，可以继续进行划分
best_g2, best_d2, best_v2 = try_spilt(X1_r, y1_r)
print('best_g2=', best_g2)
print('best_d2=', best_d2)
print('best_v2=', best_v2)
# 第二次划分得到的数据
X2_l, X2_r, y2_l, y2_r = split(X1_r, y1_r ,best_d2, best_v2)
print(gini(y2_l), 'y2_l的基尼系数')
print(gini(y2_r), 'y2_r的基尼系数')

经过搜索查询，第二次划分将在维度为1（y轴），阈值为1.75的位置进行划分，对比之前调用sklearn决策树的划分结果，分类结果也是一致的，此时的基尼系数降低到了0.21左右，和之前的0.5相比，也是将低了的

10、信息熵vs基尼系数

（1）熵信息的计算比基尼系数稍慢。
信息熵的计算涵盖了log的计算；基尼系数主要计算平方，然后用1减去

（2）scikit-learn中默认为基尼系数
这里如果调用sklearn决策树的划分，默认划分方式是gini系数的划分方式

（3）大多数时候二者没有特别的效果优劣