神经网络学习笔记6——一些其他选择

这是我参与11月更文挑战的第11天

随机梯度下降的改进

Hessian技术

Hessian 技术是一种最⼩化代价函数的⽅法，对于 $C=C(w),w=w_1,w_2,...$。通过泰勒展开式（如果函数满足一定的条件，泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数），代价函数可以在点 $w$处被近似为：

$$C(w+\Delta w)=C(w)+\sum_j\frac{\partial C}{\partial w_j}\Delta w_j+\frac{1}{2}\sum_{jk}\Delta w_j\frac{\partial^2 C}{\partial w_j\partial w_k}\Delta w_k+...$$

可以将其简化为：

$$C(w+\Delta w)=C(w)+\nabla C\Delta w+\frac{1}{2}\Delta w^TH\Delta w+...$$

$\nabla C$表示梯度向量， $H$为Hessian矩阵，矩阵中的第 $jk$项为 $\frac{\partial^2 C}{\partial w_j\partial w_k}$。

为简化计算更高阶的项可以省略得到近似的 $C$值：

$$C(w+\Delta w) \approx C(w)+\nabla C\Delta w+\frac{1}{2}\Delta w^TH\Delta w$$

证明右式表达式可以进⾏最⼩化（即函数图形是凹的），方法：求 $C(w+\Delta w)''，并证明C(w+\Delta w)''> 0$，Hessian矩阵有一个性质在其为正定矩阵时函数的二阶偏导数恒>0，Hessian矩阵和函数凹凸。令：

$$\Delta w=-H^{-1}\nabla C$$

则： $w+\Delta w = w-H^{-1}\nabla C$

在实际应用中， $\Delta w = -\eta H^{-1}\nabla C$，其中 $\eta$为学习是速率。Hessian ⽅法⽐标准的梯度下降⽅法收敛速度更快，而且通过引⼊代价函数的⼆阶变化信息，可以让 Hessian ⽅法避免在梯度下降中常碰到的多路径（pathologies）问题。

然而 Hessian ⽅法中Hessian 矩阵计算非常麻烦，对于拥有 $10^7$个权重的网络，对应的Hessian矩阵会有 $10^7\times 10^7$个元素，计算量非常大。

基于 momentum 的梯度下降

基于 momentum 的梯度下降对Hessian ⽅法做了改进，避免产生太大矩阵问题（即避免产生二阶导数的矩阵），是一种优化方法。 momentum方法引入了物理中速度的概念引入了速度（velocity）的参数 $v$和表示摩擦力的项 $\mu$（moment coefficient）， $C$的表示方法变为：

$$v\rightarrow v'=\mu v-\eta \nabla C \\ \ \\ w\rightarrow w'=w+v'$$

为理解这个公式，先考虑 $\mu=1$（即没有摩擦力）时会发生什么， $v=v-\eta\nabla C, w=w+v-\eta\nabla C$，对于下图可以看到每⼀步速度都不断增⼤，所以会越来越快地达到⾕底，从而确保 momentum 技术⽐标准的梯度下降运⾏得更快。

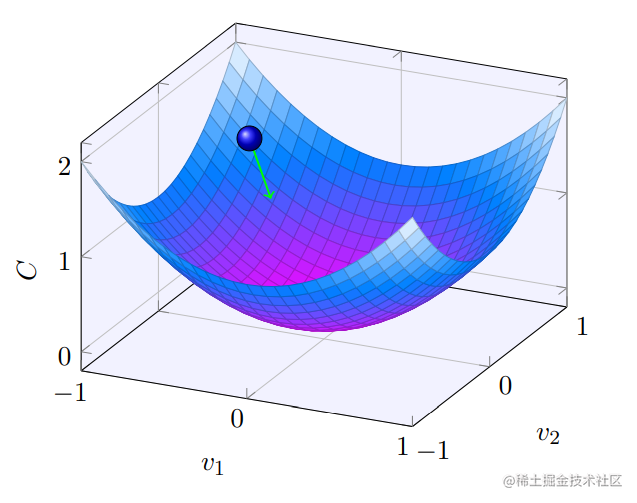
但之前提到过过大的下降步长（或速度）会导致下降接近底部时越过谷底发生震荡影响学习速度，为解决这个问题引入了摩擦力 $\mu$这个参数来控制下降速度，当 $\mu = 1$时没有摩擦力，速度完全由梯度 $\nabla C$的大小决定。 $\mu =0$时，速度就没有作用，回到原来的梯度下降方法。实践中一般通过 hold out验证数据集来选择合适的 $\mu$，和之前选择 $\eta$的方法类似。

人工神经元的其他模型

之前提到的神经元都是S型神经元，理论上说S型神经元可以拟合任何分布。但是在实践中对于某些应用其他神经元的学习效果可能更好。

tanh神经元

使用双曲正切函数（hyperbolic tangent）替代S型函数：

$$tanh(wx+b) \\ \ \\ tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}},\ z=wx+b$$

回忆Sigmiod函数的公式 $\sigma(z)$：

$$\sigma(z)=\frac{1}{1+e^{-z}}$$

练习： 证明 $\sigma(z)=\frac{1+tanh(z/2)}{2}$

$$tanh(z/2)=\frac{e^{z/2}-e^{-z/2}}{e^{z/2}+e^{-z/2}}=\frac{e^{z/2}-e^{-z/2}}{e^{z/2}+e^{-z/2}}\frac{e^{z/2}-e^{-z/2}}{e^{z/2}-e^{-z/2}}= \frac{e^2-2e^0+e^{-z}}{e^z-e^{-z}} \\ \ \\ tanh(z/2)+1=\frac{e^z-2+e^{-z}}{e^z-e^{-z}}+\frac{e^z-e^{-z}}{e^z-e^{-z}}=\frac{2(e^z-1)}{e^z-e^{-z}}=\frac{2(e^z-1)}{(e^z-1)(1+e^{-z})}=2\sigma(z)$$

综上可知，tanh函数实际上是Sigmoid函数按比例变化后形成的，其形状也其相似，如下所示：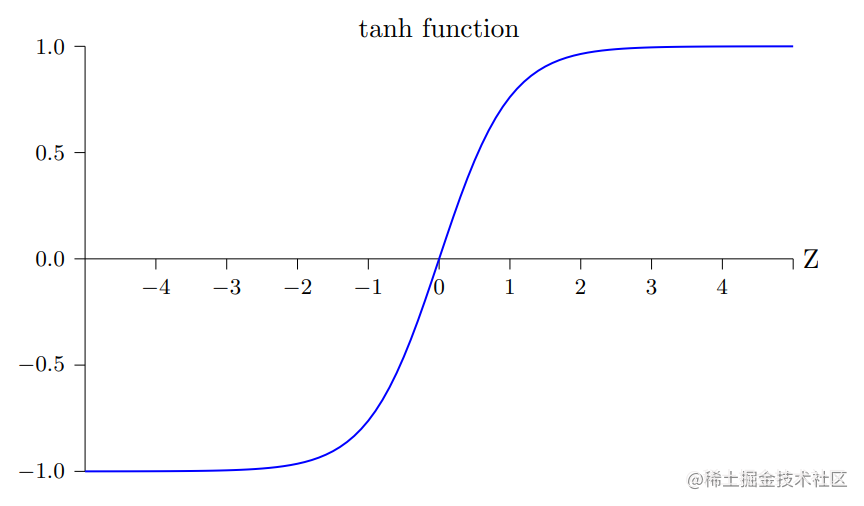

两个函数之间的差异就是 tanh 神经元的输出的值域是 (−1, 1) ⽽⾮ (0, 1)，因此在使用tanh神经元时可能需要正则化最终的输出将激活值限制到0-1之间。

tanh和S型神经元使用上的差异

使⽤ S 型神经元，所有激活值都是正数，反向传播中梯度为 $a\delta$，激活值必然为正数，则梯度的正负只和 $\delta$有关，针对同⼀神经元的所有权重都会或者⼀起增加或者⼀起减少，在某些情况下同⼀神经元的权重可能需要有相反的变化，⽤tanh神经元可能是更好的选择。这只是一种启发式的想法，目前的研究没有快速准确的规则说哪种类型的神经元对某种特定的应⽤学习得更快，或者泛化能⼒最强。

ReLU神经元

ReLU神经元，即修正线性神经元（rectified linear neuron）或者修正线性单元（rectified linear unit），其输出为：

$$max(0,wx+b)$$

图像如下所示：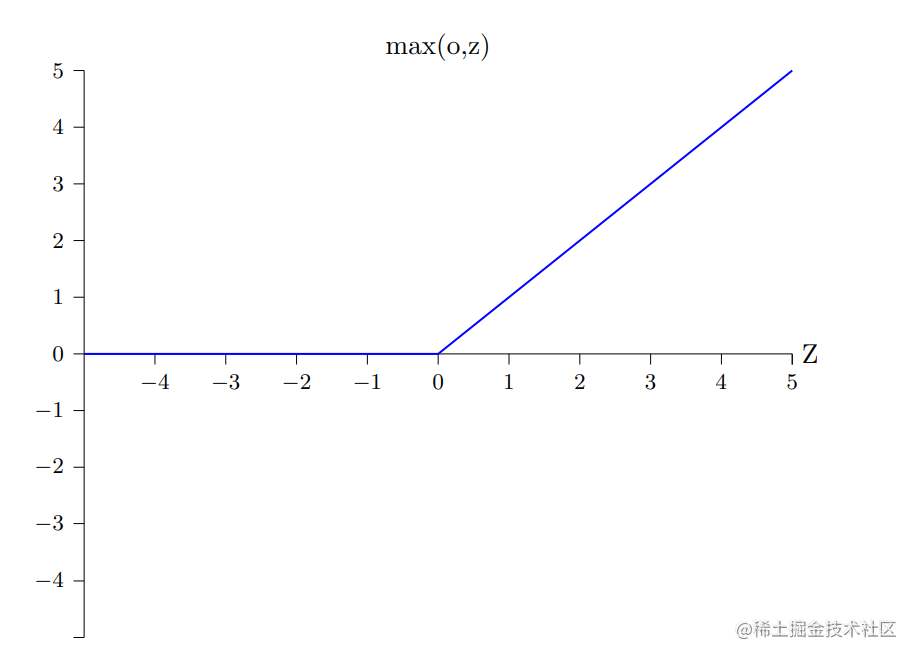

在一些图像识别工作中ReLU神经元展现了很好的效果。