[集训队作业2018] count（笛卡尔树，生成函数，卡特兰数）

传送门

什么情况下两序列同构

对于两序列$A[1,n],B[1,n]$，设$f_A(1,n)=p_a,f_B(1,n)=p_b$，

• 若$p_a\ne p_b$，$A,B$一定不同构。
• 若$p_a=p_b$，
  若$A[1,p_a-1]$与$B[1,p_b-1]$同构且$A[p_a+1,n]$与$B[p_b+1,n]$同构，则$A[1,n],B[1,n]$同构；
  否则$A,B$不同构。

由这个过程想到什么？笛卡尔树！
没错，两序列同构当且仅当它们的笛卡尔树形态相同。

生成函数做法

引理证明：
A = { X ∣ 序 列 X 长 度 为 n , 序 列 X 中 的 每 个 数 都 是 1 到 m 内 的 整 数 } A=\{X| 序列X长度为n,序列X中的每个数都是1到m内的整数\} A={ X∣序列X长度为n,序列X中的每个数都是1到m内的整数}
B = { X ∣ 序 列 X 长 度 为 n , 序 列 X 中 的 每 个 数 都 是 1 到 m 内 的 整 数 ， 且 序 列 X 中 的 最 大 值 为 m } B=\{X| 序列X长度为n,序列X中的每个数都是1到m内的整数，且序列X中的最大值为m\} B={ X∣序列X长度为n,序列X中的每个数都是1到m内的整数，且序列X中的最大值为m}
C = { X ∣ 序 列 X 长 度 为 n , 序 列 X 中 的 每 个 数 都 是 1 到 m 内 的 整 数 ， 且 所 有 1 到 m 内 的 整 数 都 在 序 列 X 中 出 现 过 } C=\{X| 序列X长度为n,序列X中的每个数都是1到m内的整数，且所有1到m内的整数都在序列 X 中出现过\} C={ X∣序列X长度为n,序列X中的每个数都是1到m内的整数，且所有1到m内的整数都在序列X中出现过}
可以证明$n\ge m$时，$A=B=C$。

证明：
首先证明$A=B$。
对于$A$中任意一个序列$X$，若$X$中的最大值为$p$，那么把$X$中的每个数都加上$m-p$，得到序列$Y$ ，显然$X$和$Y$同构，即$X=Y$ 。$Y$中最大值为$m$，即$Y\in B$。
对于任意 $X\in A$，均有$X\in B$，这说明$A\subseteq B$。而 $B\subseteq A$ 是显然的，因此 $A=B$。

可以利用类似的方法证明 $A=C$。
对于$A$中任意一个序列$X$，可以在同构的前提下，保持不同权值的数之间的相对大小的同时，把权值相同的数按下标顺序替换成权值不同的数。这样在$n\ge m$时，通过上述替换，可以使$X$中出现过的数增加至$m$种。
对于任意$X\in A$，均有$X\in C$，这说明$A\subseteq C$。$C\subseteq A$ 也是显然的，因此 $A=C$。

DP：
设$f[i][j]$表示$n=i,m=j$时的$|C|$，那么$f[i][j]=|C|=|A|=|B|$。
考虑计算$|B|$，那么最大值为$j$，枚举下标最小的$j$的下标，得到递推式：
$$f[i][j]=\sum _{p=1}^{i}f[p-1][j-1]\times f[i-p][j]$$
(把$f[p-1][j-1]$当$|A_1|$，$f[i-p][j]$当$|A_2|$)

引入生成函数：
设$F_j(x)={\sum }_{i\ge 0}f[i][j]x^i$，代入递推式有：
$$F_j(x)[x^i]=\sum _{p=1}^i{F}_{j-1}(x)[x^{p-1}]\times F_j(x)[x^{i-p}]$$
$$F_j(x)[x^i]=\sum _{p=0}^{i-1}{F}_{j-1}(x)[x^p]\times F_j(x)[x^{i-1-p}]$$
$$F_j(x)[x^i]=(F_{j-1}(x)\times F_j(x))[x^{i-1}]$$
平凡情况有$f[0][j]=1$。

所以$F_j(x)=F_j(x)F_{j-1}(x)x+1$
所以$F_j(x)=\frac{1}{1-F_{j-1}(x)x}$

直接做似乎很不可做，但由这个式子我们知道$F_j$可以分解为$\frac{A_j}{B_j}$，其中$A_j,B_j$是两个次数界为$O(j)$的多项式，那么考虑求$A_j,B_j$：

$$\frac{A_j}{B_j}=\frac{1}{1-\frac{A_{j-1}}{B_{j-1}}x}$$
$$\frac{A_j}{B_j}=\frac{B_{j-1}}{B_{j-1}-A_{j-1}x}$$

扫描二维码关注公众号，回复： 13247858 查看本文章

于是得到$A_j=B_{j-1},B_j=B_{j-1}-A_{j-1}x$，将转移关系用矩阵来表示就得到：

$$\left[\begin{array}{cc}0& 1\\ -x& 1\end{array}\right]\left(\begin{array}{c}{A}_{j-1}\\ B_{j-1}\end{array}\right)=\left(\begin{array}{c}{A}_j\\ B_j\end{array}\right)$$

那么可以通过矩阵快速幂来求$A_j,B_j$。但是直接在矩阵中用多项式进行计算会很麻烦，因此不妨考虑用单位根代入求点值，用$IDFT$插出多项式即可。复杂度$O(nlogn)$。

参考博客

卡特兰数做法

因为两序列同构当且仅当它们的笛卡尔树形态相同，所以原题就是问有多少棵不同形态的节点数为$n$的笛卡尔树满足要求。

为了满足题目中所给出的 “如果有多个最大值，取下标最小的” 的要求，规定笛卡尔树上的节点$x$满足：左儿子的值$<x$的值&&右儿子的值$\le x$的值

根据上文引理的证明，
“序列中的每个数都是1到$m$内的整数，且所有$1$到$m$内的整数都在序列中出现过”的条件
等价于 “序列中的每个数都是1到$m$内的整数”，
所以一棵笛卡尔树有符合条件的填数方法，当且仅当 从根节点往下走，不存在一种走法，使得往左儿子走的次数$>m-1$（每往左儿子走一次，相当于权值 −1，需要有数可填）

考虑将"往左儿子走的次数$\le m-1$"的条件进行转换，变为更容易处理的问题：
想到多叉树转二叉树的方法：节点$x$的左儿子为原树上$x$的儿子，右儿子为原树上$x$的兄弟
考虑把笛卡尔树这棵二叉树转回多叉树（存在转换后构不成一棵树的情况，需要新增一个虚点作为根节点），
“笛卡尔树上往左儿子走的次数$\le m-1$” 等价于 “记虚点的深度为0，多叉树的深度要$\le m$”。
问题变成统计 有$n+1$个节点，深度$\le m$的不同形态的多叉树棵树

考虑树的括号表示，再稍微改一下定义

以这棵树为例，常规的括号表示法为1(2(4(8,9),5(10,11)),3(6(12),7))，我把它改成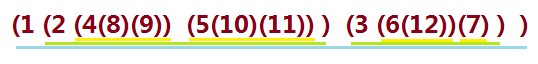
从左到右遍历多叉树对应的括号序列（不算最外层根代表的那对括号），要求任何时候 $左括号数量\ge 右括号数量$（括号序列性质），$左括号数量-右括号数量\le m$（树的深度$\le m$）

把统计合法的括号序列个数 转化为 统计折线数量：
从左到右遍历括号序列，每遍历到一个括号，$x$坐标+1，如果遍历到的是左括号则$y$坐标+1，遍历到的是右括号则$y$坐标-1。起点为$(0,0)$，终点为$(2n,0)$。由于对括号序列的限制，行走过程中不能经过$y=-1$，$y=m+1$这两条直线。

原问题转为 统计从$(0,0)$走到$(2n,0)$，每次$x+1$，$y+1或-1$，不经过$y=-1$，$y=m+1$这两条直线的合法方案数。

先简化问题：只限制折线不能经过$y=-1$，不限制其不能经过$y=m+1$

记$A_{(x1,y1)\to (x2,y2)}$为从$(x1,y1)$走到$(x2,y2)$，不考虑是否经过某些直线的方案数，
$B_{(x1,y1)\to (x2,y2)}$为从$(x1,y1)$走到$(x2,y2)$，经过$y=-1$的方案数，
$C_{(x1,y1)\to (x2,-1)}$为从$(x1,y1)$走到$(x2,-1)$，在$(x2,-1)$第一次经过$y=-1$的方案数。

$A_{(x1,y1)\to (x2,y2)}=C_{x2-x1}^{\frac{x2-x1+y2-y1}{2}}$（相当于在$x2-x1$步中选$\frac{x2-x1+y2-y1}{2}$步令$y$坐标+1）

考虑容斥，简化版问题的答案为$A_{(0,0)\to (2n,0)}-B_{(0,0)\to (2n,0)}$
$$B_{(0,0)\to (2n,0)}=\sum _{p=1}^{2n-1}{C}_{(0,0)\to (p,-1)}\times A_{(p,-1)\to (2n,0)}$$
设$s^{\prime }$与$s(0,0)$关于$y=-1$对称，根据对称性$C_{(0,0)\to (p,-1)}=C_{s^{\prime }\to (p,-1)}$
所以
$$B_{(0,0)\to (2n,0)}=\sum _{p=1}^{2n-1}{C}_{s^{\prime }\to (p,-1)}\times A_{(p,-1)\to (2n,0)}$$
等式右侧那坨式子的组合意义就是$A_{s^{\prime }\to (2n,0)}$
所以
$$B_{(0,0)\to (2n,0)}=A_{s^{\prime }\to (2n,0)}$$

再考虑简化前的问题怎么做：

若要计算 “经过若干次$y=m+1$，再经过若干次$y=-1$，再经过若干次$y=m+1$，再$...$” 的折线数量，则把起点$(0,0)$关于$y=m+1$对称，再关于$y=-1$对称，再关于$y=m+1$对称，再$...$ 所求折线数量即为 最终得到的起点到$(2n,0)$，不考虑是否经过某些直线的折线数量。

折线先经过$y=-1$的情况同理。

还是考虑容斥，容斥系数就是$(-1{)}^{对称次数}$

参考博客

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
const int mod=998244353;
int n,m,fac[N<<1],ifac[N<<1];
int C(int n,int m){
    
    
	return (ll)fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
int main(){
    
    
	scanf("%d%d",&n,&m);
	if(m>n){
    
    puts("0");return 0;}
	fac[0]=fac[1]=ifac[0]=ifac[1]=1;
	for(int i=2;i<=n*2;i++) fac[i]=(ll)fac[i-1]*i%mod,ifac[i]=(ll)(mod-mod/i)*ifac[mod%i]%mod;
	for(int i=2;i<=n*2;i++) ifac[i]=(ll)ifac[i-1]*ifac[i]%mod;
	int ans=C(n*2,n);
	for(int i=0,x=0;;i++){
    
    
		if(i&1) x=-2-x;
		else x=(m+1)*2-x;
		if(abs(x)>n*2) break;
		if(i&1) (ans+=C(n*2,(n*2-x)/2))%=mod;
		else (ans+=mod-C(n*2,(n*2-x)/2))%=mod;
	}
	for(int i=0,x=0;;i++){
    
    
		if(i&1) x=(m+1)*2-x;
		else x=-2-x;
		if(abs(x)>n*2) break;
		if(i&1) (ans+=C(n*2,(n*2-x)/2))%=mod;
		else (ans+=mod-C(n*2,(n*2-x)/2))%=mod;
	}
	printf("%d\n", ans);
	return 0;
}