提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档
文章目录
前言
本文是对于算法设计的相关习题。有错误，请不吝赐教。
一、第七章
对于某些物品分配给其他物体的情况，我们可以考虑用二部图中的匹配建模。（X中的节点代表工作，Y中的节点代表机器，此时的完美匹配为每一项工作分配到一台能够处理它的机器上，并且每台机器恰好分配到一件工作）
我们此章节考虑研究最大流问题，它包括了二分匹配这个特例，并且对于许多其他问题可以应用。
1.最大流问题与Ford-Fulkerson算法
流网络：图G=（V，E）
每条边e关联一个容量
存在单一源点s
存在单一汇点t
定义流：1.容量条件
2.守恒条件 fin(v)=fout(v)
剩余图：
前向边、后向边
增广路径：
考虑P是Cf中一条简单的s-t路径。
定义bottleneck（P，f）是P上任何边关于流f的最小剩余容量
augment(f,P)
令b=bottleneck（P，f）
for 每条边e 属于P
if e是一条前向边 then
fe增加b
else e是一条后向边
fe减少b
endif
endfor
return f
返回的值是一个新的流f’
Max-flow
对G中所有的e初始化fe=0
while 在增广图Gf中存在一条s-t路径
令P是Gf中的一条简单路径
f‘=augment(f,P)
把f更新为f‘
把增广图Gf更新为Gf'
endwhile
return f
由于流都为整数，所以可知流网络的上限为从s中出来的边的容量的和，我们认为该值为c。所以循环最多c次。
我们在构造剩余图时需要O（m）时间。找路径需要O（m+n）(DFS或者DPS），augment(f，P）用O（n）时间
O（mc）
具体的算法实现可见：
算法实现
2。网络中的最大流和最小割
上述的界C过于弱，所以我们考虑一个更好的上界。
割：s-t割是节点的划分，使得s属于A，t属于B，其容量为所有从A中出来的边的容量的集合。
s-t流f=fin(B)-fout(B)
从而我们得到了一个更好的上界——vf<=c(A,B) 其中A，B是s-t的任意割。
由此我们得到最大流=最小割。
通过已知最大流，我们可以构造剩余图Gf，执行宽度搜索，将所有从s开始能够到达的节点定义为A*，B*=V-A*，此时算法只需O（m）
3.选择好的增广路径
对于容量为实数的网络流，Ford-Fulkerson算法会出现多次迭代，从而降低算法的性能。
我们考虑如何去选择一个好的增广路径。
为此我们每一次选择有着至少△的瓶颈容量的路径。
Scaling Max-Flow
对G中所有的e初始化f(e)=0
初始化△为2的最大的幂，且不大于从S出来的最大容量
while △>=1
while 图Gf（△）有一条s-t的路径
令P是其中的一条简单s-t路径
f'=augment(f,P)
f=f'
更新Gf△
endwhile
△=△/2
endwhile
return f
△至多是C，不会小与1所以我们可知最多迭代1+log2C次。
可知每个缩放阶段的增广次数最多为2m
因此算法的时间为O（m^2 log2C）
补充：如果每次迭代选择具有最少边数的增广路径会导致一个强多项式的算法O（mn）
4.前向流推动最大流算法
通过将前向流转换为流。
前向流：破坏流节点的守恒条件。
前向流一致：1.ht=0，hs=n
2.对于剩余图中的所有边（v,w），我们有hv<=hw+1
我们可以证明如果s-t流与标记h是一致的那么在剩余图Gf中没有s-t路径，此时f为最大流。
push操作与relable操作
初始化 hs=n,ht=0
Push(f,h,v,w)
如果ef(v)>0 hw<hv 且（v,w）属于Ef
if e=(v,w) 是一条前向边 then
fe+=min(efv,ce-fe)
if e=(v,w)是一条后向边 then
fe-=min(efv,fe)
return f,h
relabel(f,h,v)
if efv>0 and 对于所有的边v,w，我们有hw>=hv
把hv+1
return f,h
初始化，对所有v令hv=0，hs=n
对所有e（s,v）令fe=ce,其他变为fe=0
while 存在一个节点v！=t 有efv>0
if 存在w使得push（f,h,v,w）可用 then
push
else
reblabel（r,h,v）
ednwhile
return f
我们可以证明所有节点最多被重新标记2n-1次。，并且标记的综述小与2n^2
改进：我们在每一步的选择中，选择有最大高度的节点。
实现思路：用表维护具有余量的点。对图采用邻接表表示。（链表维护前向边和后向边）current操作来知识当前节点。在重新标记节点v后，将指针重新放到第一条边。
5.应用：二分匹配：
对于二分匹配，我们考虑将图G加上两个点s,t。然后考虑给每条边设定容量为1.那么此时流的大小就是最大匹配的大小。
我们如果把流值为1的边的集合称为M，那么M的就可以看作是初始二部图G中的边集。
可以得到对应的算法时间为O（mn）
此时的增广路径也称为交替路径，作用是从匹配中取出所用的后向边，并用前向边代替它。
对于二分匹配是否存在完美匹配问题，我们可以这样考虑：
证明见p265
6.再有向与无向图中的不交路径
对于有向图：我们定义边的容量为1.
那么可以知道：
对于这v条路径，我们可以先找到一条路径，然后将该路径上的流改为0，在得到的f;上在去寻找剩下的v-1条，
如果遇到了圈，则将改圈上的边的流值改为0，然后再新的流f上去找剩下的v条。
此处可以考虑最大流与最小割的定理来证明。
对于无向图：
我们将无向图的边用两条有向边来代替。
此时我们可以考虑使用上述的Ford-Fulkerson来得到对应的流值，以及用上述的路径分解来得到对应的不交路径。
算法需要O（mn）
7.对最大流的推广：
最大流可以对许多具有主要组合搜索成分的问题在多项式时间内求解。
我们考虑带需求的流通问题：
我们类似上述的算法一样，添加一个超汇聚节点t和超源节点s、
类似的对于每个节点v（dv>0）我们添加一条边（v,t）容量为dv
类似的对于节点v（dv<0）添加边（s,v）容量为-dv
然后我们寻找一个最大流D的s-t流。
有可能我们对于流还会设置对应的下界。
我们在初始时令所以边的流的大小为它的下界，如果此时所有节点的需求以满足，那么得到解。否则，我们需要考虑增加容量来满足v的需求。
由此我们构造一个新的图，令容量为ce-le,节点需求为dv-Lv
我们有上面的思路来完成，如果这个图中有可行的流通那么就存在可行流通满足原图。
8.调查设计
问题描述：
我们考虑将所有的顾客定义为节点i，所有产品定义为j
其中如果顾客购买过j产品那么他们存在边，且改变的容量为1.
我们加入一个源点s和汇点t，用s来给每个用户节点i设值限制
用汇点来为每个产品设置限制。
对该图进行可行流的检查。
9.航线调度：
问题见P278
我们这样来分析问题：
我们将流的单位设置为飞机，且容量为1.（上下界都为1）
如果航班ui,vi 与航班uj vj是达的那么他们有一条具有容量1的边。
我们增加一个源点和汇点，其中（s,v）容量为1，（u,t）容量也为1
对于给定飞机数k，我们添加一条边（s,t）容量为k。（多余飞机不需使用）
此时给s一个-k的需求，t有一个k的需求。其他节点需求为0
（此时对于k’的流存在k条路径（每条边的容量为1），对每条路径分配一架飞机）
10 图像分割：
前景/背景分割（最小割）
罚分pij（相邻的两个节点一个为前景，一个为后景）
考虑一下式子达到最大。
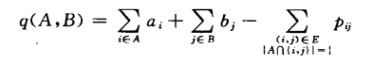我们创建汇点和源点来代表后景和前景。
此时我们考虑这个值的最大，这自然得到了求最大流的问题（求最小割）
11 项目选择
同样添加源点和汇点，将带正值的项目连接到s（可以认为需求是-v，或者点容量为v，此时也可看做fvin-fvout=-dv），负值连接到t。
此时同样考虑最小割算法。
12 棒球排除：
我们考虑给s,uxy gxy的容量，对于v,t m-wx的容量，给uxy vx gxy个容量。
13 对匹配问题增加费用？
每次迭代通过Dijkstra算法来找到s-t的最小费用路径。
然后对路径进行增广产生一个新的匹配M
找到M的一致价格
替换原先的匹配和价格
（一致价格？）
1.1 带解答的练习
1.1.1 练习1
由于时间是O（m+n）所以从头计算是不可能的。(从头计算需要O（mc））
由于某条边只加了一，所以我们在剩余图G‘中寻找增广路径。如果路径不存在，那么f就是最大流，否则进行增广操作，得到一个vf+1的最大流。
1.1.2 练习2
我们考虑网络流：
我们将一医生设为节点i，将日记设为节点j，对于每一个医生我们将它与可上班的日期连接。这条边的容量为1，同时将它与源点s相连，容量为c.同时我们把日期j与汇点t相连，每条边的上下界都是1。我们对源点设置-d需求，汇点设置d需求，然后判断是否有个可行的连通。
那么如何让医生最多为每个假期工作一天呢，我们在医生和假期间添加一个节点k，我们对于每个医生的假期j与k相连，同时将医生i与k的容量改为1.此时就做到了相应的限制问题。 同样找一个带需求的可行流通，
判断是否有流量为d的可行流存在。d为假期数。
图的构造可见下图：
1.2 课后练习
1.2.1 练习1
a)
{s,u,v} {t}
b)
4,每条边都为2，{s,v} {u,t}
1.2.2 练习2
a) 18
b)最大为21，考虑割为（s和最上部的顶点），其余顶点
1.2.3 练习3
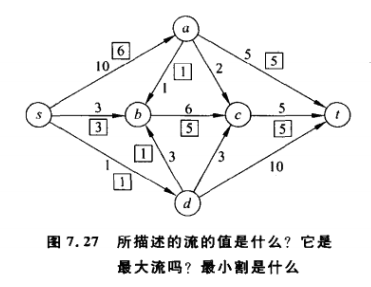a)这个流的值为10，不是最大流
b)最大割为{t,d} ,{s,a,b,c} 值为11
1.2.4 练习4
这是错误的
1.2.5 练习5
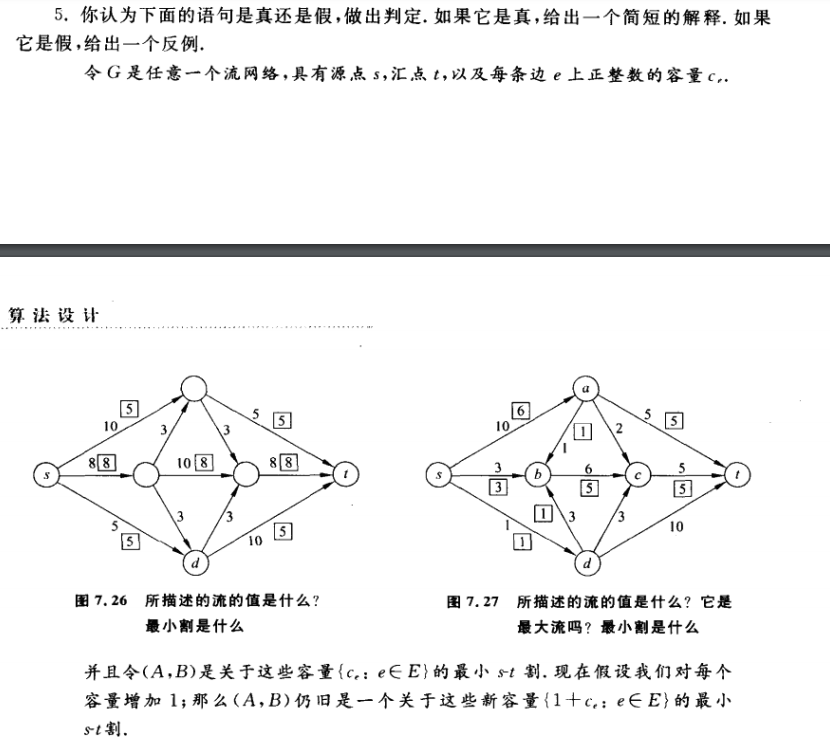错误，我们考虑图由节点S，v1,v2,v3,w,t 其中对每个i都有边（s,vi) (vi,w）,(w,t），我们考虑对于w,t 有容量4，其他的边为容量1，那么此时所有容量加1时，结论不成立。
1.2.6 练习6
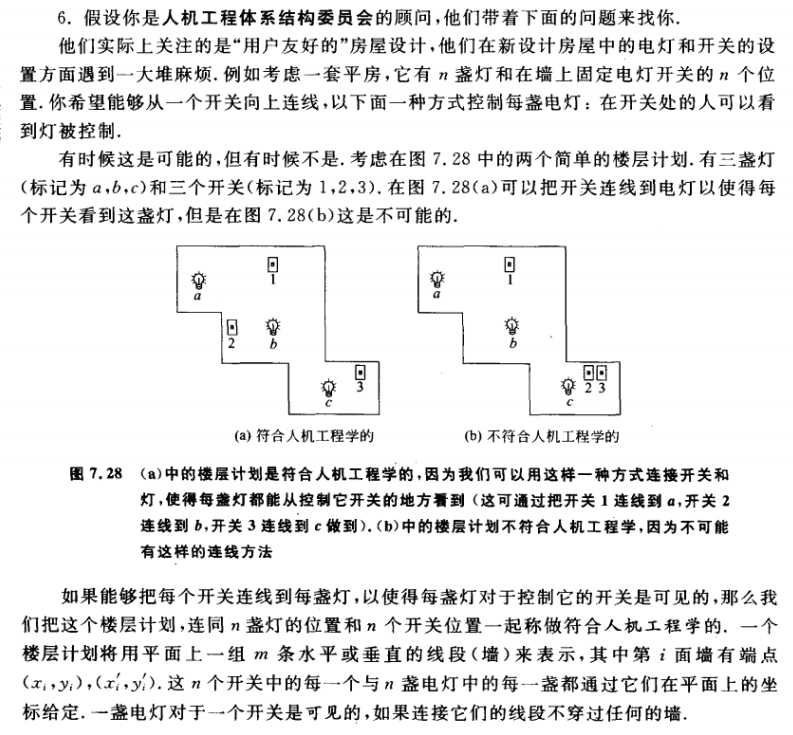
对于上述问题，我们考虑用二分匹配来解决这个问题
构造图G，其中将节点分为两个集合，其中X集合代表灯，Y集合代表开关。如果xi与Yj有边，那么意味着他们是能够可视的。
此时构造图的时间需要（n^2m）
我们可以发现如果这个构造是符合人机工程学的，那么必定有一个对应的完美匹配。
所以我们这里可以考虑用二分匹配算法来完成。具体的可见上述的二分匹配部分内容。
1.2.7 练习7
这里我们同样考虑网络流算法，具体构造图如下，
我们增加汇点t和源点s，将客户看做节点i，基站看做节点j
如果用户和基站相差不超过r那么这两者之间存在一条边且容量为1，源点与i相连，容量为1，基站j与汇点相连，容量为L。
我们对源点s需求定为-n，汇点t定为n，看是否存在上述可行的流。
1.2.8 练习8
a)我们考虑带有需求的网络流算法。我们考虑这样构造图结构：我们将已有的血型设为节点i，需求的血型设为节点j，在图中增加源节点s和汇点t。将源点s与i相连，容量为各自的现有量，将i与j相连如果这两者能够适配的话，容量为需求的量，同时将j与t相连，边的容量为需求的量。
我们考虑是否存在流量为需求量的总和的流存在。
b)
我们考虑一个最小割（s,a,b） 此时他的容量为50+36+10+3=99，所以无法满足。
我们可以知道无法满足，对于A型血和B型血以及O型血无法满足。
我们考虑采用贪心策略：
具体策略如下，我们先满足考虑先满足O，在满足A,B最后满足AB。
1.2.9 练习9
考虑网络流算法，我们构造图G如下：
对于每一个病人设为节点i，对于每一家医院设为节点j，另外再加上一个源点s，汇点t，病人i如果能够被送到医院j那么有边(i,j),容量为1，每家医院到汇点t的容量为n/k，源点到病人i的容量为1.
算法需要O（n+k）个节点 以及O（nk）边
算法时间O（n^2*klogn）
构造图需要（n^2k）时间
我们考虑该图中是否存在为n的流。
1.2.10 练习10
我们这样考虑，假如减少容量的边在流中不饱和，那么不产生影响。
否则我们需要恢复节点的守恒条件，我们沿着w-t上的路径的边的容量都减少1，同样对于v-s上的路径的边都减少1，在考虑修改后的剩余图，如果不存在增广路径那么修改后的流f1就是最大流，否则得到增广后的流f，此时f与原先的流相同，此时它只可能是最大流。
1.2.11 练习11
1.2.12 练习12
二、第八章 NP与计算难解性
1.多项式时间归约
如果能够用多项式个标准的计算步骤加多项式次调用解问题X的黑盒子来解问题Y的任意实例，那么我们认为Y<=Px
即Y多项式时间可归约到X，此时y也可以在多项式时间内运行。
（之前的求解二分匹配问题等）
2.第一个归约 独立集和顶点覆盖：
独立集：给定图G和数k，问G包含大小至少为k的独立集吗？
顶点覆盖：给定图G和数k，问：G是否包含大小至多为k的顶点覆盖？
证明如下：考虑顶点覆盖V-S，此时S就是一个独立集，因为S中的任意两个端点，如果它们有边e，那么e的两个端点都不在V-S中，与顶点覆盖定义冲突。反之亦然，
我们可以证明独立集<=P顶点覆盖 （独立集大小最大为k时，顶点覆盖大小最小为N-k）
顶点覆盖<=P独立集
3.从顶点覆盖到集合覆盖：
集合覆盖：
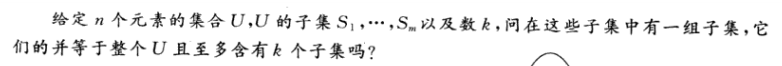可证明：顶点覆盖<=P集合覆盖
证明：我们考虑全集U为边集E。子集为si（节点i所覆盖的边）
这就可以证明将顶点覆盖改造为集合覆盖然后调用集合覆盖的黑盒子，就可得解。
这里给出了一个归约方法，将X的实例变为Y的一个实例，调用Y的黑子进行解答（X<=Py）
类似的我们可以证明独立集<=P集合包装
集合包装（进程冲突）：
4.使用零件归约：可满足性问题
SAT（可满足性问题）：
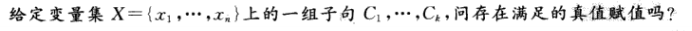满足存在值使得合取为1.
3-SAT（三元可满足性）：每个子句长为3.
补充：可满足性与三元可满足性是基本的组合搜索问题：必须做出n个独立的决定，使得满足一组约束条件。有多种方法单独的满足每一个约束，但需要所有约束同时满足
3-SAT归约到独立集：
方法：对于归约Y<=PX,用问题X中的分量构造零件来描写问题Y中正在做的事。
证明：3-SAT<=P独立集
我们考虑有一个独立集的黑盒子。
思路：从每一个子句中选择一个项，然后找一个真值赋值使得所有这些项都为1.从而满足所有的子句。如果没有两个被选中的项冲突，那么就成功。
冲突：一个项等于变量xi,另一个项等于它的否定。
我们考虑构造图G，如下图所示：
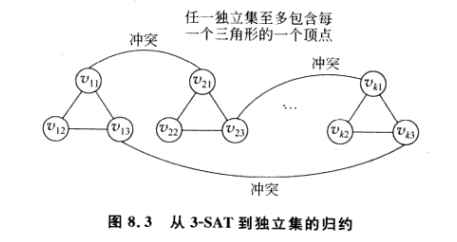对于独立集的概念，我们可知对于每个三角形我们只能选择一个项赋值给1。同时我们在冲突的项的顶点之间添加边。
此时我们将3-SAT的实例改变到了一个独立集的实例。
由此我们得到可以将3-SAT归约到独立集。
归约具有传递性：
Z<=pY 且 Y<=pX 那么 Z<=pX
4.有效证书和NP的定义
验证程序：算法B是有两个输入变量s和t的多项式时间算法，具有多项式p，使得对于每一个输出串，当且仅当存在串t使得t<=p|s|且使得B（s,t）=yes
这表明有效验证程序更愿意去评估提交的证据t，来判断。
NP是所有存在有效验证程序的问题的集合。（三元可满足问题、独立集问题、集合覆盖问题等）
5.NP完全问题
对于NP完全问题的定义：
X属于Np，对于所有的Y属于NP，Y<=pX
如果X是一个NP完全问题，那么X在多项式时间内可解当且仅当p=Np
第一个NP完全问题电路可满足性：
我们考虑电路K是一个带标号的有向无圈图。其中K中源节点的标号为常数0/1或不同的变量名。我们把这些看做是电路的输入。
其他的节点标有不同的布尔运算。存在唯一一个不带离开边的节点，它表示输出。
具体图见下：
电路可满足性的问题如下：给定一个电路，需要确定是否存在对输入的赋值使得输出值为1.
对于电路可满足性是NP完全问题的证明思路：考虑X<=P电路可满足
我们考虑长度为n的输入sn与验证t。那么我们可以将前n个节点设计为n个输入，后面的节点认为是t的输入。那么此时就变成了一个电路可满足问题，归约也就完成。
有了一个NP完全问题剩余的就会非常简单。
我们考虑证明三元可满足是NP完全的。
我们可以将其的正值赋值来归约到电路可满足性来证明。
给定电路可满足性的一个实例，我们构造一个等价的3-Sat实例来证明
具体构造如下：
上述也就完成了Sat实例的构造，那么如何构造3-SAT呢？我们做一下步骤。
同样根据之前的归约我们可以得到以下结论：
由此我们得到了证明新NP完全问题的通用策略：（cook归约）
1.证明X属于NP
2.选择一个已知的NP完全问题Y
3.证明Y<=pX
我们也可以通过一个变换，将给定的Y实例变成X的一个有相同答案的实例。具体如下：（Karp归约）
6.排序问题
我们在这里考虑一个著名的排序问题巡回售货员问题。
问题描述如下：
判定形式如下：
对于巡回售货员问题有一个基于图的类似的问题即哈密顿圈问题。
哈密顿圈问题：给定一个有向图G=（V,E），如果图G中的圈C恰好经过每一个顶点一次，则称圈C是一个哈密顿圈。
我们考虑证明哈密顿问题是NP完全的。
证明如下：我们可以知道哈密顿圈属于NP，因为有一个多项式的时间内能够确定该顺序包含所有顶点一次。
我们现在证明哈密顿圈问题是NP完全的。我们考虑3-SAT<=P哈密顿圈
我们考虑一个任意3-SAT实例，他有变量x1,x2,xn和子句c1.。。ck
补充：3-sat的本质是我们想令变量为什么值就可以令它为什么值，同时每个子句有三个机会满足。
我们考虑一个有2^n条哈密顿圈的图开始，这些哈密顿圈自然的对应与变量的2 ^n 个真值赋值。
我们接着构建n条路径p1.p2…pn，添加源点s和t，最后得到图的结构如下，可知共有2^n条哈密顿圈。
这就很自然的对应了3-SAT实例中的变量x1,xn赋值的n种独立选择
我们假设如果从左到右通过Pi，那么令xi等于1否则等于0
我们现在需要模拟子句C
我们考虑将ci插入到对应路径中具体如下：
由此我们便证明了如果3-SAT实例是可满足的当且仅当G有哈密顿圈。
由此证毕。
我们现在考虑巡回售货员问题，很明显该问题是属于NP的，同时我们可以知道哈密顿圈<=p巡回售货员。归约思路：考虑有向图G，给定每条边为1，无边则为2，所以G有哈密顿圈当且仅当巡回售后员实例中有长度不超过n的巡回路线。
7.划分问题
三维匹配问题：类似于二部图匹配，我们考虑三维匹配。
具体问题描述如下：
三维匹配问题可以看做是集合覆盖和集合包装的特殊情况。
我们考虑证明三维匹配是NP完全的.很容易知道存在一个多项式时间的验证算法是使得三维匹配问题是NP的。
对于证明三维匹配问题是NP完全的，我们还是用3-SAT实例来完成。
我们考虑一个3-SAT实例。我们先设计零件来表示对于每个变量的独立选择。然后通过添加零件来表示子句的约束。
我们如下规定:考虑零件的核心Ai={ai1，ai2,ai3…ai,2k}
零件的边梢：Bi={bi1,bi2,bi2k}
三元组tij=（aij，aij+1,bij）
我们考虑智能选择零件i中的所有偶三元组或者奇三元组，如果选择偶三元组那么令xi=1.
我们依旧考虑子句C如下：
但是以上的覆盖会留下一些边梢未被覆盖。由此我们添加消除零件，来添加对应的边梢。以此保证所有都被覆盖。
那么这样我们就构造了一个三维匹配的实例。证明完成。
8图着色问题：
任给定图G和界限k，问G是否有k着色？
图着色问题很自然的能够应用在如下实践中：
1.考虑工序的无冲突安排
2.分配寄存器
3.无线交换设备的波长分配
我们现在需要证明三着色问题是NP完全的
我们容易证明该问题是NP的。
类似于其他问题，我们同样考虑用3-SAT来证明它。
考虑用真节点，假节点和基点来构造图。
构造如下：
具体证明见p345
9.数值问题
子集和问题
我们之前讨论过这个问题，利用动态规划来求解。得到的时间复杂度为O（nW），在W较小时是合理的，但如果W较大时就变的不合理了。
所以我们之前得到的算法回一个伪多项式算法
证明子集和是NP完全的。
我们在这里考虑利用三维匹配来证明。
主要思想是利用整数加法来表示集合运算。（集合的并，同时不进位）
由此我们可以得到以下结论：
10.co-np 和np的不对称性
从上述我们可以知道有效证书的定义根本是不对称的，NP的定义也是不对称。
我们考虑co-NP:问题X属于co-NP当且仅当它的补问题X属于NP。
如果一个问题既属于NP又属于co-NP，那么当答案是yes时，有个短证据，同样，no时也有短证据。
（二部图完美匹配）
11难问题的部分分类
1.包装问题
给定对象的集合，要从中至少选择k个，同时对象之间有冲突，某些对象无法选择。
基本的包装问题:
独立集：给定图G和数k，问G有大小至少为k的独立集吗？
集合包装：给定n个元素的集合U，U的子集S1.。Sn和数k，问这些子集中至少有k个两两不相交吗？
2.覆盖问题
给定一个对象的集合，要选择一个子集，合起来达到一定目标。
基本的覆盖问题：
顶点覆盖：给定图G和数k，问G有大小不超过k的顶点覆盖
集合覆盖：给定n个元素的集合U，U的子集S1.。。Sn和数k问这些子集中有不超过k个的并等于整个U的吗？
3.划分问题：
划分为题将对象集合分成子集的所有方式，要求每一个对象恰好出现在一个子集中。
三维匹配
图着色：
4.排序问题：
在一组对象的所有排列上进行搜索
哈密顿圈
哈密顿路径
巡回售货员
5.数值问题
该问题的困难性主要在于子集和。
子集和：给定自然数W1.。Wn 和目标W问是否有一个子集加起来恰好等于W。
6.约束满足问题
电路可满足，SAT，3-SAT
对于设计3-SAT归约时：
1看做搜索变量的赋值，要求所有子句都必须满足
2看做搜索从每一个子句中选择一项让它满足的选择方式
2.1 带解答的练习
2.1.1 练习1
我们现在需要找一个已知的NP完全问题并归约到可疑集团。我们考虑用顶点覆盖或者集合覆盖归约它。
我们把顶点覆盖归约到这个问题。
假设顶点覆盖实例中的图G由m条边，其中ej=（vj,wj）如下构造可疑集团的实例。对于G的每一个顶点构造使用者，对每一条边构造一个分钟t。在t分钟，与ej两个端点相关的使用者访问IP地址it。
2.1.2 练习2
