一、前置知识

同态加密以及全同态在另一篇文章中已经说的非常详细了：

同态加密的原理详解与go实践

同态加密与全同态加密的原理公式表示如下:

$f(m_1,m_2,m_3, ...) = D(f(E(m_1),E(m_2), E(m_3), ...))$

若 $f(m_1,m_2,m_3, …) $存在有效的加法运算或乘法运算，称该加密算法支持半同态加密;若存在有效的加法运算和乘法运算，称该加密算法支持全同态加密

二、DGHV算法构建

思路：通过对称加密改进出一种非对称/公钥加密算法

对称加密方法

定义一套对称加密方法：

$keyGen(\lambda)$ 根据安全参数 $\lambda$ 生成一个大奇数 $p$ 密钥, $\eta \ （bit）$ 是生成密钥 $p$ 的位数

$E n c r y p t o (p k, m)$ 表示加密,其中 $p k$ 表示公钥, m是明文，根据Dijk中的规定 $\in \{0,1\}$ 也即明文m只有一位;

$r, q$ 都是正随机数, 长度分别为 $\rho、 \gamma$ , 其中的要求是 $q > p$ 且 $q$ 是公开的 , $r$ 是一个随机小整数（可为负数）

则加密过程为:
$E n c r y p t o (p k, m) = m + 2 r + p q$
对应的解密过程 $D e c r y p t o (s k, c)$ , 其中 $s k$ 表示私钥、 $c$ 表示密文:
$\ mod \ p) \ mod \ 2 = （c - p* \ulcorner\dfrac{c}{p}\lrcorner）mod \ 2 = Lsb(c) \ XOR \ Lsb(\ulcorner\dfrac{c}{p}\lrcorner)$

扫描二维码关注公众号，回复： 13214282 查看本文章

约定：

一个实数模 $p$ 为: $\ mod \ p = a - p * \ulcorner\dfrac{a}{p}\lrcorner$ ，其中 $\ulcorner x\lrcorner$ 表示** $x$ 的最近整数**，即有唯一整数在 $(x-\frac{1}{2}, x+\frac{1}{2}]$ 范围中，所以 $\ mod \ p$ 的范围就是 $(-\frac{p}{2}, \frac{p}{2}]$

注意这里的取模与一般的取模的不同，一般的取模计算是向下取整 $\left\lfloor\dfrac{a}{p}\right\rfloor$ ，范围也就是 $[0, p - 1]$
$L s b$ 是最低有效位，因为最后是模2运算，所以结果就是这个二进制数的最低位

很多学者将这里的加解密的2替换为 $2^k$ 使之能适应k位的明文

注意：这里是对称加密，所以公钥和私钥是相同的，即 $p k = s k = p$ 

正确性的验证：

对于解密算法显然可以看出 $\ p$ 将 $p q$ 项消除， $m o d 2$ 将随机数 $r$ 项消除，最后的结果就是 $m$

公钥加密方法

通过上面的对称加密, 下面考虑将其改造成为一个公钥算法：

直接将 $p q$ 看作是公钥，但是因为随机数 $q$ 是公开的，所以私钥 $p$ 立即就会被知晓，这样是不安全的

可以通过使用私钥生成一系列零密文(输入为0)的方式来生成公钥：

$pk_i = Encrypto(sk,0) = 2r_i + pq_i$

可以将上面的公式运行的结果做成一个集合即： ${x_i;x_i=2r_i+pq_i\}$ , 公钥 $p k$ 就是这个集合 ${x_i\}$

加密时从 ${x_i\}$ 中选取一个子集记为 $S$ ，则按如下公式进行加密:

$E n c r y p t o (p k, m) = m + 2 r + s u m (S)$ 其中 $s u m (S)$ 表示对 $S$ 中的 $x_i$ 求和

由于 $s u m (S)$ 是一些0的加密密文的和，所以对于解密来说并无影响，所以解密过程不变

观察上面生成 $pk_i$ 的式子，不管在其后添加多少这样的式子，解密时都会被求余消去

如此就可以得到如下密钥对：

公钥: $\subseteq \{xi\}$
私钥: $p$

安全性

1. 已知明文长度攻击

当攻击者事先知道明文的长度时, 在数位较少时, 可以直接猜想每一个位(50%的正确率)

所以一般采用大整数的方式，防止类似的攻击

2. 已知密文攻击

抛开其中的随机数 $r$ (噪音) 不谈，DCHV的安全性主要依赖于数学困难问题—“近似GCD问题”

简单来说，给出一系列 $x_i$ ，无法在有效的时间内解得 $p$ , 因为根据 $x_i=2r_i+pq_i$ ，所以 $x_i$ 可以看作是一系列近似 $p$ 的倍数，通过一系列近似 $p$ 的倍数求 $p$ 的过程就是近似最大公约数问题(approximate—GCD problem),目前还是计算困难的

噪音的干扰

由于公钥是公开的，所以知道密文c之后就可以减去公钥得到： $c - p k = m + 2 r$ (可以把 $p k$ 看作是 $p q$ )

由于存在 $r$ 的干扰，所以无法识别明文m, 所以 $m + 2 r$ 就称为噪音

噪音是能否正确解密的关键！

当 $\ mod \ p = m+2r \leq \frac{p}{2}$ 时，再进行模2运算可以得到正确的明文m即 $\ mod \ 2 = m$ 成立
当 $\ mod \ p = m+2r > \frac{p}{2}$ 时，第一步模 $p$ 运算就会失败，结果不在等于 $m + 2 r$ ，后面再模2自然也解密失败

为何是以p/2为标准？因为求余采用的最近整数其范围就是 $(-\frac{p}{2}, \frac{p}{2}]$

同态性证明

假设密钥为 $p$ ，1位的明文 $m_1,m_2$ ，则有:

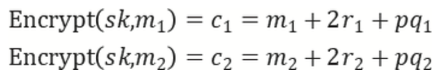
同态加法

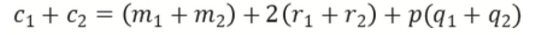
$Decrypto(sk, (c_1+c_2)) = m_1 + m_2$

满足加法同态

同态乘法

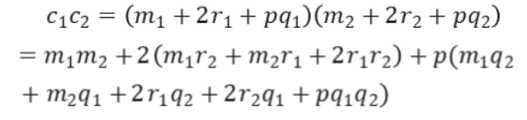
$Decrypto(sk, (c_1c_2)) = m_1m_2$

在噪音影响范围内满足乘法同态（不理解见下文分析）

噪音分析

加法的噪音： $(c_1+c_2) \ mod \ p = (m_1+m_2) + 2(r_1 + r_2) $

乘法的噪音: $ c_1c_2 \ mod \ p = m_1m_2 + 2(m_1r_2+m_2r_1+2r_1r_2)$

可知：密文之和的噪音是各自密文的噪音之和,而密文乘积的噪音是噪音之积

所以在同态乘法中运算，噪音会被放到很大

一个例子：

对密文运算会造成噪音的增大，当噪音超出范围，解密就失败，这意味着对密文运算不可能是无限次的

所以可以得出结论：

此方案是类全同态方案，因为噪音的原因只适用于少量的加密计算

推广

这两部分目前本人也在学习中。。。所以后续再更新

1. 真-全同态加密

类全同态不是我们想要的结果，我们要实现的是真的全同态加密方案：

已有的思路：密文刷新

既然噪声会不断的扩大，那么就在中途将其刷新，即每次在对密文运算之前先将密文进行解密，就会得到一个新鲜的密文，这个噪音是很小的，然后再对密文做运算，就可以保证其同态性（当然计算复杂度也提升了很多）

2. 加解密电路

有了基础比特的同态运算，结合类似电路组合可以实现多种算术上的同态

学习资料来源

论文：《一种基于智能合约的全同态加密方法》

知乎：https://zhuanlan.zhihu.com/p/71583737

http://blog.sciencenet.cn/blog-411071-617182.html

[1] M. Dijk, C. Gentry, S. Halevi, and V.Vaikuntanathan. Fully homomorphic encryption over the integers[J]. Applications of Cryptographic Techniques: Springer, Berlin, 2010, 24-43.

觉得不错的话，请点赞关注呦～～你的关注就是博主的动力
关注公众号，查看更多go开发、密码学和区块链科研内容：
2DrbmZ

DGHV:整数上的同态加密(1)-算法构建