本系列是七月算法机器学习课程笔记
文章目录
1 不同类型的学习
机器学习:监督学习、无监督学习、强化学习
按照问题类型分:
聚类问题:相似用户分析、新闻聚类
分类问题(选择题) 情感分类、垃圾邮件、图像内容与识别
回归(回答类问题) 房价、票房值、
强化学习:研究如何根据环境而行动
2 基本术语与概念
数据集:训练集、测试集
样本=示例=样例
特征 属性、属性值
属性空间 样本空间
特征向量
标记 label 输出空间
3 线性回归模型
3.1 什么是线性回归
有监督 学习,输出是连续值
假定输入与输出之间是线性关系:f:x->y
例如体重与身高可能就是线性关系,房屋的价格与面积是线性关系
单变量线性回归: f = a x + b f=ax+b f=ax+b
多变量线性回归: f ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 = ∑ i = 0 n θ i x i = θ T X f(x)=\theta_0+\theta_1x_1+\theta_2x_2=\sum_{i=0}^n\theta_ix_i=\theta_TX f(x)=θ0+θ1x1+θ2x2=∑i=0nθixi=θTX
3.2 损失函数
数据驱动=数据+模型
模型=假设函数
当数据确定的时候,x将不再是未知数,而参数是未知数,所以方程可以写为: h ( θ ) = ∑ i = 0 n θ i x i h(\theta)=\sum_{i=0}^n\theta_ix_i h(θ)=∑i=0nθixi
损失函数
在监督学习中优化=损失函数 + 优化算法
我们要找到最好的参数 θ \theta θ,如何衡量呢?用损失函数定义
损失函数:定义了当前状况下与标准答案差异情况的函数。
J ( θ 0 , θ 1 , θ 2 . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1,\theta_2...\theta_n)=\dfrac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1,θ2...θn)=2m1∑i=1m(hθ(x(i))−y(i))2
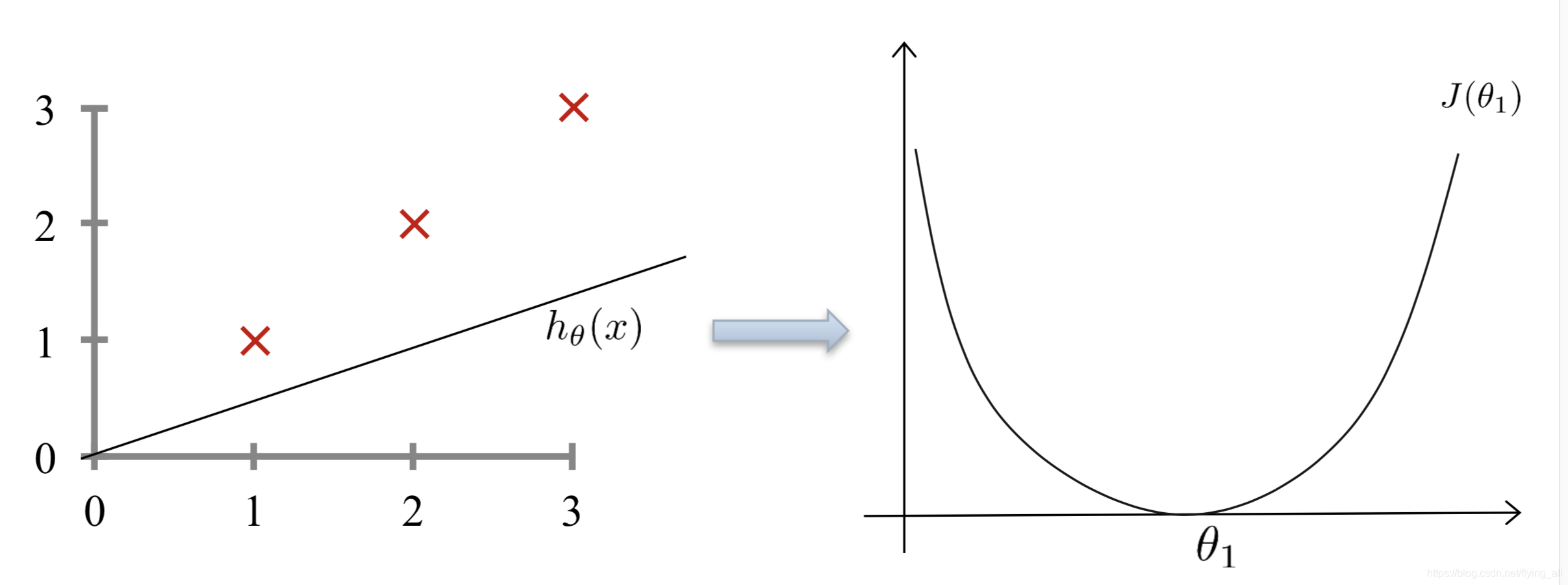
3.3 最小化损失函数-梯度下降
损失函数是一个凸函数, J ( θ 0 , θ 1 , θ 2 . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(\theta_0,\theta_1,\theta_2...\theta_n)=\dfrac{1}{2m}\sum_{i=1}^m(h_\theta(x^i)-y^i)^2 J(θ0,θ1,θ2...θn)=2m1∑i=1m(hθ(xi)−yi)2
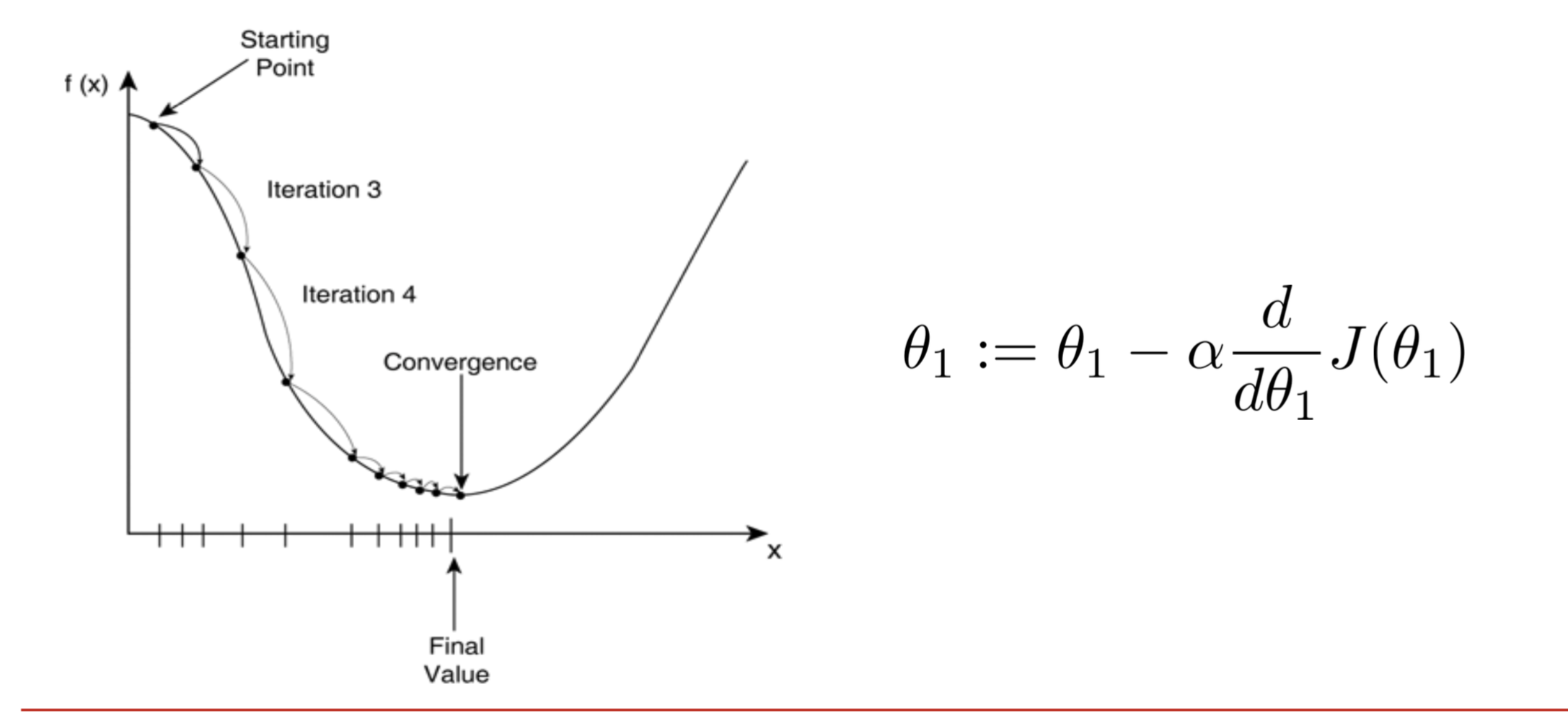
可以使用梯度下降的方式找损失函数的最小值。这就如同将一个小球在一个碗里,让它滚落到碗底。这里涉及到两个问题:一个是最开始小球放哪:初始位置,另外一个是小球从哪个方向滚。
初始位置不重要,放哪里都行。
滚的方向:在一条曲线中变化最快的方向是梯度方向,在开始点梯度方向是函数值增加的方向,所以滚的方向是负梯度方向。(这块内容需要用数学补充)
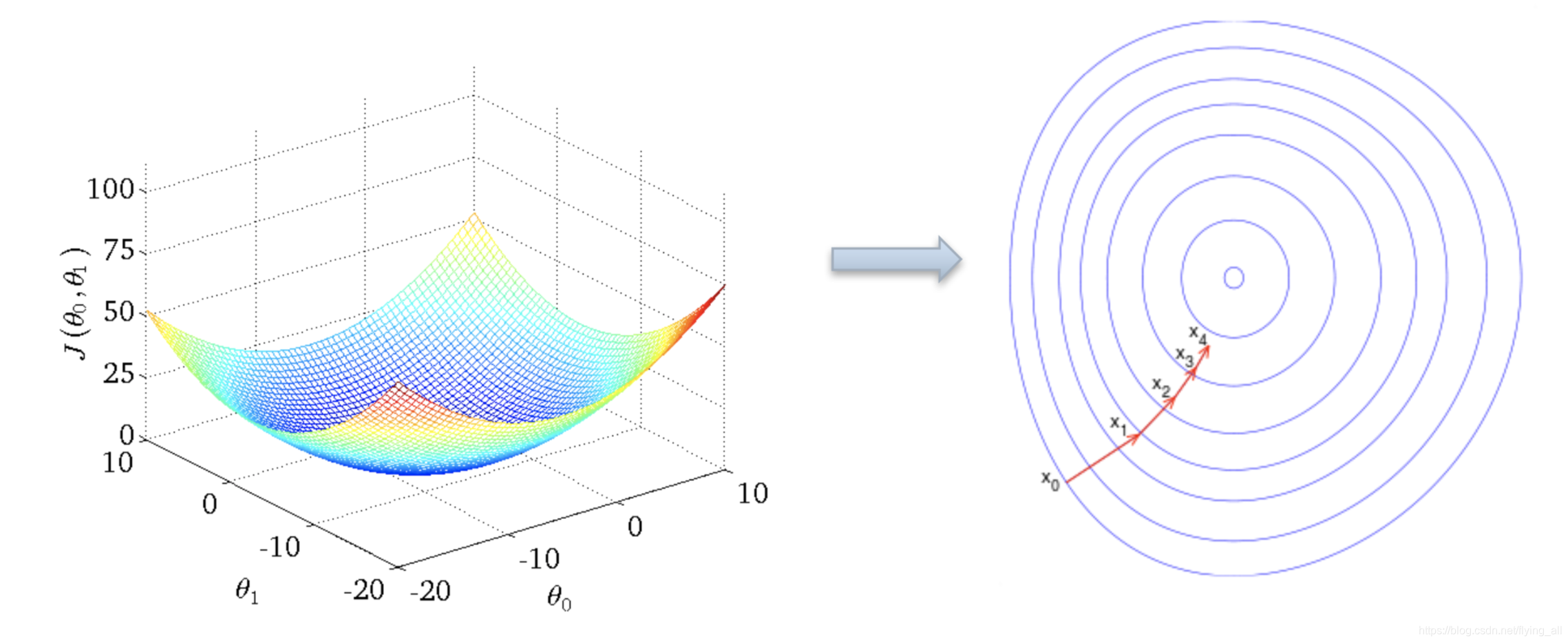
在多维情况下 梯度方向垂直于等高线。每次迈进一小步,直到山底。
参数迭代函数:
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \theta_0 :=\theta_0 -\alpha\dfrac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)}) θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) . x 1 ( i ) \theta_1 :=\theta_1 -\alpha\dfrac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)}).x_1^{(i)} θ1:=θ1−αm1∑i=1m(hθ(x(i))−y(i)).x1(i)
3.4 学习率有什么影响
学习率小,梯度下降慢,训练时间长
学习率大,会跨越最低点,形成振荡
3.5 过拟合与欠拟合
欠拟合:模型参数不够,表现不好。类似于一个孩子智商不够,学习不好一样。
过拟合:模型参数太多,不用学习,只是记忆答案,但遇到新的问题就不会了。类似于一个孩子智商太高,背会了所有练习题的答案。但是不会做新题。
对应的解决方法是:正则化
正则化:用来控制参数 θ \theta θ的幅度, 限制参数 θ \theta θ的搜索空间。这样损失函数就变成了: J ( θ 0 , θ 1 , θ 2 . . . θ n ) = 1 2 m ∑ i = 1 n ( h θ ( x i ) − y i ) 2 + λ 2 ∑ j = 1 n θ j 2 J(\theta_0,\theta_1,\theta_2...\theta_n)=\dfrac{1}{2m}\sum_{i=1}^n(h_\theta(x^i)-y^i)^2+\dfrac{\lambda}{2 }\sum_{j=1}^{n}\theta_j^2 J(θ0,θ1,θ2...θn)=2m1∑i=1n(hθ(xi)−yi)2+2λ∑j=1nθj2
4 逻辑回归
4.1 为什么要有逻辑回归
现在问个问题是:希望根据肿瘤大小,判断病人是否患有癌症。
根据线性回归建模:可以设置阈值0.5,根据这个阈值算出一个肿瘤大小的分割线。
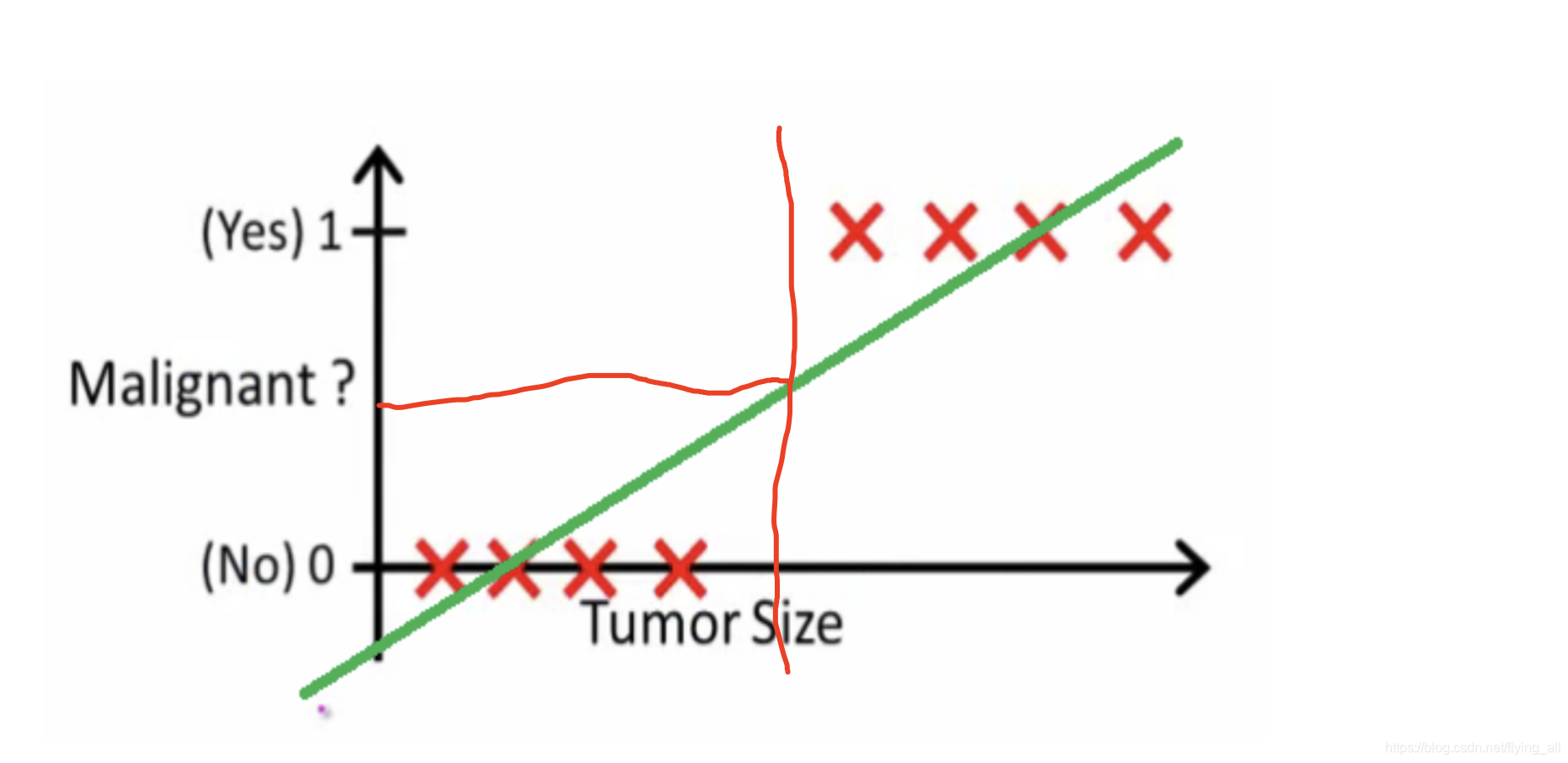
上面看似没有问题。如果有一些肿瘤尺寸很大的样本加入之后,这条线的斜率发生变化。此时再以0.5作为阈值,那么有些样本就会被错误的分类。也就是说线性回归用于分类问题的时候,特征值的范围会严重影响分类效果。

4.2 什么是逻辑回归
神奇的sigmoid函数:sigmoid函数也叫s曲线。
S ( x ) = 1 1 + e ( − x ) S(x)=\dfrac{1}{1+e^{(-x)}} S(x)=1+e(−x)1
它的导函数是 S ( x ) ′ = S ( x ) ( 1 − S ( x ) ) S(x)'=S(x)(1-S(x)) S(x)′=S(x)(1−S(x))
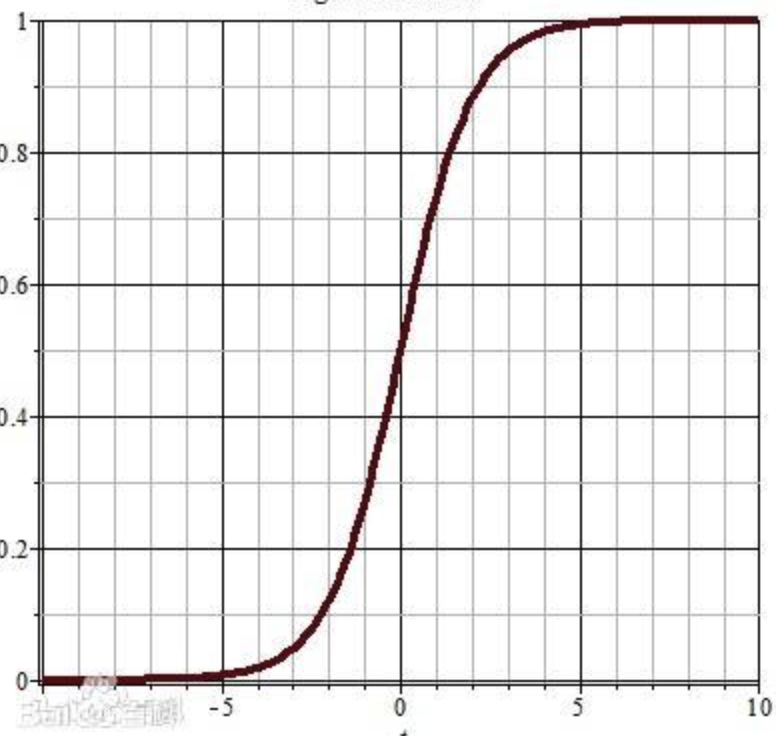
sigmoid函数能够把任意值转换到(0,1)范围内。我们可以将上面线性回归模型计算的值,作为入参送入sigmoid函数,得到一个(0,1)范围的值。
4.3决策边界
所有分类问题都是要找到一条决策边界。怎么用线性回归找到可以拟合出决策边界呢?
线性边界判定
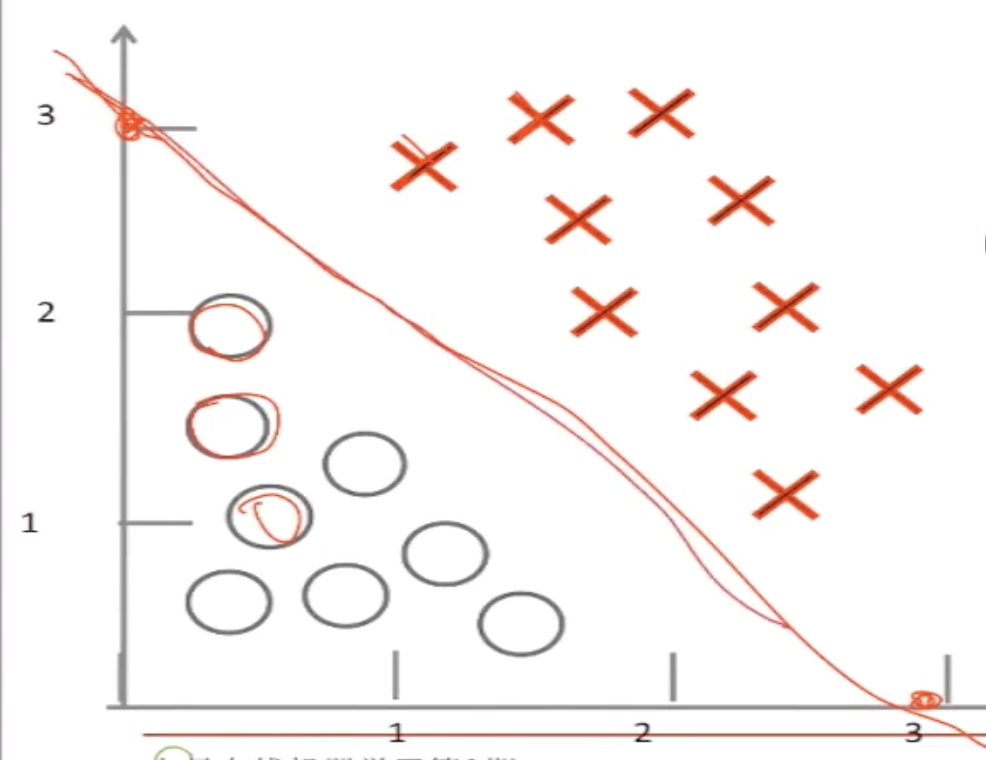
假设函数 h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2) hθ(x)=g(θ0+θ1x1+θ2x2),假定 θ 0 = − 3 \theta_0=-3 θ0=−3, θ 1 = 1 \theta_1=1 θ1=1, θ 2 = 1 \theta_2=1 θ2=1,那么当 − 3 + x 1 + x 2 > 0 -3+x_1+x_2>0 −3+x1+x2>0的时候,所有的点是在直线上方的,再看sigmoid函数,当输入值>0的时候,值是>0.5的。那么就可以理解图中x的概率是>0.5的。同理,图中圆圈的概率是<0.5的。我们就可以基于0.5给出一条决策边界。
非线性边界判定
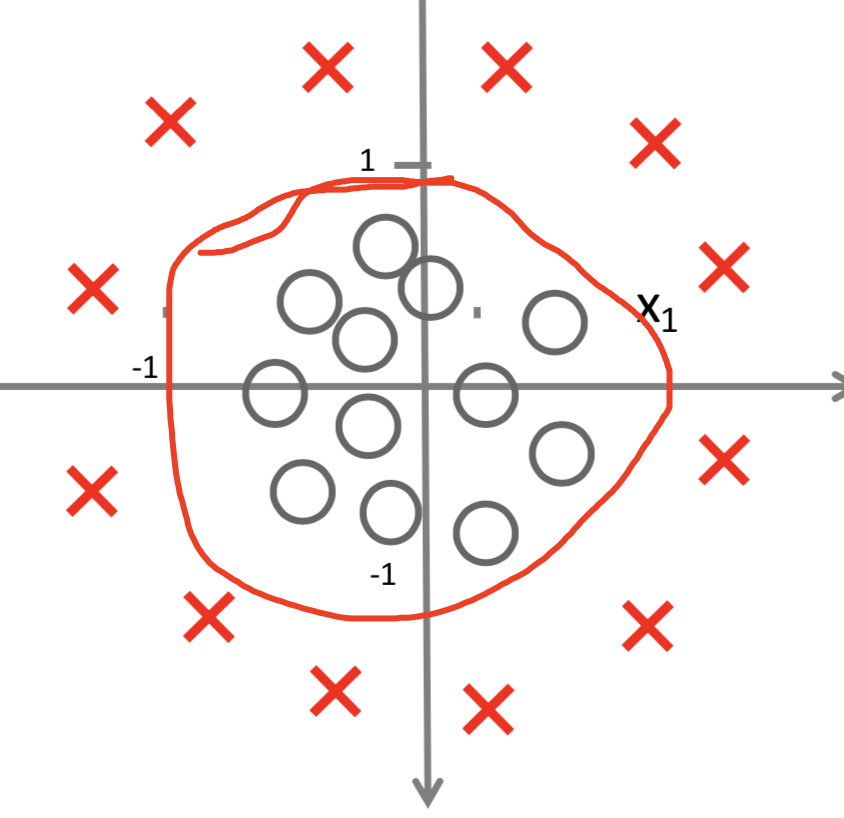
假设函数 h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22),假定 θ 0 = − 1 \theta_0=-1 θ0=−1, θ 1 = 0 \theta_1=0 θ1=0, θ 2 = 0 \theta_2=0 θ2=0, θ 3 = 1 \theta_3=1 θ3=1, θ 4 = 1 \theta_4=1 θ4=1,也就是说函数变为: h θ ( x ) = g ( − 1 + x 1 2 + x 2 2 ) h_\theta(x)=g(-1+x_1^2+x_2^2) hθ(x)=g(−1+x12+x22)。对于 x 1 2 + x 2 2 − 1 = 0 x_1^2+x_2^2-1=0 x12+x22−1=0可以形成这样一条圆形的曲线。 x 1 2 + x 2 2 − 1 > 0 x_1^2+x_2^2-1>0 x12+x22−1>0表示圆外面的x点, x 1 2 + x 2 2 − 1 < 0 x_1^2+x_2^2-1<0 x12+x22−1<0表示圆内的○点。将其送入sigmoid函数,可以得到对应的概率。
4.4 损失函数
在逻辑回归中使用同样的损失函数发现好多凹凸点,不再是个凸函数。
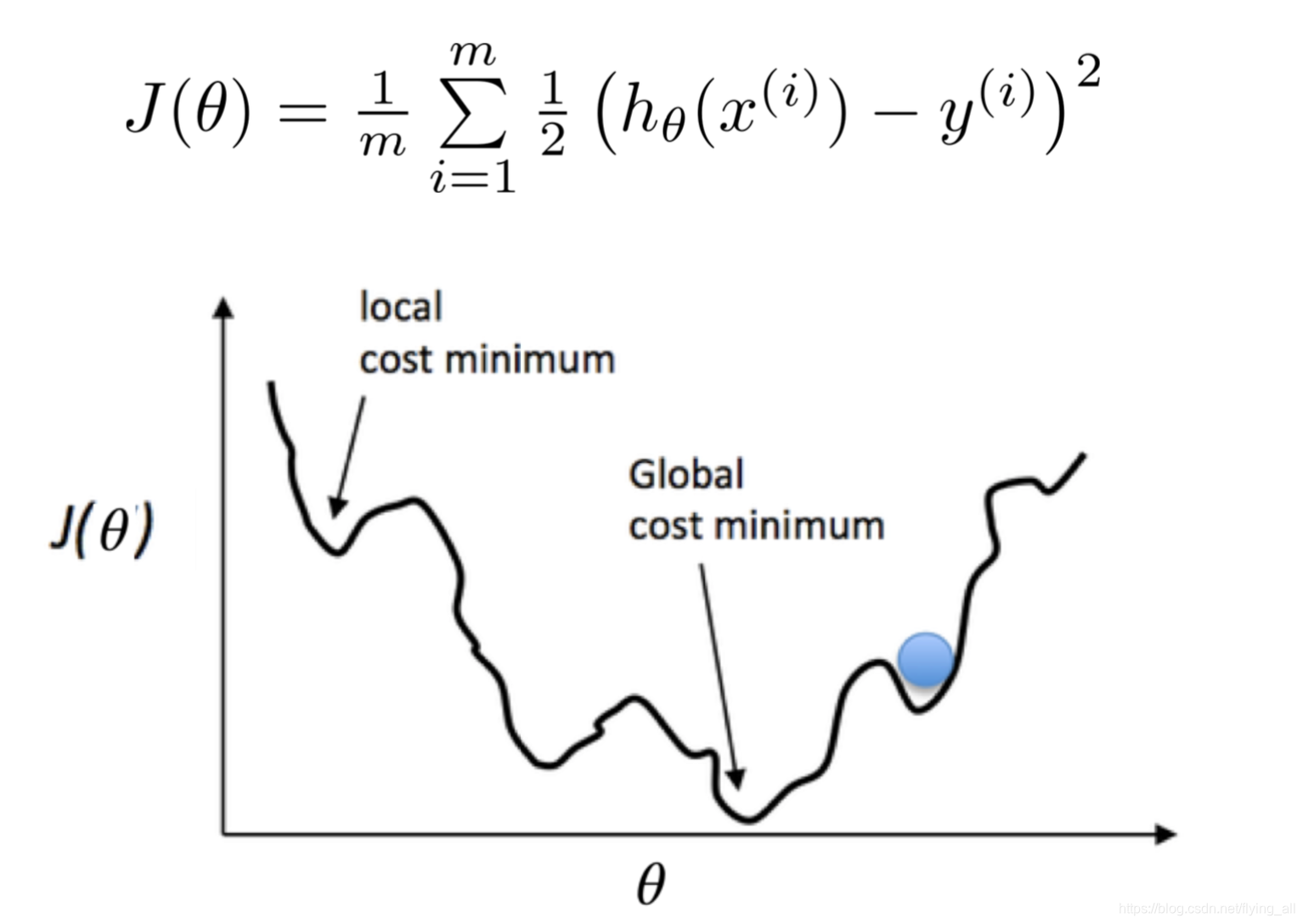
因为 h θ ( x ) h_\theta(x) hθ(x)表示的是概率。对于正样本(y=1)来说, h θ ( x ) h_\theta(x) hθ(x)越大越好,那么 l o g ( h θ ( x ) ) log(h_\theta(x)) log(hθ(x)),越大越好,推理出 − l o g ( h θ ( x ) ) -log(h_\theta(x)) −log(hθ(x)),越小越好。
对于负样本(y=0)来说, h θ ( x ) h_\theta(x) hθ(x)越小越好,所以那么 1 − h θ ( x ) 1-h_\theta(x) 1−hθ(x)越大越好, l o g ( 1 − h θ ( x ) ) log(1-h_\theta(x)) log(1−hθ(x)),越大越好,推理出 − l o g ( 1 − h θ ( x ) ) -log(1-h_\theta(x)) −log(1−hθ(x)),越小越好。
加log函数是因为在计算损失函数的时候多个样本的损失会相乘,概率相乘在大数据量下会发生溢出。加上log,将乘法改为加法,解决溢出问题。
所以得到损失函数为:
C o s t ( h θ ( x ) , y ) = − l o g ( h θ ( x ) ) Cost(h_\theta(x),y)=-log(h_\theta(x)) Cost(hθ(x),y)=−log(hθ(x)), if y=1
C o s t ( h θ ( x ) , y ) = − l o g ( 1 − h θ ( x ) ) Cost(h_\theta(x),y)=-log(1-h_\theta(x)) Cost(hθ(x),y)=−log(1−hθ(x)), if y=0
最后的数学公式:
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(\theta)=-\dfrac{1}{m}[\sum_{i=1}^my^{(i)}log(h_\theta(x^{(i)})) +(1-y^{(i)})log(1-h_\theta(x^{(i)}))] J(θ)=−m1[∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
加上正则化项之后变为:
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\dfrac{1}{m}[\sum_{i=1}^my^{(i)}log(h_\theta(x^{(i)})) +(1-y^{(i)})log(1-h_\theta(x^{(i)}))]+\dfrac{\lambda}{2m}\sum_{j=1}^n\theta_j^2 J(θ)=−m1[∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+2mλ∑j=1nθj2
解决损失韩式同样用梯度下降
4.5 多分类问题
上面谈到的是二分类。在解决多分类问题的时候可以采用 one vs one 和 one vs rest两种方法。
5 混淆矩阵评判标准
参考链接混淆矩阵评价指标_一文搞懂分类算法中常用的评估指标。