在机器学习中,误差被定义为学习器的实际预测输出与样本真实输出之间的差异。
误差可以进一步分为训练误差和测试误差两类。训练误差指的是学习器在训练数据集上的误差,也称经验误差;测试误差指的是学习器在新样本上的误差,也称泛化误差。
训练误差描述的是输入属性与输出分类之间的相关性,能够判定给定的问题是不是一个容易学习的问题。测试误差则反映了学习器对未知的测试数据集的预测能力,是机器学习中的重要概念。实用的学习器都是测试误差较低,即在新样本上表现较好的学习器。
学习器依赖已知数据对真实情况进行拟合,即由学习器得到的模型要尽可能逼近真实模型,因此要在训练数据集中尽可能提取出适用于所有未知数据的普适规律。
然而,一旦过于看重训练误差,一味追求预测规律与训练数据的符合程度,就会把训练样本自身的一些非普适特性误认为所有数据的普遍性质,从而导致学习器泛化能力的下降。这就是过拟合现象,把训练数据的特征错当做整体的特征。
泛化误差的构成可以分为三部分:偏差(bias)、方差(variance)和噪声(noise)。
偏差表示算法预测值和真实结果之间的偏离程度,刻画的是模型的欠拟合特性;方差表示数据的扰动对预测性能的影响,刻画的是模型的过拟合特性;噪声表示在当前学习任务上能够达到的最小泛化误差,刻画的是任务本身的难度。对任何实际的模型来说,偏差和方差都难以实现同时优化,反映出欠拟合与过拟合之间难以调和的矛盾。
噪声也叫作不可约误差(irreducible error),体现的是待学习问题本身的难度,并不能通过模型的训练加以改善。噪声来源于数据自身的不确定性,如果按照 y = x + ϵ , ϵ ∈ N ( 0 , σ 2 ) y=x+ϵ,ϵ\in N(0,σ^2) y=x+ϵ,ϵ∈N(0,σ2) 生成数据,并对生成的数据进行线性拟合的话,高斯噪声的方差 σ 2 σ^2 σ2 就属于不可约误差。噪声的方差 σ 2 σ^2 σ2 越大,线性拟合的难度也就越高。
除了噪声之外,偏差和方差都与模型本身有关,两者对误差的影响可以用误差的偏差 - 方差分解(bias-variance decomposition)来表示。偏差的含义是模型预测值的期望和真实结果之间的区别,如果偏差为 0,模型给出的估计的就是无偏估计。但这个概念是统计意义上的概念,它并不意味着每个预测值都与真实值吻合。方差的含义则是模型预测值的方差,也就是预测值本身的波动程度,方差越小意味着模型越有效。抛开噪声不论,模型的误差就等于偏差的平方与方差之和。
E ( y 0 − f ^ ( x 0 ) ) 2 = V a r ( f ^ ( x 0 ) ) + [ B i a s ( f ^ ( x 0 ) ) ] 2 + V a r ( ε ) E\left ( y_0-\hat{f}\left ( x_0 \right ) \right ) ^2=Var\left ( \hat{f} \left ( x_0 \right ) \right )+\left [ Bias\left ( \hat{f} \left ( x_0 \right ) \right ) \right ]^2+Var\left ( \varepsilon \right ) E(y0−f^(x0))2=Var(f^(x0))+[Bias(f^(x0))]2+Var(ε)
偏差和方差之间的折中与模型自身的特性息息相关。偏差来源于模型中的错误假设,偏差过高就意味着模型所代表的特征和分类结果之间的关系是错误的,对应着欠拟合现象;方差则来源于模型对训练数据波动的过度敏感,方差过高意味着模型对数据中的随机噪声也进行了建模,将本不属于特征 - 分类关系中的随机特性也纳入到模型之中,对应着过拟合现象。
理想的模型应该是低偏差低方差的双低模型,一般来说,模型的复杂度越低,其偏差也就越高;模型的复杂度越高,其方差也就越高。到最小值。这样的模型既能提取出特征和分类结果之间的关系,又不至于放大噪声和干扰的影响。
解决过拟合问题,常见的做法是正则化,即添加额外的惩罚项。
C p = 1 N ( R S S + 2 d σ ^ 2 ) C_p=\frac{1}{N} \left ( RSS+2d\hat{\sigma}^2\right ) Cp=N1(RSS+2dσ^2)
其中 d d d为模型特征个数,
R S S = ∑ i = 1 N ( y i − f ^ ( x i ) ) 2 RSS=\sum_{i=1}^{N}\left ( y_i-\hat{f}\left ( x_i \right ) \right )^2 RSS=i=1∑N(yi−f^(xi))2
σ ^ 2 \hat{\sigma}^2 σ^2为模型预测误差的方差的估计值,即残差的方差。
AIC赤池信息量准则:
A I C = 1 d σ ^ 2 ( R S S + 2 d σ ^ 2 ) AIC=\frac{1}{d\hat{\sigma}^2 } \left ( RSS+2d\hat{\sigma}^2 \right ) AIC=dσ^21(RSS+2dσ^2)
BIC贝叶斯信息量准则:
B I C = 1 n ( R S S + log ( n ) d σ ^ 2 ) BIC=\frac{1}{n} \left ( RSS+\log_{}{\left ( n \right ) } d\hat{ \sigma}^2 \right ) BIC=n1(RSS+log(n)dσ^2)
k 折交叉验证将原始数据集随机划分为 k 个相同大小的子集,并进行 k 轮验证。每一轮验证都选择一个子集作为验证集,而将剩余的 k−1 个子样本用作训练集。由于每一轮中选择的验证集都互不相同,每一轮验证得到的结果也是不同的,k 个结果的均值就是对泛化性能的最终估计值。
做特征选择的目标就是:从p个特征中选择m个特征,使得对应的模型的测试误差的估计最小。对应的方法有:
- 最优子集选择:
(i) 记不含任何特征的模型为 M 0 M_0 M0,计算这个 M 0 M_0 M0的测试误差。
(ii) 在 M 0 M_0 M0基础上增加一个变量,计算p个模型的RSS,选择RSS最小的模型记作 M 1 M_1 M1,并计算该模型 M 1 M_1 M1的测试误差。
(iii) 再增加变量,计算p-1个模型的RSS,并选择RSS最小的模型记作 M 2 M_2 M2 ,并计算该模型的测试误差。
(iv) 重复以上过程直到拟合的模型有p个特征为止,并选择p+1个模型 { M 0 , M 1 , … M p } \left \{ M_0,M_1,\dots M_p\right \} {
M0,M1,…Mp}中测试误差最小的模型作为最优模型。
- 向前逐步选择:
最优子集选择虽然在原理上很直观,但是随着数据特征维度p的增加,子集的数量为 2 p 2^p 2p ,计算效率非常低下且需要的计算内存也很高,在大数据的背景下显然不适用。因此,我们需要把最优子集选择的运算效率提高,因此向前逐步选择算法的过程如下:
(i) 记不含任何特征的模型为 M 0 M_0 M0,计算这个 M 0 M_0 M0的测试误差。
(ii) 在 M 0 M_0 M0基础上增加一个变量,计算p个模型的RSS,选择RSS最小的模型记作 M 1 M_1 M1 ,并计算该模型 M 1 M_1 M1 的测试误差。
(iii) 在最小的RSS模型下继续增加一个变量,选择RSS最小的模型记作 M 2 M_2 M2,并计算该模型 M 2 M_2 M2的测试误差。
(iv) 以此类推,重复以上过程直到拟合的模型有p个特征为止,并选择p+1个模型 { M 0 , M 1 , … M p } \left \{ M_0,M_1,\dots M_p\right \} {
M0,M1,…Mp}中测试误差最小的模型作为最优模型。
在线性回归里,最常见的正则化方式就是在损失函数(loss function)中添加正则化项(regularizer),而添加的正则化项 R ( λ ) R(λ) R(λ)往往是待估计参数的 p − p- p− 范数。将均方误差和参数的范数之和作为一个整体来进行约束优化,相当于额外添加了一重关于参数的限制条件,避免大量参数同时出现较大的取值。由于正则化的作用通常是让参数估计值的幅度下降,因此在统计学中它也被称为系数收缩方法(shrinkage method)。
将正则化项应用在基于最小二乘法的线性回归中,就可以得到线性回归的不同修正(penalized linear regression)。添加正则化项之后的损失函数可以写成拉格朗日乘子的形式
J ( w ) = ∑ i = 1 N ( y i − w 0 − ∑ j = 1 P w j x i j ) 2 + λ ∑ j = 1 P ∥ w ∥ p J\left ( w \right ) = \sum_{i = 1}^{N} \left ( y_i-w_0-\sum_{j = 1}^{P}w_jx_{ij} \right )^2+\lambda\sum_{j = 1}^{P}\left \| w \right \|_p J(w)=i=1∑N(yi−w0−j=1∑Pwjxij)2+λj=1∑P∥w∥p
其中的 λ λ λ 是用来平衡均方误差和参数约束的超参数。当正则化项为 1- 范数时,修正结果就是 LASSO;当正则化项为 2- 范数的平方时,修正结果就是岭回归;当正则化项是 1- 范数和 2- 范数平方的线性组合 α ∣ ∣ w ∣ ∣ 2 + ( 1 − α ) ∣ ∣ w ∣ ∣ 1 α∣∣w∣∣_2+(1−α)∣∣w∣∣_1 α∣∣w∣∣2+(1−α)∣∣w∣∣1 时,修正结果就是弹性网络(elastic net)。
主成分分析是一种主要的降维方法,它利用正交变换将一组可能存在相关性的变量转换成一组线性无关的变量,这些线性无关的变量就是主成分。
主成分分析遵循如下的步骤:
数据规范化:对 m 个样本的相同属性值求出算术平均数,再用原始数据减去平均数,得到规范化后的数据;
协方差矩阵计算:对规范化后的新样本计算不同属性之间的协方差矩阵,如果每个样本有 n 个属性,得到的协方差矩阵就是 n 维方阵;
特征值分解:求解协方差矩阵的特征值和特征向量,并将特征向量归一化为单位向量;
降维处理:将特征值按照降序排序,保留其中最大的 k 个,再将其对应的 k 个特征向量分别作为列向量组成特征向量矩阵;
数据投影:将减去均值后的 m×n 维数据矩阵和由 k 个特征向量组成的 n×k 维特征向量矩阵相乘,得到的 m×k 维矩阵就是原始数据的投影。
经过这几步简单的数学运算后,原始的 n 维特征就被映射到新的 k 维特征之上。这些相互正交的新特征就是主成分。需要注意的是,主成分分析中降维的实现并不是简单地在原始特征中选择一些保留,而是利用原始特征之间的相关性重新构造出新的特征。
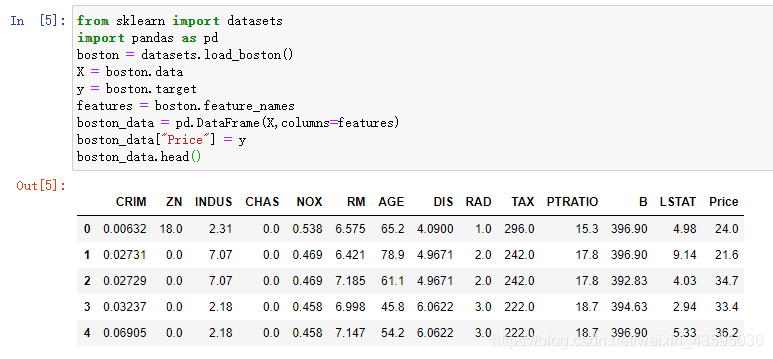
特征提取的实例:向前逐步回归
案例来源:https://blog.csdn.net/weixin_44835596/article/details/89763300
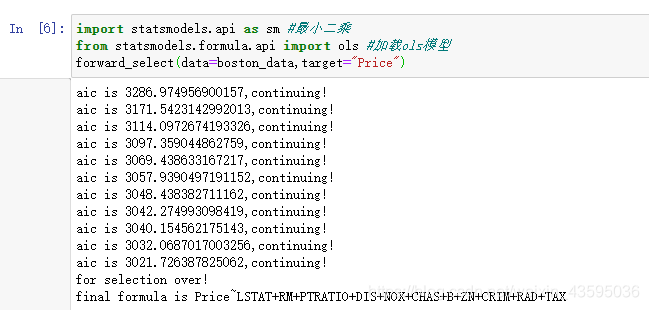
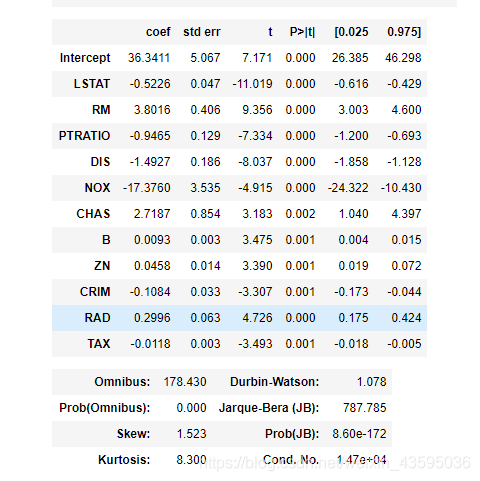
根据AIC准则定义向前逐步回归进行变量筛选


岭回归实例分享:
sklearn.linear_model.ridge_regression(X, y, alpha, *, sample_weight=None, solver=‘auto’,
max_iter=None, tol=0.001, verbose=0, random_state=None, return_n_iter=False,
return_intercept=False, check_input=True)

Lasso实例分享:
class sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, normalize=False,
precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False,
random_state=None, selection=‘cyclic’)

感谢Datawhale团队为开源学习做出的贡献!
参考文献:
https://github.com/datawhalechina/team-learning-data-mining/tree/master/EnsembleLearning