KCF

前三section不是核心

4 BUILDING BLOCKS

4.1 Linear Regression

给出岭回归的目标函数和解的形式：
在这里插入图片描述

上标H表示Hermitian transpose，是考虑了复数的转置，如果X为实矩阵，则对应的就是转置

4.2 Cyclic Shifts

介绍循环移位，对于一个向量x，乘以一个permutation matrix，起到交换x中元素位置的作用。permutation matrix定义如下：
在这里插入图片描述
对1维向量的可视化表示如下：

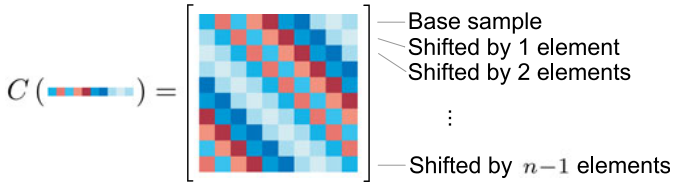
对2维图片的表示如下：

可以看到，这个操作大致就是做平移。
可以对信号做多次平移，然后把所有的平移信号表示成为一个矩阵

注意：这种平移会产生失真，例如[1,2,3,4]平移一次变为[2,3,4,1]，这其实造成了边缘的扭曲。补救办法如下。做padding，[1,2,3,4]先padding为[0,0,0,1,2,3,4,0,0,0]，然后平移为[0,0,1,2,3,4,0,0,0,0]

4.3 Circulant Matrices

对x进行平移，就得到了循环矩阵，矩阵记为X，基于x构建循环矩阵的操作记为C(x)：
在这里插入图片描述
循环矩阵有个性质，对循环矩阵X，可以表示为一个对角形式：

其中F是固定的，被称为DFT matrix，与x无关， $\hat{x}$ 表示对x求离散傅里叶变换（DFT）

4.4 Putting It All Together

那么有了上述性质，如果将循环矩阵作为岭回归训练的输入，那么闭式解也可以用DFT表示：
在这里插入图片描述
其中，圆圈内加点这个操作表示element product，两个向量做元素积。

5 NON-LINEAR REGRESSION

那么，可不可以做岭回归的时候不用X，而是用它的一种非线性变换之后的特征呢？这就引入了核函数。

5.1 Kernel Trick – Brief Overview

核函数的几个特征如下：

1）闭式解w是是用核函数表示的，但要训练的变量变成了 $\alpha$ ：
在这里插入图片描述
2） $\phi(x)$ 是隐式的非线性变换函数，其出现形式均与其转置相关联，也就是表示成了核函数：

3）对于所有的训练样本，可以都将其信息储存在一个核矩阵K中，K的表达形式如下：

4）对于新给出一个特征z，要求其回归值，使用以下公式：
在这里插入图片描述

5.2 Fast Kernel Regression

虽然5.1中给出了w的闭式解，但 $\alpha$ 怎么求也没说，相当于在回归过程中把要训练的权重从w变成了 $\alpha$ ，因为在5.1的4）中可以看到，回归以下新的z，需要的就是 $\alpha$ 。 $\alpha$ 的闭式解如下：
在这里插入图片描述
这种计算速度还是慢，因为要求逆。当训练数据很大的话，求解很慢。所以可不可以也对角化？

Theorem 1给出，对于高斯核，多项式核函数等一些常见的函数，如果X为循环矩阵，那么由其构造的核矩阵仍然是循环矩阵。那么 $\alpha$ 的闭式解就变成了：
在这里插入图片描述
其中 $\hat{k}^{xx}$ 这一项是：

注意：上述的意思是有了x，就可以构造X，就可构造K，可以反算 $\alpha$ ，但很慢。有了x，有了核函数，如果X是循环矩阵，那么就直接可以算 $\hat{k}^{xx}$ ，然后就可以直接算 $\hat{\alpha}$ ，然后就可以通过逆DFT算 $\alpha$ 。