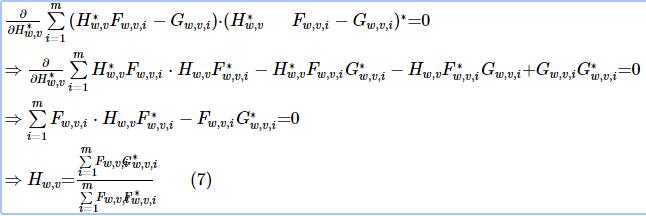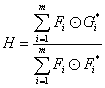转载——correlation filter tracking，

Correlation Filter Object Tracking入门简介

近期一直在研究相关滤波（Correlation filter）的东西，自己没啥地方记录的，本子也破的不行了，就这随便记录一下自己的感想，供以后回忆用！~这篇文章主要是讲一下最早应用的文章Minimum Output Sum of Squared Error(MOSSE)当中的一些思想和自己的一些基本理解。

一、基础概念

维基百科中关于相关的定义： 
在概率论和统计学中，相关（Correlation，或称相关系数或关联系数），显示两个随机变量之间线性关系的强度和方向。在统计学中，相关的意义是用来衡量两个变量相对于其相互独立的距离。在这个广义的定义下，有许多根据数据特点而定义的用来衡量数据相关的系数。

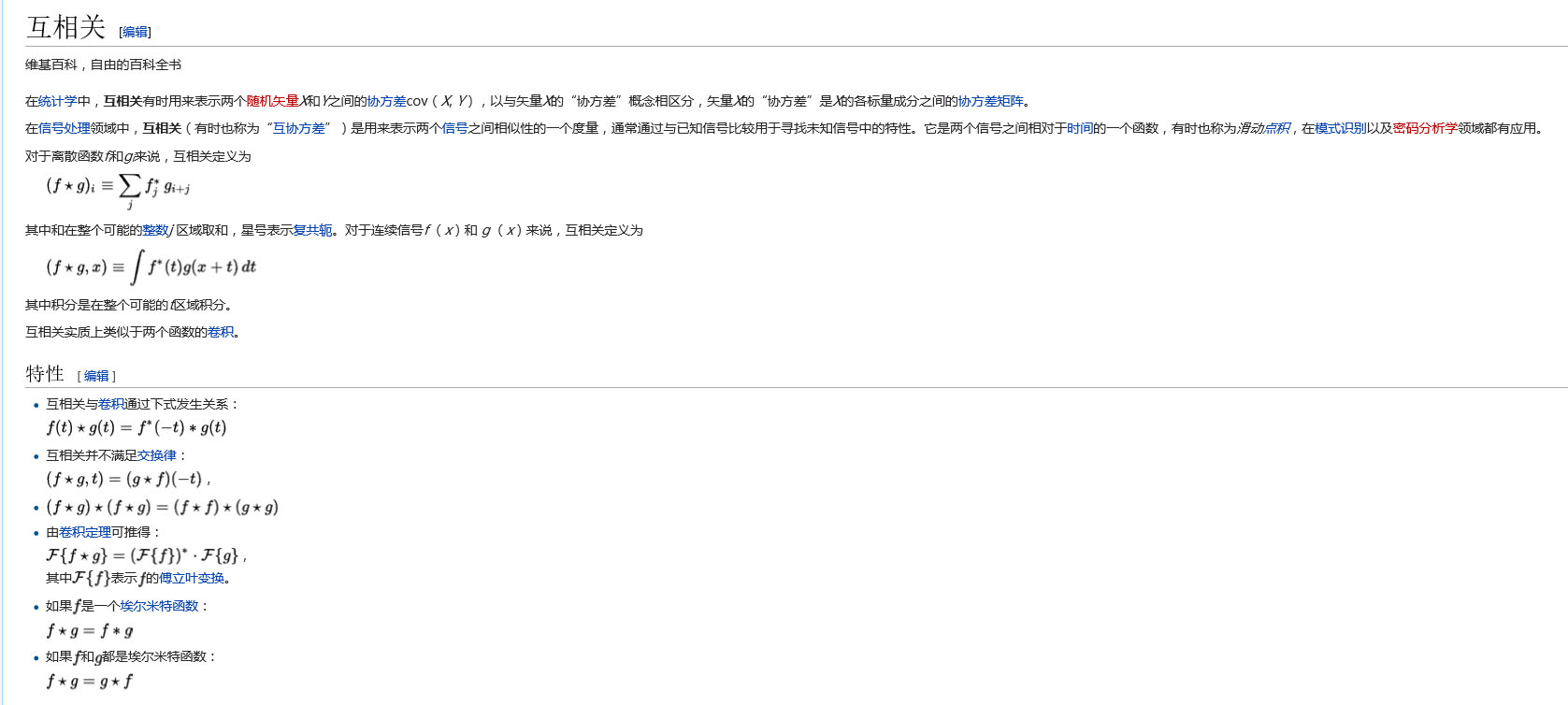
相关(correlation)的直观解释就是衡量两个函数在某个时刻的相似的程度。

相关又分为自相关（auto-correlation）和互相关（cross-correlation）。 
互相关的概念： 

基础的概念大概就这么些吧，其他的想要了解的可以自己多查一下资料，就是先对这些有一个概念。

二、相关在tracking中的应用

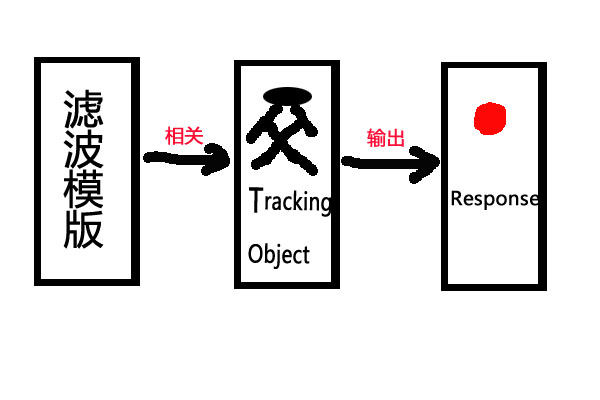
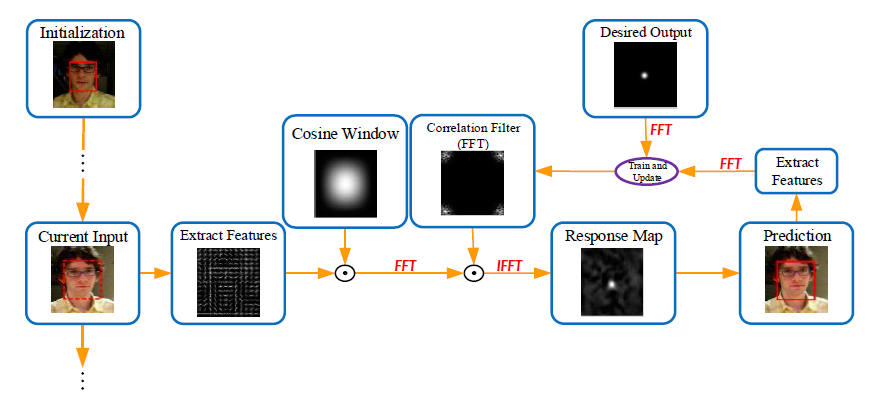
相关（correlation filter）应用在tracking方面的最为直观的方法：相关就是衡量两个信号相似值得度量。如果两个信号相似越高，就表明这两个信号的相关值就越大。在tracking的应用当中，我们的目的就是设计这么一个模版，使得当模版和输入的图片目标做相关时，能在目标的中心位置得到最大的响应值。如下图所示：

第一步：

寻找一个滤波模板，使得它在目标上的响应值最大，写成公式就是： 
g=h★f—————————————-① 
g表示响应输出值 
h表示滤波模板 
f表示输入图像

g可以使任意形式的响应输出，大多数情况下为gaussian形状。明显可以看出，在公式当中，只有h是未知的，即滤波模板，这就是我们所要去计算的，所要得到的。从公式来看，这个并不是很复杂，但是相关滤波的方法在tracking当中的速度为什么这么快呢？这个就要归功于傅里叶变换。在所有的求解过程当中都是用到了快速傅里叶变换FFT。由卷积定理的correlation版本可以知道，函数互相关傅里叶变换等于函数傅里叶变换的乘积。如公式②所示。 
F(h)★f=（F(h)）*⊙F(f)——————–②

其中F（·）表示傅里叶变换，⊙表示点乘，接下来，假设输入图片f所含的像素的个数为n，而已知FFT变换的时间复杂度为O(nlogn),由此可知，②式的时间复杂度也为O(nlogn)。

第二步：

明白了上面所说的一些观点之后也就比较好理解了，也就可以明白为什么相关滤波类型的tracking algorithm的计算时间比较快，也就是想要表达的主要的内容。本步主要说一下怎么求h。

为了看着方便，我们设 F=F(f),(F(h))* = H*,F(g)=G.由此可以得到 
H*=G/F————————————–③

这里我们的目标图像只有一张的时候，但是在实际使用的过程当中，目标会由于外观、光照等因素的改变发生变换，我们需要同时考虑目标不同状态下的情况，则以不同状态下的m个图像作为参考，以此计算得到的模板提高滤波模板的鲁棒性，则有： 
———————④

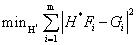
求解出来等式④并不算困难，根据卷积定理，在频率域的计算都是元素为单位的，因此可以分别求出来H*当中的每一个元素，就可以得出： 
—————⑤ 
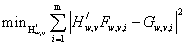
接下来就是熟悉的求导，使导数等于零。解出来就可以了。

但是在MOSSE论文当中提到了，复数域求导和实数域的求导是不一样的： 

按照上述的方法把得到的H进行处理，得到： 

这就是我们最终求得的滤波模板，也就是我们所要求得核心东西。 
接下来就可以开始跟踪了。在跟踪的过程中，我们只需要把以上模板与当前帧的图像作相关操作，将得到的响应结果中最大的那点对应坐标作为目标在当前帧位置就可以了（相当于在2维上平移我们的模板）。然后，模板的更新方式可以按照如下的方式进行： 
H(t)=(1−η)H(t−1)+ηH(t)——————–⑥ 
H(t)表示当前帧模板，H(t-1)表示前一阵模板，η为学习率。

总结

总得来说，MOSSE方法开创了CF在tracking方面的先河，而在后面的一系列文章里，我们将介绍一系列用概率论、岭回归等理论对其作进一步提升的文章。特别是我研究的最多的KCF方向的文章，我会进行详细的分析和介绍。

Correlation Filter-based Tracking Frame

Discriminative Correlation Filter（DCF），即判别相关滤波器，是Visual Tracking领域应用最为广泛的跟踪算法。其核心思想是：由于每一帧中被良好检测的目标都提供了描述该目标的信息，因此完全可以通过用每一帧中的目标区域作为训练样本来进行模型的训练，具体做法是通过已经跟踪的若干帧中目标的位置，提取出我们关心的特征，训练出一个滤波器模板，对于新帧中可能的目标区域，提取出该区域特征，与滤波器模板作相关，根据相关值得到在新帧中目标的预测位置，并在以该位置为中心提取出特征，反过来进一步训练滤波器模型，并重复上述步骤进行后续的目标跟踪与模型训练。通过这种方法，就实现了模型的在线训练与目标的实时跟踪。 

Adaptive Correlation Filters

Minimum Output Sum of Squared Error (MOSSE)

Minimum Output Sum of Squared Error (MOSSE) developed by Bolme et al.的提出极大地改善了相关滤波器跟踪算法的performance，在提升精度的同时降低了求解的复杂度。

t个目标区域样本分别为 f1,f2,⋯,ft ，通过滤波器 ht ，期望输出 gi （通常为二维高斯函数，峰值位于目标区域中心），最小化均方误差： 

ε=∑j=1t||ht⋆fj−gi||2=1MN∑j=1t||H⎯⎯⎯tFj−Gj||2

对 Ht 求导，令导数为0，得： 

Ht=∑tj=1G⎯⎯⎯jFj∑tj=1F⎯⎯⎯jFj

对于t+1帧，假设其在第t帧的目标区域内提取得到特征图z，那么计算 ht 与z的相关值 

y=−1{H⎯⎯⎯tZ}

y的最大值的位置即被认为是t+1帧中目标区域的中心点.

我们保持目标区域尺寸不变，将其中心点进行移动相应位置，就得到了在新帧中的目标区域。对该区域进行特征提取，然后加入到训练集中对模型进行更新得到 ht+1 后，即可进行下一帧 
中的目标检测了。 

在实际的tracking过程中，一般使用如下方法来更新模型: 

A1B1AtBtHt=====G⎯⎯⎯1F1F⎯⎯⎯1F1(1−η)At−1+ηG⎯⎯⎯tFt(1−η)Bt−1+ηF⎯⎯⎯tFtAtBt

其中 η 为学习率。 

缺点

• 只使用了灰度作为特征，模型所使用的特征维数太低，难以很好地反映目标的特性。
• 只估算了目标区域中心点在帧间的平移运动，而没有考虑目标在运动过程中反映在画面上的尺度变化，在目标尺度发生改变时难以适应。

Discriminative Scale Space Tracking Filter (DSST)

对MOSSE的改进：

• 使用fHoG替代灰度（通常fHoG为31dims，而DSST实际使用28dims）
• 考虑目标尺度变化 
  
  

不考虑尺度变化 
只考虑单个目标，设特征维数为d，则特征图可记作 fl,l=1,2,⋯,d 。滤波器应和特征图匹配，误差函数： 

ε=||∑l=1dhl⋆fl−g||2+λ∑l=1d||hl||2

引入 λ 项是为了控制滤波器频域参数求解过程中的避免除0，另一方面也可以控制滤波器参数变化范围， λ 越小，滤波器参数变化范围越大。

对上式做傅里叶变换，求导，令导数为0，得： 

Hl=G⎯⎯⎯Fl∑dk=1Fk⎯⎯⎯⎯⎯Fk+λ

在实际操作中，可以用下式更新模型： 

AltBtHlt===(1−η)Alt−1+ηG⎯⎯⎯tFlt(1−η)Bt−1+η∑k=1dFkt⎯⎯⎯⎯⎯FktAltBt+λ

新帧预测： 

y=−1{∑dl=1Alt⎯⎯⎯⎯ZlBt+λ}

考虑尺度变化 
滤波器和特征图由 d×M×N 改为 d×M×N×S ，S = num of scales，即构造金字塔。这导致复杂度增大为 O(dMNS×logMNS) 。 

改进思路，两组滤波器模板：

• d个大小为 M×N 的二维位置滤波器
• d×M×N 个大小为S的一维尺度滤波器

位置滤波器的训练方法同前，而尺度滤波器则是在确定了目标区域中心后，对于尺度因子s，提取出其对应区域的d个 M×N 的二维矩阵后，将其拉成一条向量，作为尺度因子s下的 d×M×N 维特征，构成尺度滤波器。 

完整算法

• 估算位置 
  
  • 在帧 It 中根据前一帧的位置 pt−1  和尺度因子 st−1 划定区域提取特征 zlocat
  • 在 zlocat 与位置滤波器 Alocat−1,Blocat−1 做相关得到 ylocat
  • 将 ylocat 最大值点设为当前帧的目标中心 pt
• 估算尺度 
  
  • 在帧 It 中根据位置 pt 和前一帧的尺度因子 st−1 划定区域，缩放后得到S个区域，提取特征 zscalet
  • 将征 zscalet 与尺度滤波器 Ascalet−1,Bscalet−1 做相关得到 yscalet
  • 将 yscalet 最大值点设为当前帧的目标尺度 st
• 更新模型 
  
  • 在帧 It 中根据估算出的位置 pt 和尺度 st 划定区域提取特征，得到 flocat 和 fscalet
  • 更新位置滤波器得到 Alocat,Blocat
  • 更新尺度滤波器得到 Ascalet,Bscalet

复杂度 O(dMN×logMN+dMNS×logS)  

缺点

• 难以适应大幅度形变、遮挡等
• 循环卷积边缘效应 
   
  SRDCF对此做出了改进。

Kernelized Correlation Filters

The overall performance may be limited because the MOSSE filters can be viewed as simple linear classifiers. By taking advantage of kernel trick, correlation filters are supposed to be more powerful.

Building Blocks

Linear Regression

考虑： 

minw∑t(f(xi)−yi)2+λ⋅||w||2

λ 是一个控制过拟合的参数，则 w 的解为： 

w=(XTX+λI)−1XTy

在复数域中，上是中的转置（T）替换为共轭转置（H）。

Circulant Matrices

仅考虑一维单通道信号 x 的情形，二维可以类推。 x 的轮换矩阵为： 

X=C(x)=⎡⎣⎢⎢⎢⎢⎢⎢x1xnxn−1⋮x2x2x1xn⋮x3x3x2x1⋮x4⋯⋯⋯⋱⋯xnxn−1xn−2⋮x1⎤⎦⎥⎥⎥⎥⎥⎥

轮换矩阵 X 有一个重要性质： 

X=F diag(x̂ ) FH

其中 F 是DFT矩阵（constant）， x̂ =(x) 。

Putting it all together

考虑 XHX ： 

XHX==F diag(x̂ ∗) FHFdiag(x̂ )FHF diag(x̂ ∗) diag(x̂ ) FH

定义 ⊙ 为element-wise product，则上式可表示为： 

XHX=F diag(x̂ ∗⊙x̂ ) FH

Linear regression的解的傅里叶变换可以表示为： 

ŵ =diag(x̂ ∗x̂ ∗⊙x̂ +λ)ŷ =x̂ ∗⊙ŷ x̂ ∗⊙x̂ +λ

Non-linear Regression

Kernel Trick

将线性问题转换为 ϕ(x) 空间中的非线性问题可以使用核函数，即：

• 将解 w 表示为 ϕ(x) 的线性组合： 
  
  w=∑iαiϕ(xi)
  
  求解 w 的过程变为对偶空间（Dual Space）中求解 α 的过程。
• 将点积表示为： 
  
  ϕT(x)ϕ(x′)=κ(x,x′)

核函数不需要给出高维空间中的向量的具体表达式，就可以实现从低维到高维的映射。

Fast Kernel Regression

核函数回归在对偶空间的理论解： 

α=(K+λI)−1y

其中 Ki,j=κ(xi,xj) 。 

定理：Kernel Matrix  K 轮回的条件

给定轮换矩阵 C(x) ，如果核函数对任意的置换阵 M 均满足 κ(x,x′)=κ(Mx,Mx′) ，那么相应的核矩阵 K 也是轮回的。 

满足上述定理的核函数有：

• Ridial Basis Function kernels - e.g., Gaussian.
• Dot-product kernels - e.g., linear, polynomial.
• Additive kernels - e.g., intersection,  χ2  and Hellinger kernels.
• Exponentiated additive kernels.

这时可以将 α 在频域的解表示为： 

α̂ =ŷ k̂ xx+λ

其中 kxx 是kernel matrix  K=C(kxx) 的第一行，其物理意义是 

kxx′i=κ(x′,Pi−1x)

的傅里叶变换。

Fast Detection

我们希望评估的image patch为 z ，则kernel matirx： 

Kz=C(kxz)

其中 kxz 是 x, z 的kernel correlation。 
回归函数： 

f(z)=(Kz)Tα

它等价于： 

f̂ (z)=k̂ xz⊙α̂ 

Fast Kernel Correlation

Radial Basis Function and Gaussian Kernels

RBF kernels通常具有下列形式： 

kxx′i=κ(x′,Pi−1x)=h(||x′−Pi−1x||2)=h(||x||2+||x′||2−2x′TPi−1x)

由于置换阵不影响 x 的模，因此可以写成： 

kxx′=h(||x||2+||x′||2−2−1(x̂ ∗⊙x̂ ′))

特别地，高斯核： 

kxx′=exp(−1σ2(||x||2+||x′||2−2−1(x̂ ∗⊙x̂ ′)))

Dot-product and Polynomial Kernels

To be continued.

Multiple Channels

A dotproduct can be computed by simply summing the individual dot-products for each channel. By linearity of the DFT, this allows us to sum the result for each channel in the Fourier domain.

以高斯核为例： 

kxx′=exp(−1σ2(||x||2+||x′||2−2−1(∑cx̂ ∗c⊙x̂ ′c)))

Algorithms

实际使用中，Tracking模板的更新可以用学习率控制，参考Danelljan, Martin, et al. “Adaptive color attributes for real-time visual tracking.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2014. 

αp=∑pj=1βjŷ jû jx∑pj=1βjû jx(û jx+λ)

分子和分母 αp=ApNApD 分别按下述策略更新： 

ApNApDx̂ p===(1−γ)Ap−1N+γŷ pû px(1−γ)Ap−1D+γû px(û px+λ)(1−γ)x̂ p−1+γx̂ p

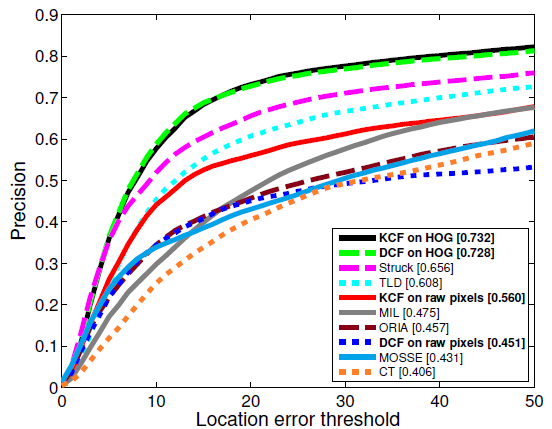
Experiments

Benchmark: Y. Wu, J. Lim, and M. H. Yang, “Online object tracking: A benchmark,” in CVPR, 2013.

• KCF=Gaussian Kernel
• DCF=Linear Kernel

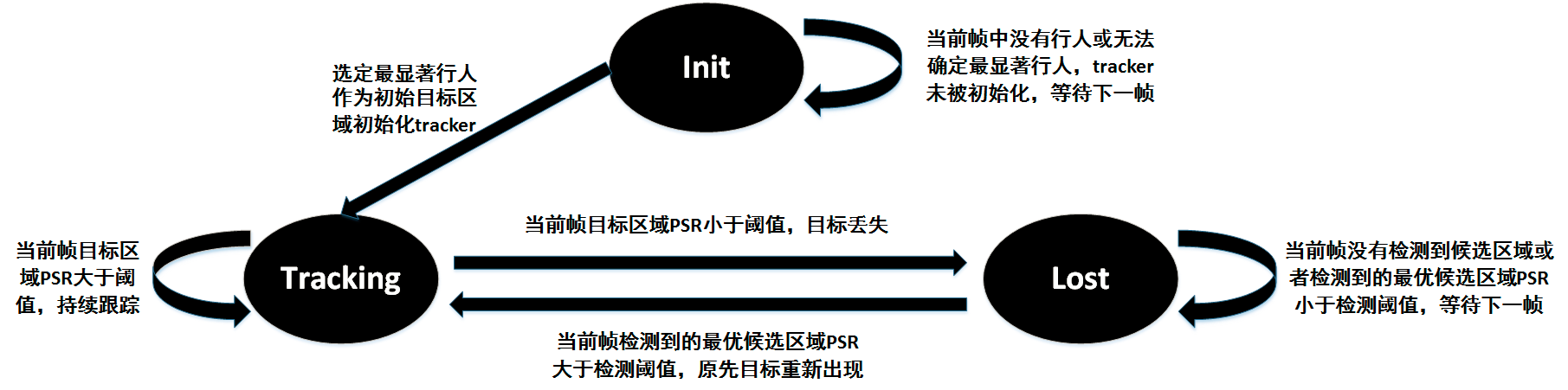
Detection-Tracking System

The Combinition of Detection & Tracking

Target Lost

定义：Peak to Sidelobe Ratio (PSR)

设滤波器模板与目标区域特征作相关后得到响应为G，其最大值为 Gmax ，以 Gmax 的位置中心 11×11 的区域内响应平均值为 μ ，方差为 σ2 ，则 PSR=Gmax−μσ2 。

一般而言，当目标区域和模型较为相符时， PSR>20 ；而 PSR<10 时基本可以认为目标已经丢失。

问题：

仍然缺少自动学习 PSR 阈值的相关算法。

Re-detection

当目标丢失、重新detect时，对于得到的所有候选区域，用原先的tracking模板与候选区域逐个作相关，取响应值最大值最大的候选区域，若候选区域的PSR大于跟踪时的PSR阈值，则可以认为原先跟踪的目标区域已经重新出现。

Anti-deformation

KCF略优于DSST。

问题：

可以通过调整核函数的参数，提高Anti-deformation的能力，但是会造成跟踪到错误的目标，通过Colorname Distance解决？

Scale Estimation

KCF只能实现位置追踪，不能估计尺度变化，目前有两种解决方案：

• 使用DSST Scale Estimator（Danelljan, Martin, et al. “Accurate scale estimation for robust visual tracking.” British Machine Vision Conference, Nottingham, 2014.）。
• 构建一个三层的金字塔，分别是scale变大、不变、变小，和tracking模板做相关，取最大的Response峰值（或PSR）对应的scale。

后者在scale快速变化时会出现斜率过载，但速度快于DSST Scale Estimator （33 scale proposals）。