入门笔记:动态规划之四边形不等式优化(一)

0.前言：

大概大一下学期还是啥时候就听说过这个优化了。现在都大三下了才正式开始学这东西，哈哈，太垮了.这里只记录结论和如何使用。不说证明(也看不懂.

1.使用场合:

优化转移：
1. d p ( i , j ) = m i n { d p ( i , k ) + d p ( k , j ) + w ( i , j ) } dp(i,j)=min\{dp(i,k)+dp(k,j)+w(i,j)\} dp(i,j)=min{ dp(i,k)+dp(k,j)+w(i,j)}
2. d p ( i , j ) = m i n { d p ( i − 1 , k − 1 ) + w ( k , j ) } dp(i,j)=min\{dp(i-1,k-1)+w(k,j)\} dp(i,j)=min{ dp(i−1,k−1)+w(k,j)}

解释:$dp(i,j)$是区间形式且他们存在着一个最优决策点$k$使得$dp(i,j)$取最小值.

第一种转移:石子合并模型
第二种转移:将长度为$n$的序列分成$m$段，求最小值.

2.使用条件:

$w(i,j)$满足 四边形不等式以及单调性 能够推出$dp(i,j)$也满足.

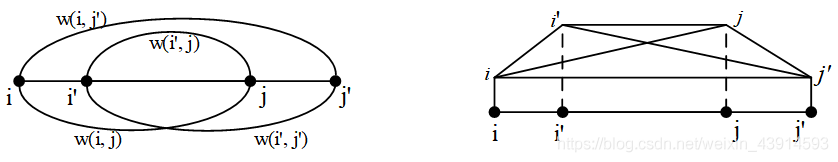
2.1：四边形不等式:两个交错区间的$w$和，小于等于 小区间与大区间的$w$和。

2.2：单调性:小区间的$w$ 小于等于 大区间的$w$.

只要满足这两个条件即可使用。

3.min与max

如果把min改成max,那么使用条件就正好得反过来：

$w(i,j^{\prime })+w(i^{\prime },j)\ge w(i,j)+w(i^{\prime },j^{\prime })$ - 反四边形不等式

$w(i^{\prime },j)\ge w(i,j^{\prime })$ - 单调性：小区间的值大于等于大区间的值

4.优化方法：

用$s(i,j)$记录区间最优决策点,如果$dp(i,j)$满足四边形不等式,则:
$s(i,j-1)\le s(i,j)\le s(i+1,j)$

复杂度降至：$O(n^2)$

5.结论：

其实四边形不等式优化就是二维的决策单调性优化.

一维决策单调性也可以使用四边形不等式优化!

6.例题：

例题一:石子合并（模板）

for (int len = 2 ; len <= m ; len++){
    
    
    for (int i = 1 ; i + len - 1 <= m ; i++){
    
    
        int j = i + len - 1;
        int cost = p[j] - p[i - 1];
        for (int k = s[i][j - 1] ; k <= s[i + 1][j] ; k++){
    
    
            if (dp[i][j] > dp[i][k] + dp[k + 1][j] + cost){
    
    
                dp[i][j] = dp[i][k] + dp[k + 1][j] + cost;
                s[i][j] = k;
            }
        }
    }
}

注意:
① $max$不符合四边形不等式，且可以证明最大值$f(i,j)$的最优决策点一定在区间两端取到.

例题二:[HDU2829] Lawrence

令$dp(i,j)$代表前$i$个数，分成$j$段的最小值.有转移:
d p ( i , j ) = m i n { d p ( k − 1 , j − 1 ) + w ( k , j ) } , k ∈ [ 1 , i ] dp(i,j)=min\{dp(k-1,j-1)+w(k,j)\},k\in[1,i] dp(i,j)=min{ dp(k−1,j−1)+w(k,j)},k∈[1,i]

属于形式$2$.复杂度:$O(n^{2}m)$。展开计算发现其符合四边形不等式以及单调性.优化$k$的枚举即可.

这里注意最优决策点的范围在$[s[i][j-1],s[i+1][j]]$.所以得考虑一个正确的dp顺序和初始化s数组边界:

1.外层顺序枚举$j,2=>m$,内层逆序枚举$i,n=>1$.
2.$s[i][1]=1,s[n+1][i]=n$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pii pair<int,int>
#define pb push_back
#define mp make_pair
#define vi vector<int>
#define vl vector<ll>
const int maxn = 1005 + 5;
const int mod = 1e9 + 7;
ll a[maxn] , dp[maxn][maxn] , p[maxn] , pp[maxn];
int s[maxn][maxn];
ll calc (int l , int r)
{
    
    
    ll g = p[r] - p[l - 1];
    g *= g;
    g -= pp[r] - pp[l - 1];
    g /= 2;
    return g;
}
int main()
{
    
    
    ios::sync_with_stdio(false);
    int n , m;
    while (cin >> n >> m , n && m){
    
    
        m++;
        for (int i = 1 ; i <= n ; i++){
    
    
            cin >> a[i];
            p[i] = p[i - 1] + a[i];
            pp[i] = pp[i - 1] + a[i] * a[i];
        }
        for (int i = 0 ; i <= n ; i++)
            for (int j = 0 ; j <= m ; j++)
                dp[i][j] = 1e15;
        dp[0][0] = 0;
        // 边界
        for (int i = 1 ; i <= n ; i++){
    
    
            dp[i][1] = calc(1 , i);
            s[i][1] = 1;
        }
        // s[i][j-1] <= s[i][j] <= s[i+1][j]
        // 考虑如何安排dp顺序
        for (int j = 2 ; j <= m ; j++){
    
    
            s[n + 1][j] = n;
            for (int i = n ; i >= 1 ; i--){
    
    
                for (int k = s[i][j - 1] ; k <= s[i + 1][j] ; k++){
    
    
                    if (dp[k - 1][j - 1] + calc(k , i) < dp[i][j]){
    
    
                        dp[i][j] = dp[k - 1][j - 1] + calc(k , i);
                        s[i][j] = k;
                    }
                }
            }
        }
        cout << dp[n][m] << endl;
    }
    return 0;
}