[算法笔记]如何证明一个问题是NPC问题

步骤（Step）

在进入正题前，我想向大家讲解一下归约(reduction)、P和NP的概念。

期望（Desiderata’）：假如我们能够在多项式时间（polynomial-time）内解决问题Y，我们考虑能在当前的基础下解决其他哪些问题呢？

归约（Reduction）：当问题X能够在多项式时间内被归约为问题Y，并且对于任意问题X的样例能够被如下方式解决：
·多项式个标准的的算法复杂度计算步骤
·多项式次调用解决问题Y的步骤

标记（Notation）：X ≤ P Y. （当碰到这个标记时，通常可以理解为Y比X难，并且Y可以解X）

推论：
1）若X ≤ P Y并且Y可以再多项式时间内解决，那么X可以再多项式时间内解决
2）若X ≤ P Y并且X不可以在多项式时间内解决，那么Y也不能在多项式时间内解决
3）若X ≤ P Y并且Y≤ P X，记作X ≡ P Y。在这种情况下，X能够在多项式时间内被解决当且仅当Y可以在多项式时间内解决
P问题
定义（Definition）:一组每一个都拥有多项式算法的决策问题（即回答为是或否）通俗地说就是可以再多项式时间内解决的问题
NP问题
定义：一组每一个都存在多项式时间证书的（certifier）的决策问题。通俗地讲，就是在多项式时间可以被证明的问题。
所以P问题也是NP问题。所谓NPC问题也就是对于任意NP问题，都能够在多项式时间内归约成这个问题。也就是说比所有的NP问题都难（当然也有一样难的）
目前大多数学者认为NP问题真包含P问题，并且与NP-Hard问题有交集，交集即为NPC问题

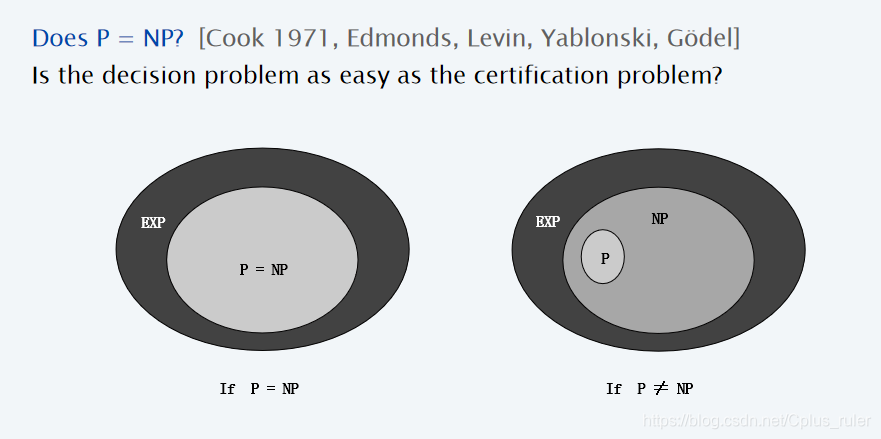
Figure 0

一、证明NP
首先，对任意NP问题，都能成为NPC问题，但是如果单独给我们一个问题，让我们证明它是NPC问题确实有些困难，所以我们取巧。记这个问题为Y,先证明这个问题是NP问题

二、构造
找一个NPC问题，记为X,证明：X ≤ P Y

三、解的充要性
证明：X有解当且仅当Y有解

例子（Example）

根据难度，我提供两个解题例子供大家参考
一、
假如你准备安排这学期的课程并且想要保证，冲突的课程数不超过K。你有了3个输入：C={…},S={…},R={ {…},{…},…}。C是一个包含不同课程的集合，S为所有课程可用的时间区间，R为学生的要求，包含了各个学生想要学的课程的集合（比如说有两个人，一个想学A,一个想学B,那么R={ {A},{B}}）。当两个课程被安排在一样的时间区间上发生冲突（即便有个学生两个都想学），证明这个问题是NPC问题

1.首先，对于任意的时间安排（作为证书。实际上，大多数证明证书都可以随便选，比如说你朋友的名字，虽然听起来非常离谱）。我们遍历所有学生的要求，并且检查他们的要求是否冲突了，并且数出冲突数目。最后检查总数是否小于K。以上的步骤可以再多项式时间内完成。（强烈建议把每一个步骤分开写，然后写上各自的复杂度）所以这个问题是NP。（证明多项式时间内可解，我们大多数时候都是选择最笨的方法，即遍历，然后证明遍历是多项式时间的）

2.我们选择三染色问题（3-Color问题。给一张图，用三种颜色给点染色，找一个染色方案，使得任意相邻的两点不同色）作为本题选中的NPC问题。对于任意三染色方案，记这张图为G,我们构造本题下的样例，：让每一个点代表一个课程，构造C；让（u,v）代表一个要求里有u,v的学生,构造R；让我们使用的颜色代表时间间隙，构造S;最后，设K为0

3.我们证明G为正确的三染色方案，当且仅当（C,S,R,K）为这个题目的正确的解：
LHS->RHS:若G为正确的三染色方案，那么按照课程的颜色安排他们。因为对于任意边（u,v），u和v会被不同的颜色染色，那么对于每一个学生，他的要求就不会被安排在相同的时间间隙下，这也意味着，这个方案是可行的

RHS->LHS:如果（C,S,R,K）是这个问题的解，那么将G中的点按照他们的时间间隙染色。因为K=0,那么对于所有学生，他们的要求之间没有冲突。这意味着对于每一条边（u,v），u和v不会被相同的颜色染色。所以这是三染色问题的一个正确染色方案。
综上，这个问题是NPC问题

是不是看的有点懵呢？这是我的作业里面比较难的一道题，所以大家不要灰心，下面给大家献上一道简单的题

二、4-COLOR

给定一个无向图和四种不同的颜色，我们能够提供一种染色方案，使得相邻的点颜色不同吗？证明4-COLOR问题是NPC问题

1.假设给定任意一种染色方案，首先将这个方案赋给G（O(|V|),V表示G的顶点数）,我们在图中遍历这种方案，每遍历一个点时，判断它是否和它的邻点同色，由于各点的度数至多为|V-1|,所以这一步的复杂度为O(|V-1||V|)。所以这个问题可以在给定证书时多项式时间内解决。

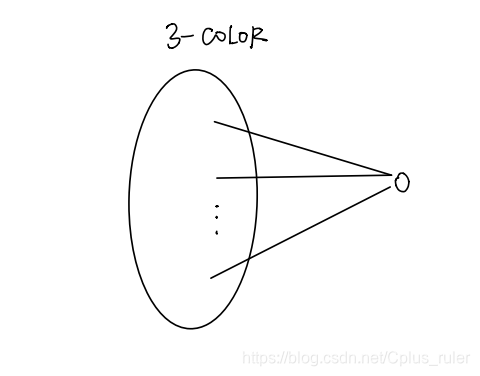
Figure 1
实际上，有这幅图就够了，但是保险起见，还是为大家解释一下，添加一个点（θ(1)），将这个点赋为第四种颜色（θ(1)），将这个点与G中的点全部相连（θ(|V|)），我们得到一个四染色样例
3.
LHS->RHS:若三染色样例为真，那么将新的点v加入G,得到一种四染色方案

RHS->LHS:若四染色样例为真，那么将v与它和G的连边删去，得到一种三染色。
以上是我的作业的中文版本，但是作为一个合格的CS专业的学生，我建议大家多看看英文方面材料。我将我的作业的原版本放在下面，供大家参考

Figure 2

做题经验

我建议大家在做类似题目和准备考试的时候，多准备几个NPC问题，毕竟虽然所有NP问题都可以归约为NPC问题，但是归约的难度显然是不一样的

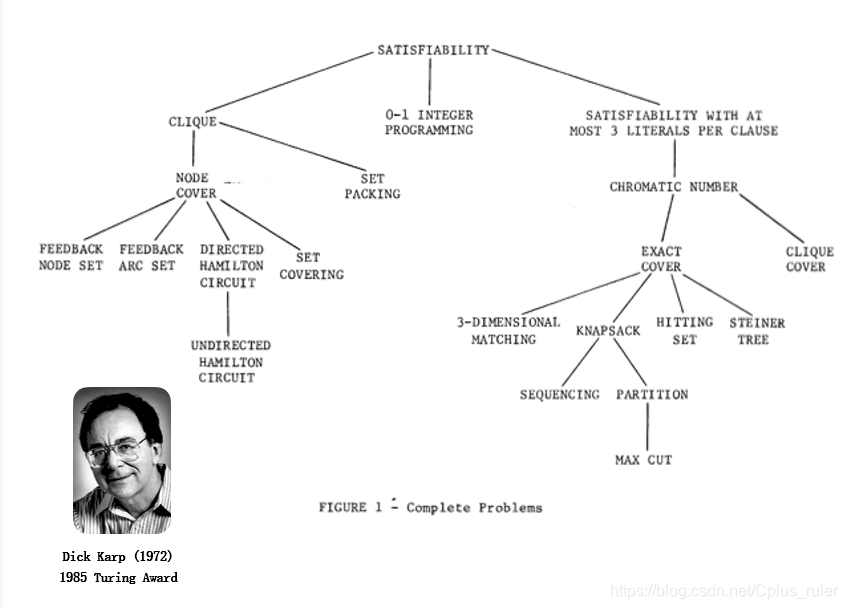
Figure 3

常见的有独立集（independent set）、集合覆盖（set cover）、顶点覆盖、哈密顿路（Hamilton road）、电路可满足性问题（circuit set,最古老的NPC问题）、团问题（clique）、旅行商问题、子集和问题（subset sum）、3-SAT（最经典的NPC问题）、三染色问题（3-C）还有一些其他的blablabla

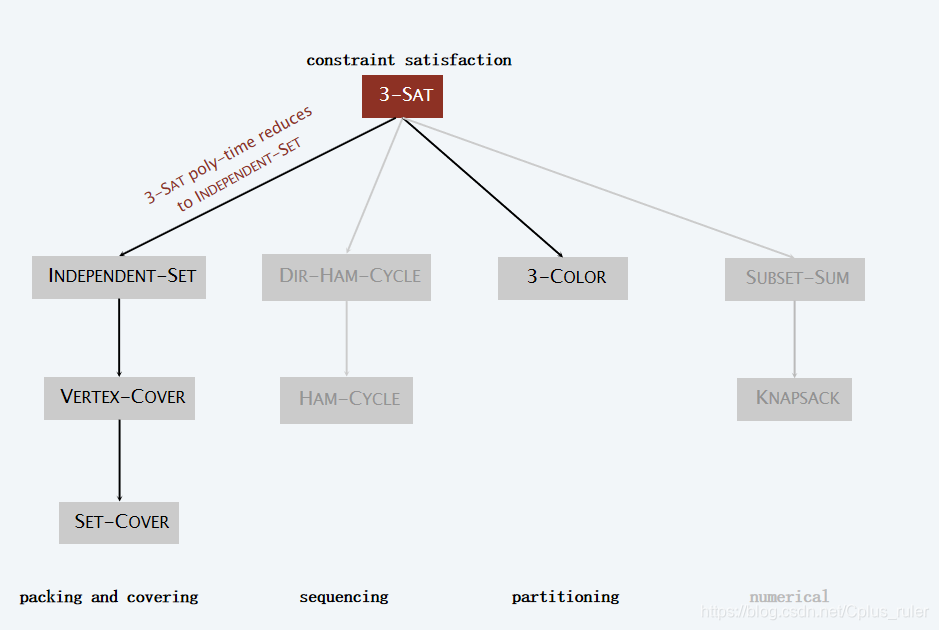
Figure 4

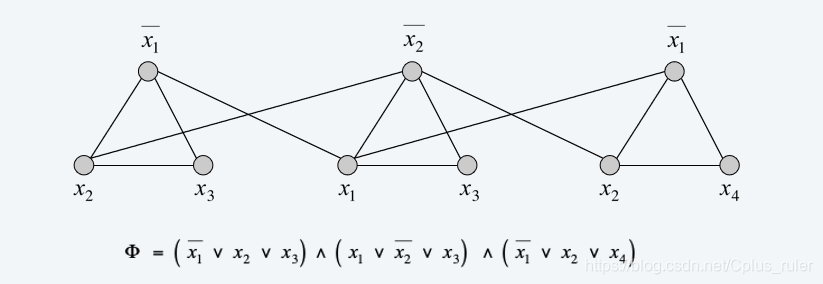
Figure 5 3-SAT

分析（Analysis）

一般来说决策问题（Decision problem）弱于搜索问题（Search problem）,而搜索问题弱于最优问题（Optimization problem）。但是这三者并没有无法逾越的界限。下面介绍一个例子
首先介绍一下顶点覆盖（Vertex cover），给定一个G=(V,E)和一个整数k,G的一个大小为k的顶点覆盖表示存在一个为k个点的子集，对任意G中的一条边，有一个点落在这个子集内部（用点覆盖所有的边）

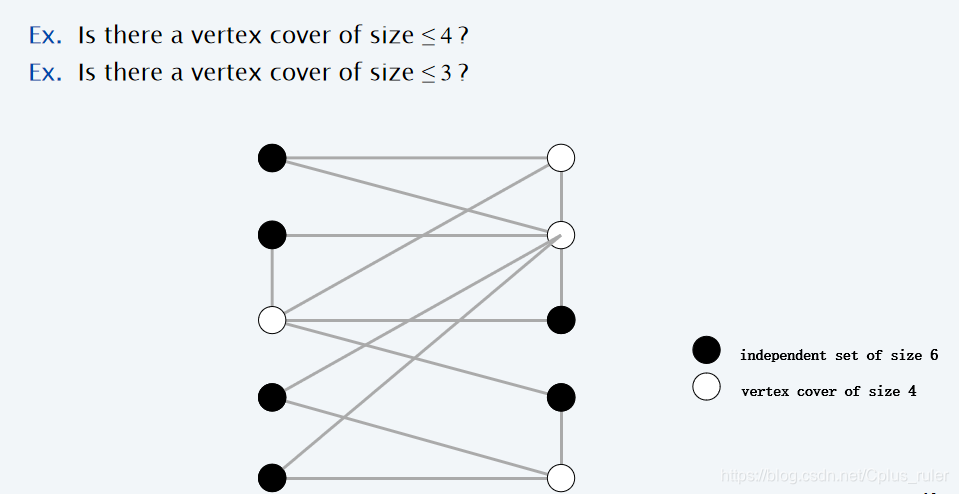
Figure 6
如在这个图中，就有一个大小为4的顶点覆盖（白点集）
回到我想要讲的例子中：对图G

1）决策问题：是否存在一个小于等于k的顶点覆盖

2）搜索问题：找一个小于等于k的顶点覆盖

3）最优问题：找到最小的顶点覆盖

首先显然地，如果有3）的解，那么2）、1）迎刃而解，如果有2）的解，那么1）有解。下面我们仔细思考这三个问题，也许它们之间的差距并非那么大。
假如我们能够解1），我们通过如下步骤解2），对于图G,我们拿掉一个点，来看这剩下的图中是否有小于等于k-1的顶点覆盖，由于拿掉的这个点有|V|中选择，故我们可以对于这|V|个子图分别解决上面的问题，重复上面的步骤，可以根据我们拿出的点得到2）的解
OK,我们已经看到1）与2）的差距并没有那么大了，无非是遍历的问题，我们可以用动态规划解决（注意到先取v_1再取v_2和先取v_2再去v_1是相同的），当然这会在后面介绍。
现在我们假设知道了2）的解法，想知道3）的解，这个更加简单，只需要取k,k-1…，直到t的时候发现G中不存在小于t的顶点覆盖，那么G的最小顶点覆盖就是t+1,并且可以在取t+1时找到解

总结（Sum up）

总之，NPC问题就是很难的问题，但是在证明的时候可以站在前人的肩膀上，用已有的NPC问题来证明，2021结束了，我在2019年许下的愿望之一就是五年内开个博客，这是我的第一篇，由于平时学业很忙，所以只有在假期才能写一点，虽然老师教了NPC问题，但是感觉学得并不是很深，有兴趣的兄弟们可以找点论文和书籍看一下，最后川宝倒了，祭奠一下川宝，呜呜呜