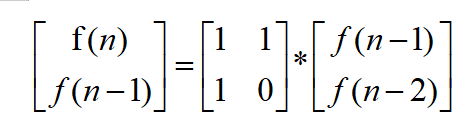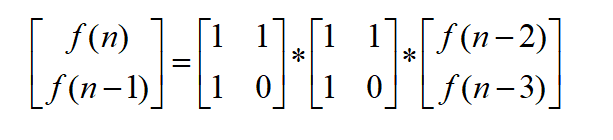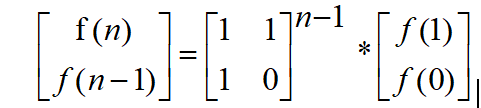说起矩阵快速幂学习的原因感觉比较low,源于斐波那契数列的递归算法的学习,个人认为当数据量较小的时候,递归是个不错的选择。
首先简单的介绍一下普通的递归算法:
下面是使用经典的递归算法
#include<iostream>
using namespace std;
int Fbi(int i)
{
if (i<2)
{
return i==0 ? 0:1;
}
return Fbi(i-1)+Fbi(i-2);
}
int main()
{
int n;
cin>>n;
cout<<Fbi(n)<<endl;
return 0;
}
我们简单的分析一下我们直接暴力使用递归求解斐波那契数列的时间复杂度
求解F(n),必须先计算F(i-1)和F(i-2),计算F(i-1)和F(i-2),又必须先计算F(i-3)和F(i-4)。。。。。。以此类推,直至必须先计算F(1)和F(0),然后逆推得到F(n-1)和F(n-2)的结果,从而得到F(n)要计算很多重复的值,在时间上造成了很大的浪费,算法的时间复杂度随着N的增大呈现指数增长,时间的复杂度为O(2^n),即2的n次方
是不是感觉非常不好呀!
所以这个算法在大数据的情况下肯定是不可取的,我们对这个算法做一个简单的优化一下。
优化一下:矩阵快速幂算法
我们小小的观察一下斐波那契函数的递推式
f(n)=f(n-1)+f(n-2)
假如我们两边同时加上一个f(n-1)
f(n)+f(n-1)=f(n-1)+f(n-1)+f(n-2)
我们简单的进行一下矩阵乘法就可以把原式变为下来的式子
简单的乘法运算规则我在这里就不介绍了,如果没有基础的线性代数知识大家可以去MOOC上简单的学习一下
我们再将上面的式子再进行一下简单的递推
…最后得到结果
这样的话我们就将斐波那契数列的矩阵乘法的表达式写出来了
然后我们在矩阵乘法当中找一下规律我们就能找到规律了
简单的用代码实现一下
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=1e9+9;
const int N=2;
ll tmp[N][N],res[N][N];
void multi(ll a[][N],ll b[][N],int n)
{
memset(tmp,0,sizeof(tmp));
for(ll i=0;i<n;i++)
{
for(ll j=0;j<n;j++)
{
for(ll k=0;k<n;k++)
{
tmp[i][j]+=(a[i][k]*b[k][j])%mod;
}
tmp[i][j]=tmp[i][j]%mod;
}
}
for(ll i=0;i<n;i++)
for(ll j=0;j<n;j++)
a[i][j]=tmp[i][j];
}
void Pow(ll a[][N],ll m,int n)
{
memset(res,0,sizeof(res));
for(ll i=0;i<n;i++) res[i][i]=1;
while(m)
{
if(m&1)
multi(res,a,n);
multi(a,a,n);
m>>=1;
}
}
int main()
{
ll m;
int n;
ll a[N][N];
while(~scanf("%lld",&m))
{
n=2;
a[0][0]=1,a[0][1]=1,a[1][0]=1,a[1][1]=0;
Pow(a,m,n);
cout<<res[1][0];
}
cout<<endl;
return 0;
}
虽然代码看起来复杂多了,但是我们再简单的进行一波时间复杂度的分析
,我们就会发现我们将其算法复杂度降到了log级了,大大降低了在大数时简单递归算法的时间复杂度。
好了,下次再分享关于矩阵快速幂的其他运用。