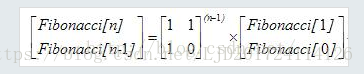用矩阵快速幂找斐波那契数列

说起斐波那契数列，相信大家都不会陌生，很好求是不是，那假如让你求第1e18个数字是多少，时间限制在1s，你怎么求？

参考文章：

https://blog.csdn.net/flyfish1986/article/details/48014523

https://blog.csdn.net/g_congratulation/article/details/52734306

https://blog.csdn.net/w20810/article/details/44041491

方法总比困难多，看完接下来写的，你就懂了。

先普及一下知识先：

一：矩阵相乘

若A为n×k矩阵，B为k×m矩阵，则它们的乘积AB(有时记做A·B)将是一个n×m矩阵。前一个矩阵的列数应该等于后一个矩阵的行数，得出的矩阵行数等于前一个矩阵的行数，列数等于后一个矩阵的行数。

其乘积矩阵AB的第i行第j列的元素为：

二：单位矩阵： n*n的矩阵 mat ( i , i )=1; 任何一个矩阵乘以单位矩阵就是它本身 n*单位矩阵=n，可以把单位矩阵等价为整数1。（单位矩阵用在矩阵快速幂中）

例如下图就是一个7*7的单位矩阵：

斐波那契(Fibonacci)数列

从第三项开始，每一项都是前两项之和。
=
+ ,

把斐波那契数列中相邻的两项和写成一个2
1的矩阵。F0=0, F1=1;

{F n F n - 1}

= {F n - 1 + F n - 2 F n - 1}

= {1 \times F n - 1 + 1 \times F n - 2 1 \times F n - 1 + 0 \times F n - 2}

= {1110} \times {F n - 1 F n - 2}

= {1110} n - 1 \times {F 1 F 0}

= {1110} n - 1 \times {10}

求F(n)等于求二阶矩阵的n - 1次方，结果取矩阵第一行第一列的元素。

下面来实现一个矩阵快速幂：

int pow(int n)//还是小范围数据来说吧,要不然返回值的类型自己定义
{
    mat c,res;
    memset(res.a,0,sizeof(res.a));
    c.a[0][0]=1;//给矩阵赋初值
    c.a[0][1]=1;
    c.a[1][0]=1;
    c.a[1][1]=0;
    for(int i=0;i<n;i++) res.a[i][i]=1;//单位矩阵；
    while(n)
    {
        if(n&1) res=mat_mul(res,c);//这里看就要用到上面的矩阵相乘了；
        c=mat_mul(c,c);
        n=n>>1;
    }
    return res.a[0][1];
}//时间复杂度log(n)

给出一道题吧：

定义f(0)=a,f(1)=b,f(n)=f(n-1)*f(n-2),给你a,b,n，求出f(n)%1000000007

分析：定义(x,y)，x代表a的个数，y代表b的个数。

先找规律f(0)=a (1,0)

f(1)=b; (0,1)

f(2)=ab (1,1)

f(3)=abb (1,2)

f(4)=abbab (2,3)

f(5)=abbababb (3,5)

f(6)=abbababbabbab (5,8)

......

由规律可知，f(n)=a^fibonacci(n-2)*b^fibonacci(n-1),但是n=500的时候fibonacci(500)就已经超过1e100了，又因为求的数要%1000000007，而1000000007是素数，由费马小定理可知：若p为素数，a^(p-1)≡1 (mod p)。a^b%p=(a^(k(p-1)+c))%p=(a^(k(p-1))*a^c)%p=a^c%p。所以f(n)=a^(fibonacci(n-2)%1000000006)*b^(fibonacci(n-1)%1000000006)%1000000007.

可看到1 1 2 3 5 8……为斐波那契数列，f[1]=1,f[2]=1;

{FnFn−1}={1110}n−2×{F2F1}={1110}n−2×{11}

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define mod 1000000007
typedef long long LL;
struct mat
{
    LL a[2][2];
};
mat mat_mul(mat x,mat y) ///矩阵相乘
{
    mat res;
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
        {
            res.a[i][j]=0; ///初始化
        for(int k=0;k<2;k++)
        res.a[i][j]=(res.a[i][j]+x.a[i][k]*y.a[k][j])%(mod-1);///此处只能模(mod-1),详情见上文
        }
    return res;
}
mat mat_pow(int n) ///矩阵快速幂
{
    mat c,res;
    c.a[0][0]=c.a[0][1]=c.a[1][0]=1; ///要乘的矩阵
    c.a[1][1]=0;
    res.a[0][0]=1,res.a[1][1]=1;///定义res为单位矩阵
    res.a[0][1]=res.a[1][0]=0;
    while(n)
    {
        if(n&1) res=mat_mul(res,c);
        c=mat_mul(c,c);
        n=n>>1;
    }
    return res;
}
LL pow(int a,int b ) ///很单纯的快速幂
{
    LL sum=1;
    while(b)
    {
        if(b&1) sum=(sum*a)%mod;
        a=a*a%mod;
        b=b>>1;
    }
    return sum;
}
int main()
{
    int n,fna,fnb,a,b;
    LL sum;
    while(~scanf("%d%d%d",&n,&a,&b)){
            if(n==0){
                printf("%lld\n",a%mod);
                continue;
            }
            else if(n==1){
                printf("%lld\n",b%mod);
                continue;
            }
            else if(n==2){
                printf("%lld\n",a*b%mod);
                continue;
            }

    mat result;

    result=mat_pow(n-2); ///计算n-2次

    fnb=result.a[0][0]*1+result.a[0][1]*1; ///与{ f[2] } 相乘,计算算出fib[n]与fib[n-1]
    fna=result.a[1][0]*1+result.a[1][1]*1; ///    f[1]

    sum=pow(a,fna)*pow(b,fnb)%mod;///a^f[n-1]*b^f[n]
    printf("fn=%d,fn_=%d\n",fna,fnb);
    printf("%lld\n",sum);

    }
   return 0;


}

再来一题：

链接：https://www.nowcoder.com/acm/contest/105/G
来源：牛客网

这是一个加强版的斐波那契数列。

给定递推式 $F(i) = \left\{ \begin{array} \\F(i-1) + F(i-2) + i^3 + i^2 + i + 1 & i>1 \\0 & i = 0 \\1 & i = 1\end{array}\right.$

求F(n)的值，由于这个值可能太大，请对10 ⁹+7取模。

输入描述:

第一行是一个整数T(1 ≤ T ≤ 1000)，表示样例的个数。
以后每个样例一行，是一个整数n(1 ≤ n ≤ 10¹⁸)。

输出描述:

每个样例输出一行，一个整数，表示F(n) mod 1000000007。

参考文章：

https://www.cnblogs.com/qldabiaoge/p/8971714.html

https://www.cnblogs.com/meditation5201314/p/8969754.html

这题是一题矩阵快速幂的模板题，表示第一次碰到矩阵快速幂然后就顺便学一下，其实和快速幂差不多。
矩阵快速幂的难点一般是构造矩阵，但是这题递推公式给了我们还是非常容易构造出矩阵的。
难题一般都是让我们自己去推公式，然后再通过公式写出所需要的矩阵。

递推公式给了我们，
就是要找到一个矩阵A【f(i),f(i-1),(i+1)^3,(i+1)^2,(i+1),1】 * A =【f(i-1),f(i-2),i^3,i^2,i,1】;
如果学过线代，这个是非常容易推出来的。
然后就通过矩阵的性质， F【n】=A^(n-1)*F【1】;

我们继续来分析上上个图的公式n - 1可通过乘矩阵来求F[n]，延伸一下
我要求本题的
F[n], F[n - 1], (i + 1) ^ 3, (i + 1) ^ 2, (i + 1), 1(即把i都增加1，和第一个公式一样) 所以就根据矩阵

f[i] = 1 1 1 1 1 1 f[i-1] 1->F[1]

f[i-1] = 1 0 0 0 0 0 f[i-2] 0->F[0]

(i+1)^3 = 0 0 1 3 3 1 i^3 8->2^3

(i+1)^2 = 0 0 0 1 2 1 * i^2 4->2^2

i + 1 = 0 0 0 0 1 1 i 2->2

1 = 0 0 0 0 0 1 1 1->1

设最后一列（蓝色）表示矩阵B，表示的是当i等于2时的结果，那这题我们要算F[n],只需算矩阵A的n-1次方，最后F[n]就是A矩阵和矩阵B相乘结果的第0行第0列的结果，

因为最后算出来的矩阵就是6行1列的，F[n]就是第0行第0列，代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define mod 1000000007
typedef long long LL;
struct mat
{
    LL a[6][6];
};
mat mat_mul(mat x,mat y) ///矩阵相乘
{
    mat rec;
    for(int i=0;i<6;i++)
        for(int j=0;j<6;j++)
    {
        rec.a[i][j]=0;
        for(int k=0;k<6;k++)
            rec.a[i][j]=(rec.a[i][j]+x.a[i][k]*y.a[k][j])%mod;
    }
    return rec;
}
LL mat_pow(LL n)
{
    mat c,rec;
    int num[6][6]={{1,1,1,1,1,1}, ///不能直接赋值
                    {1,0,0,0,0,0},
                    {0,0,1,3,3,1},
                     {0,0,0,1,2,1},
                     {0,0,0,0,1,1},
                     {0,0,0,0,0,1}};
        for(int i=0;i<6;i++)
            for(int j=0;j<6;j++)
            c.a[i][j]=num[i][j];
    memset(rec.a,0,sizeof(rec.a));
    for(int i=0;i<6;i++) ///定义一个单位矩阵
        rec.a[i][i]=1;
    while(n) ///快速幂
    {
        if(n&1) rec=mat_mul(rec,c);
        c=mat_mul(c,c);
        n=n>>1;
    }
    LL sum;
    sum=(rec.a[0][0]+rec.a[0][2]*8+rec.a[0][3]*4+rec.a[0][4]*2+rec.a[0][5])%mod;///最终结果
    return sum;
}
int main()
{
    LL n, ncase,result;
    scanf("%lld",&ncase);
    while(ncase--)
    {
        scanf("%lld",&n);
        result=mat_pow(n-1);
        printf("%lld\n",result%mod);
    }
    return 0;
}

over。