[XSY] 分割（dfs树）

分割
题目相当于问删掉两个点后图是否仍然连通
割点问题，考虑用dfs树解决
设删去点u，v（dfn[v]<dfn[u]）
把 u, v 删去之后整棵树大概断成了几个部分：
• v 上面到根的部分，以及上面挂着的那些东西，记作 $h i g h$ ；
• u 到 v 之间的那一段，以及上面挂着的那些东西，记作 $m i d$ ；
• u ，v的子树们，记作 $low_u$ ， $low_v$ 。
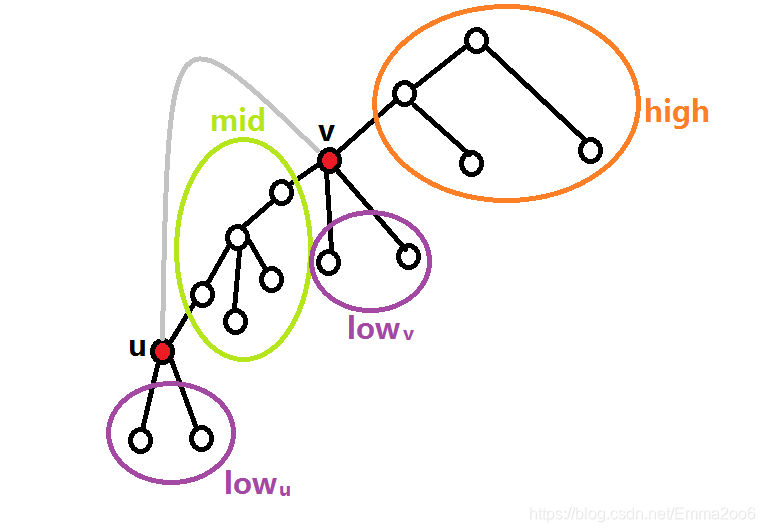
在这里插入图片描述
要保证删去u，v后图连通，则 $low_u$ ， $m i d$ ， $low_v$ 必须想办法和 $h i g h$ 连通

$low_v$ :每颗子树有非树边连接 $h i g h$
$low_u$ :每颗子树有非树边连接 $h i g h$ 或有非树边连接 $m i d$ 且 $m i d$ 有非树边连接 $h i g h$
$m i d$ :有非树边连接 $h i g h$ 或 有非树边连接 $low_u$ 的其中一颗子树，同时这颗子树有非树边连接 $h i g h$

当然， $f a [u] = = v$ 的情况略有不同，且 $v = = 1$ 时要特判

上面的思路除了加粗字体的情况没考虑到，其它都想到了
以下是想不出来的实现：

对于子树内有非树边连接 $h i g h$ 的条件：
预处理出 low[u] 表示以u为根的子树通过非树边最高能连到的位置

对于 $m i d$ 有非树边连接 $h i g h$ 的条件：
预处理出 g[u][k] 表示 u到其 $2^k$ 次祖先的这一段以及上面挂着的东西中，不算 u，通过非树边最高能到的位置（树上倍增）
（注意：g[u][0]!=low[fa[u]]，详见代码）

对于 $low_u$ 中有非树边连接 $m i d$ 的条件：
考虑转化一下条件，
原条件为 对于 $low_u$ 的任意一颗子树，若在[1,dfn[v]-1]中没有通过非树边能连到的位置，那么在[dfn[v]+1,dfn[u]-1]中至少有一个通过非树边能连到的位置
我们将其转化为 若 $low_u$ 中有一颗子树在[1,dfn[v]-1]和[dfn[v]+1,dfn[u]-1]中均没有通过非树边能连到的位置，那么边（u，v）不能删
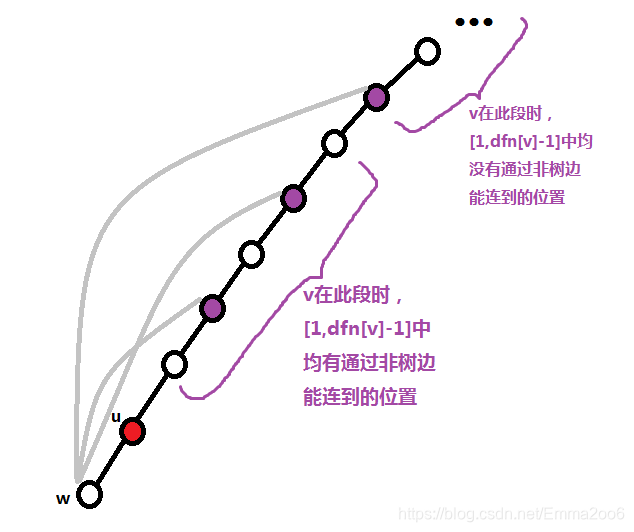
在这里插入图片描述
如图，w为u的其中一颗子树，标紫的点是w通过非树边能连到的位置中在u上方的部分，可以发现，只有v在low[w]及其往上的部分时，[1,dfn[v]-1]中才会没有w通过非树边能连到的位置，这时若[dfn[v]+1,dfn[u]-1]中没有其它w通过非树边能连到的位置，即dfn[w通过非树边第二高能连到的位置]>=dfn[u]，则（u，v）不能删

预处理出 slow[u] 表示以u为根的子树通过非树边第二高能连到的位置即可
（同学教的，妙啊！）

对于 $m i d$ 有非树边连接 $low_u$ 的其中一颗子树，同时这颗子树有非树边连接 $h i g h$ 的条件：
还是考虑转化条件，
原条件为 $low_u$ 中有一颗子树，在[1,dfn[v]-1]和[dfn[v]+1,dfn[u]-1]中均有其通过非树边能连到的位置
转化为对于 $low_u$ 的其中一颗子树，记 $l, r$ 为这棵子树通过非树边能连到的位置中在u上方部分的最高点和最低点，若 $l$ <=dfn[v]-1 且 $r$ >=dfn[v]+1，即 $l$ +1<=dfn[v]<= $r$ -1，那么（u，v）边的 $m i d$ 部分一定能通过连接这颗子树连到 $h i g h$

具体地， $l$ 即为low[son[u]]，
对每个点u维护一个优先队列，记录以u为根的子树通过非树边能连到的位置，pop出 son[u] 的优先队列中 dfn值>=dfn[u] 的位置即可找到 $r$ （优先队列合并）

对于最后两个条件，我一开始想的是暴力维护每个点u即它的子树通过非树边能连到的所有位置（以dfn序为下标建线段树，维护区间内能连接到的位置的个数（类似权值线段树的感觉）），然后合并线段树
虽然后来了解到合并线段树的时间复杂度是 $O (n l o g n)$ ，所以整道题的复杂度也就 $O(nlog^2n)$ ，即理论复杂度也是对的，但是常数过大，大概率会T

但是syh大佬通过把 判断对于确定的u,v，(u,v)是否可删 转化为 对于确定的u，寻找什么样的v满足(u,v) 可删/不可删，让这题有了简单许多的做法 $O r z$

Code:

#include<iostream>
#include<cstdio>
#include<map>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
const int N=3e5+5;
struct data{
    
    
    int v,nxt;
}edge[N<<1];
vector<int> vex[N],vid[N];
int n,m,cnt,head[N],ind,dfn[N],sz[N],son[N],fa[N][21];
int low[N],slow[N],g[N][21];
int st[N<<2];
int fl[N],hk[N];
//fl[u]=删掉u后，有几个u的子节点会被与连通图断开 
//hk[v]=删掉fa[v][0]后，v会与连通图断开 
map<int,int> mp[N];
//mp[a][b]=1表示为保持图连通，若删了a，则b不能被删 
bool fla[N],flagg[N];
int rt[N];
priority_queue<int> q[N];
queue<int> que;
void add(int u,int v){
    
    
    edge[++cnt].v=v;
    edge[cnt].nxt=head[u];
    head[u]=cnt;
}
void merge(int a,int b){
    
    
    int p[11];
    p[1]=low[a];p[2]=slow[a];p[3]=low[b];p[4]=slow[b];
    sort(p+1,p+5);
    low[a]=p[1];
    slow[a]=n+1;
    for(int i=2;i<=4;i++){
    
    
        if(p[i]!=p[i-1]){
    
    
            slow[a]=p[i];break;
        }
    }
}
inline void dfs(int u){
    
    
    ind++;
    dfn[u]=ind;
    for(int i=head[u];i;i=edge[i].nxt){
    
    
        if(!dfn[edge[i].v]){
    
    
            fa[edge[i].v][0]=u;
            dfs(edge[i].v);
    	}    
    }
}
void dfs_tree(int u){
    
    //判low直接与high连通+low通过mid与high连通 
	sz[u]=1;
    low[u]=dfn[u];slow[u]=n+1;
    for(int i=head[u];i;i=edge[i].nxt){
    
    
    	int v=edge[i].v;
        if(v==fa[u][0]) continue;
        if(fa[v][0]==u){
    
    
            son[u]++;
            dfs_tree(v);
            merge(u,v);
            sz[u]=sz[u]+sz[v];
            if(low[v]>=dfn[u]){
    
    
        		fl[u]++;hk[v]++;
    		}
			else if(slow[v]>=dfn[u]) mp[u][low[v]]=1;
        }
		else{
    
    
            if(dfn[v]==low[u]) continue;
            if(low[u]>dfn[v]){
    
    
                slow[u]=low[u];
                low[u]=dfn[v];
            }else if(slow[u]>dfn[v]) slow[u]=dfn[v];
        }
    }
}
//此时的线段树用于统计low的最小值 
inline void update(int u,int l,int r,int x,int v){
    
    
    if(l>x||r<x)return;
    if(l==r){
    
    
        st[u]=v;
        return;
    }
    int mid=(l+r)/2;
    update(u<<1,l,mid,x,v);
    update(u<<1|1,mid+1,r,x,v);
    st[u]=min(st[u<<1],st[u<<1|1]);
}
inline int query(int u,int l,int r,int ql,int qr){
    
    
    if(l>qr||r<ql)return n+1;
    if(ql<=l&&r<=qr)return st[u];
    int mid=(l+r)/2;
    int res1=query(u<<1,l,mid,ql,qr);
    int res2=query(u<<1|1,mid+1,r,ql,qr);
    return min(res1,res2);
}
//此时的线段树用于维护区间是否可选 
inline void modify(int u,int l,int r,int ql,int qr){
    
    
    if(!flagg[u]){
    
    
        que.push(u);
        flagg[u]=1;
    }
    if(l>qr||r<ql)return;
    if(ql<=l&&r<=qr){
    
    
        st[u]=1;
        return;
    }
    int mid=(l+r)/2;
    modify(u<<1,l,mid,ql,qr);
    modify(u<<1|1,mid+1,r,ql,qr);
    st[u]=st[u<<1]&st[u<<1|1];
}
inline bool ask(int u,int l,int r,int x){
    
    
    if(l>x||r<x) return 0;
    if(st[u]) return st[u];
    if(l==r) return st[u];
    int mid=(l+r)/2;
    return ask(u<<1,l,mid,x)|ask(u<<1|1,mid+1,r,x);
}
inline void get_g(int u){
    
    //判mid不通过low直接与high连通  
    for(int i=1;i<=20;i++){
    
    
        fa[u][i]=fa[fa[u][i-1]][i-1];
        g[u][i]=min(g[u][i-1],g[fa[u][i-1]][i-1]);
    }
    int sum=0,tot=0,s=n+1;
    for(int i=head[u];i;i=edge[i].nxt){
    
    
    	int v=edge[i].v;
        if(v==fa[u][0]) continue;
        if(fa[v][0]==u) sum++;
        else s=min(s,dfn[v]);
    }
    for(int i=head[u];i;i=edge[i].nxt){
    
    
    	int v=edge[i].v;
        if(fa[v][0]==u){
    
    
            tot++;
            update(1,1,sum,tot,low[v]);
        }
    }
    tot=0;
    for(int i=head[u];i;i=edge[i].nxt){
    
    
    	int v=edge[i].v;
        if(fa[v][0]==u){
    
    
            tot++;
            g[v][0]=min(min(query(1,1,sum,1,tot-1),query(1,1,sum,tot+1,sum)),s);
        }
    }
    for(int i=head[u];i;i=edge[i].nxt){
    
    
    	int v=edge[i].v;
        if(fa[v][0]==u) get_g(v);
    }
}
int solve(int u,int v){
    
    
    int s=n+1;
    for(int i=20;i>=0;i--){
    
    
        if(dfn[fa[v][i]]>dfn[u]){
    
    
            s=min(s,g[v][i]);
            v=fa[v][i];
        }
    }
    return s;
}
int mergeq(int a,int b){
    
    
    if(q[a].size()<q[b].size()) swap(a,b);
    while(!q[b].empty()){
    
    
        q[a].push(q[b].top());
        q[b].pop();
    }
    return a;
}
inline void getans(int u){
    
    //判mid通过low与high连通 
    for(int i=head[u];i;i=edge[i].nxt){
    
    
    	int v=edge[i].v;
    	if(fa[v][0]==u) getans(v);
	}	
    rt[u]=u;
    for(int i=head[u];i;i=edge[i].nxt){
    
    
    	int v=edge[i].v;
        if(v==fa[u][0])continue;
        if(fa[v][0]==u){
    
    
            int l=low[v],r=0;
            while(!q[rt[v]].empty()){
    
    
                if(q[rt[v]].top()>=dfn[u]) q[rt[v]].pop();
                else{
    
    
                    r=q[rt[v]].top();
                    break;
                }
            }
            modify(1,1,n,l+1,r-1);
			//对于非树边(u,y)（dfn[y]<dfn[u]）,若dfn[y]在[l+1,r-1]的区间内，则删去此边后(u,y)边的mid部分仍与high连通 
            rt[u]=mergeq(rt[v],rt[u]);
        }
		else{
    
    
            q[rt[u]].push(dfn[v]);
        }
    }
    for(int i=0;i<vex[u].size();i++){
    
    
        int x=u;
        int y=vex[u][i];
        int z=vid[u][i];
        if(dfn[y]>dfn[x])continue;
        if(x==1||y==1)continue;
        if(y==fa[x][0])continue;
        if(!ask(1,1,n,dfn[y]))fla[z]=1;
    }
    while(!que.empty()){
    
    
        flagg[que.front()]=0;
        st[que.front()]=0;
        que.pop();
    }//恢复 
}
char check(int id,int a,int b){
    
    
    if(dfn[a]>dfn[b]) swap(a,b);
    if(a==1){
    
    
        if(fa[b][0]==a){
    
    
            if(son[a]>2) return '1';
            if(son[a]>1&&sz[b]>1) return '1';
            if(son[b]>1) return '1';
            return '0';
        }
        if(son[a]>1) return '1';
        if(mp[b][dfn[a]]==0&&fl[b]==0) return '0';
        return '1';
    }
    if(fa[b][0]==a){
    
    
        if(sz[b]==1&&hk[b]==1){
    
    
            if(fl[a]<=1&&fl[b]==0&&mp[b][dfn[a]]==0) return '0';
        }
		else{
    
    
            if(fl[a]==0&&fl[b]==0&&mp[b][dfn[a]]==0) return '0';
        }
        return '1';
    }
    if(fl[a]||fl[b]||mp[b][dfn[a]]) return '1';
    int s=solve(a,b);
    if(s>=dfn[a]&&fla[id]) return '1';
    return '0';
}
int main(){
    
    
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
    
    
    	int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
        vex[x].push_back(y);
        vex[y].push_back(x);
        vid[x].push_back(i);
        vid[y].push_back(i);
    }
    dfs(1);
    dfs_tree(1);
    get_g(1);
    for(int i=1;i<=n*4;i++) st[i]=0;
    getans(1);
    for(int i=1;i<=m;i++)
        putchar(check(i,edge[i*2-1].v,edge[i*2].v));
}

[XSY] 分割（dfs树）

猜你喜欢