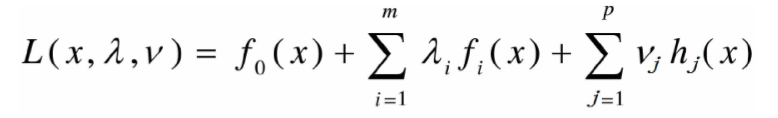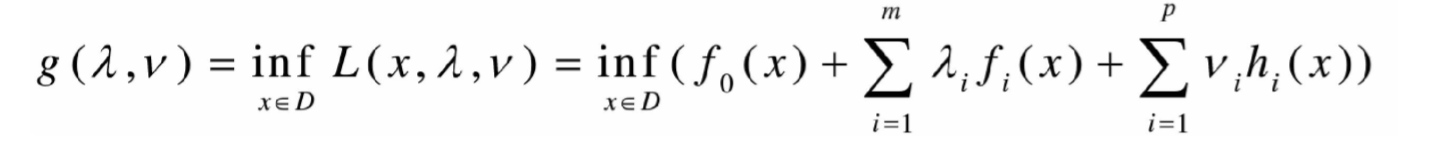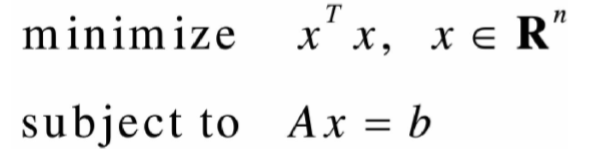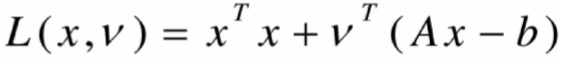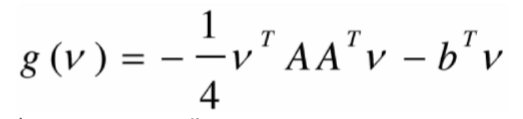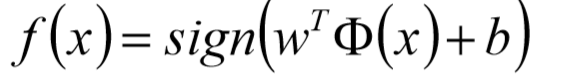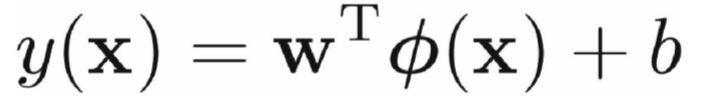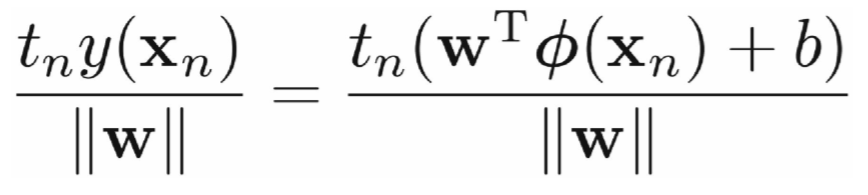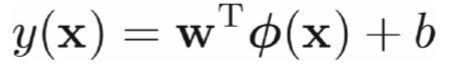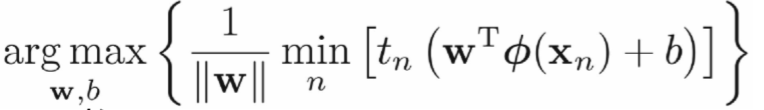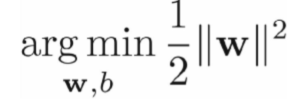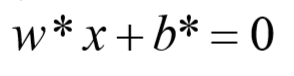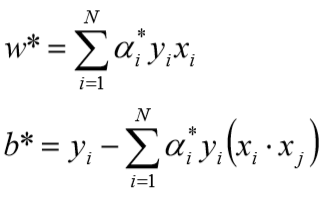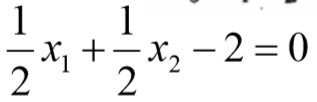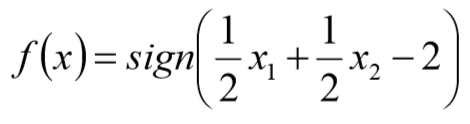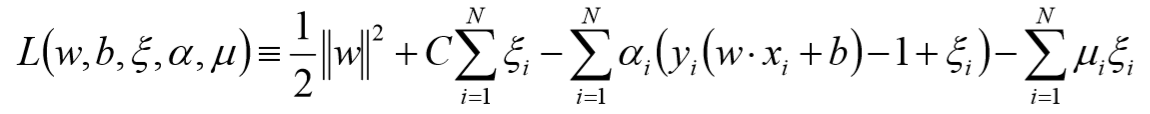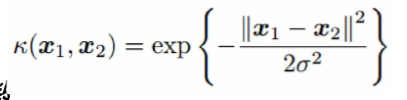目录
对偶问题
- 一般优化问题的Lagrange乘子法
- Lagrange函数
对固定的x,Lagrange函数L(x,λ,v)为关于λ和v 的仿射函数
Lagrange对偶函数(dual function
- Lagrange对偶函数
- 若没有下确界,定义:
- 根据定义,显然有:对∀λ>0,∀v,若原优化问 题有最优值p*,则
- 进一步:Lagrange对偶函数为凹函数。
线性方程的最小二乘问题
- 原问题
- Lagrange函数
- Lagrange对偶函数
对L求x的偏导,带入L
对g求v的偏导
强对偶条件
- 若要对偶函数的最大值即为原问题的最小 值,考察需要满足的条件:
Karush-Kuhn-Tucker (KKT)条件
主要内容和目标
- 理解支持向量机SVM的原理和目标
- 掌握支持向量机的计算过程和算法步骤
- 对线性不可分的数据,理解软间隔最大化的 含义
- 了解核函数的思想
- 了解SMO算法的过程
支撑超平面
- 设集合C,x0为C边界上的点。若存在a≠0, 满足对任意x∈C,都有 成立,则称 超平面 为集合C在点x0处的支 撑超平面。
- 凸集边界上任意一点,均存在支撑超平面。
- 反之,若一个闭的非中空(内部点不为空)集 合,在边界上的任意一点存在支撑超平面, 则该集合为凸集。
分割超平面
- 设C和D为两不相交的凸集,则存在超平面 P,P可以将C和D分离。
- 注意上式中可以取等号:
所以:逆命题:“若两个凸集C和D的分割超平面 存在,C和D不相交”为假命题。
加强条件:若两个凸集至少有一个是开集,那 么当且仅当存在分割超平面,它们不相交。
分割超平面的构造
- 两个集合的距 离,定义为两个 集合间元素的最 短距离。
- 做集合C和集合D 最短线段的垂直 平分线。
分割超平面的思考
- 如何定义两个集合的“最优”分割超平面?
找到集合“边界”上的若干点,以这些点为“基础” 计算超平面的方向;以两个集合边界上的这些 点的平均作为超平面的“截距”
- 若两个集合有部分相交,如何定义超平面, 使得两个集合“尽量”分开?
注:上述“集合”不一定是凸集,可能是由若干离 散点组成。若一组集合为(x,1),另一组集合为 (x,2),则为机器学习中的分类问题。
线性分类问题
输入数据
- 假设给定一个特征空间上的训练数据集 T={(x1,t1), (x2,t2)…(xN,tN)}
其中,xi∈Rn,ti∈{+1,-1},i=1,2,…N。
- xi为第i个实例(若n>1, xi为向量);
- ti为xi的类标记;
当ti=+1时,称xi为正例;
当ti=-1时,称xi为负例;
- (xi,ti)称为样本点。
各种概念
- 线性可分支持向量机
硬间隔最大化hard margin maximization
硬间隔支持向量机
-
线性支持向量机
软间隔最大化soft margin maximization
软间隔支持向量机
- 非线性支持向量机
核函数kernel function
注:以上概念的提法,各个文献并不十分统一。
线性可分支持向量机
- 给定线性可分训练数据集,通过间隔最大化得到的 分离超平面为
- 相应的分类决策函数
- 该决策函数称为线性可分支持向量机。
- φ(x)是某个确定的特征空间转换函数,它的作用是 将x映射到(更高的)维度。
最简单直接的:φ(x)=x
- 稍后会看到,求解分离超平面问题可以等价为求解 相应的凸二次规划问题。
整理符号
- 分割平面:
- 训练集:
- 目标值:
- 新数据的分类:
二维平面上线性分类问题
线性可分支持向量机
使用(高斯)核,解决线性不可分
- 粗线是分割超“平面”
- 其他线是y(x)的等高线
- 绿色圈点是支持向量点
推导目标函数
- 根据题设,
- w,b等比例缩放,则t*y的值同样缩放,从 而:
最大间隔分离超平面

- 目标函数:
函数间隔和几何间隔
目标函数:
总可以通过等比例缩放w的方法,使得两类 点的函数值都满足| y |≥1
建立目标函数
- 总可以通过等比例缩放w的方法,使得两类 点的函数值都满足| y |≥1
- 约束条件:
- 原目标函数:
- 新目标函数:
建立目标函数:(若不考虑核函数)
拉格朗日乘子法
- 原问题是极小极大问题
- 原始问题的对偶问题,是极大极小问题
- 将拉格朗日函数L(w,b,a)分别对w,b求偏导 并令其为0:
- 代入L(w,b,α)中,得到:
继续求minw,bL(w,b,α)对α的极大
整理目标函数:添加负号
线性可分支持向量机学习算法
- 构造并求解约束最优化问题
- 求得最优解α*
线性可分支持向量机学习算法
- 计算
- 求得分离超平面
- 分类决策函数
举例
- 给定3个数据点:正例点x1=(3,3)T,x2= =(4,3)T,负例点x3=(1,1) T,求线性可分支 持向量机。
- 目标函数:
分离超平面
- α1=α3=1/4对应的点x1,x3是支持向量。
- 带入公式:
- 得到w1=w2=0.5,b=-2
- 因此,分离超平面为
- 分离决策函数为
线性SVM的目标函数
拉格朗日函数
- 对w,b, ξ求偏导
带入目标函数
- 将三式带入L中,得到
- 对上式求关于α的极大,得到:
最终的目标函数
- 整理,得到对偶问题:
线性支持向量机学习算法
- 构造并求解约束最优化问题
- 求得最优解α*
线性支持向量机学习算法
- 计算
注意:计算b*时,需要使用满足条件0<αj<C的向量
实践中往往取支持向量的所有值取平均,作为b*
- 求得分离超平面
- 分类决策函数
损失函数分析
- 黑色:误分类率
- 蓝色: SVM合页损失
- 绿色:误差平方和
核函数
- 可以使用核函数,将输入空间映射到特征空间,从 而,使得原本线性不可分的样本可以在特征空间可 分。
- 在实际应用中,往往依赖先验领域知识才能选择有 效的核函数
- 多项式核函数
- 高斯核函数
- 字符串核函数
如:两个字符串的字符串编辑距离
将文档使用TF-INF转换成向量,然后求向量夹角余弦
核函数映射
高斯核
- 粗线是分割超“平面”
- 其他线是y(x)的等高线
- 绿色圈点是支持向量点
SVM中系数的求解:SMO
- 序列最小最优化
Sequential Minimal Optimization
- 有多个拉格朗日乘子
- 每次只选择其中两个乘子做优化,其他因子 认为是常数
将N个解问题,转换成两个变量的求解问题:并 且目标函数是凸的。
SMO
- 考察目标函数,假设α1和α2是变量,其他 是定值:
二变量优化问题
SMO的迭代公式
- 迭代公式:
SMO算法
- 取初值α(0)=0,令k=0
- 选择优化变量α1(k),α2(k),解析求解两个 变量的优化问题,求得最优解α1(k+1), α2(k+1),更新α为α(k+1)
- 若在精度ε范围内满足退出条件(下一 页),则转4;否则,k++,转2
- 取α=α(k+1)