\(\;\)
前置知识:线段树。
相关知识:可持久化Trie,具体可以看我的博客。其中对可持久化的概念有具体说明。
这里先介绍一个东东————权值线段树
\(\;\)
权值线段树
\(\;\)
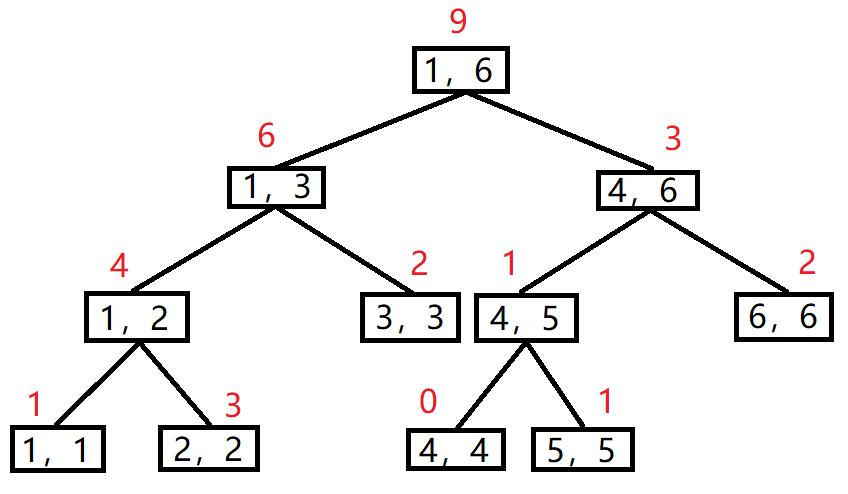
权值线段树:顾名思义,是以数值为下标建立的一颗线段树,大概类似于桶,如图:
\(\;\)
在这个例子中,我们插入了\(1,2,2,2,3,3,5,6,6\)这些数,因此可以发现,权值线段树中一个节点的数值即为:在这个节点的值域中数的数量。
\(\;\)
主席树
\(\;\)
根据可持久化的思想:每次只记录发生变化的部分。而以区间和为例,每次修改至多会使\(log(n)\)个区间所对应的节点发生变化。
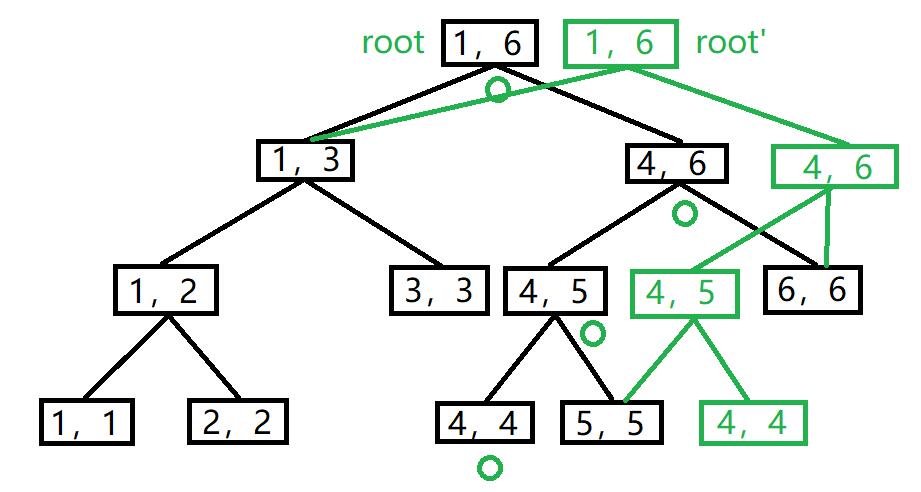
因此对于每个发生变化的节点\(p\),创建一个新版本\(p'\),而只要\(p\)不是叶子节点,它的左右儿子之一必定发生了更新。不妨设变化的是左儿子,那么我们只需把右儿子的信息拷贝过来,再向左子树\(lson\)递归,返回时令\(p'\)的左儿子为更新后的\(lson'\)。看下面的例子:
\(\;\)
\(\;\)
我们把\(4\)这个位置修改了,会使\([4,4],[4,5],[4,6],[1,6]\)这\(4\)个节点所对应的区间发生变化,可以对照参考一下。
由于主席树不再是一颗完全二叉树,所以我们不能用\(2x,2x+1\)这样的层次序编号,而是改为记录左右儿子的编号,其实与Trie中的字符指针类似。所以在插入查询操作时,我们要把\(l,r\)(这个区间对应的左右端点),当作函数的参数传递。
因为它每次修改只会新增\(log(n)\)个节点,所以主席树的空间复杂度为:\(O(n+m\;log\;n)\),其中\(m\)为版本个数
而对于第\(i\)个版本的线段树,从它的根\(root[i]\)向下遍历,即可得到这个版本所对应的信息。
下面看看主席树可以解决什么问题。
\(\;\)
Problem 1 ————静态区间第k小
题意
\(\;\)
给定一个长度为\(n\)的序列,共有\(m\)次询问,每次询问给定\(l,r,k\),求\([l,r]\)这段区间的第\(k\)小数。
\(n,m\leq 10^5,a[i]\leq 10^9\)
题目地址: https://www.luogu.com.cn/problem/P3834
暴力显而易见的超时。相信大家也都会写,这里不多赘述。
\(\;\)
整体二分
\(\;\)
首先,我们不考虑\(l,r\)的限制,在\([1,n]\)的区间如何找第\(k\)小数?
容易想到我们可以建立一颗权值线段树。而我们在查询的过程中,只需判断\([L,mid]\)这个值域中数的数量\(cnt\)与\(k\)的大小关系:
若\(cnt\geq k\),显然第\(k\)小数在\([L,mid]\)这段值域中。
否则说明是在\([mid+1,R]\)这段值域中。
而这里要注意的是,由于\(a[i]\)很大,所以我们先将其离散化,再进行操作。
\(\;\)
前缀和
\(\;\)
但现在有\(l,r\)的限制,如何做?
于是我们可以建立一颗主席树,在输入这个序列的时候不断新建版本,可以发现第\(i\)个版本的线段树维护的是\([1,i]\)这段区间的信息。
另外,还有一个重要的性质:主席树的每个版本的对值域的划分是相同的。
换句话来说:除了节点信息\(cnt\)发生变化,两颗线段树的内部结构,与和每个节点所代表的值域区间完全对应。
所以我们可以发现:第\(r\)版本的值域区间\([L,R]\)的\(cnt\)减去第\(l-1\)版本的值域区间\([L,R]\)的\(cnt\)。即为:\(a[l-r]\)中有多少个数是落在值域\([L,R]\)中的。那么我们只需从\(root[l-1]\)与\(root[r]\)同时出发进行访问,利用这种前缀和的性质,即可算出答案。
\(\;\)
code
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, m, idx, a[N], root[N];
vector <int> G;
struct Segtree
{
int l, r, cnt;
}tree[N * 25]; //注意:每次新建一个版本都要新增log(n)个节点,因此空间要开够
int Getit(int x)
{
return lower_bound(G.begin(), G.end(), x) - G.begin();
//找到x这个数在序列中的排名
}
int build(int l,int r)
{
int rt = ++ idx; //新建一个节点
if(l == r)
{
return rt;
}
int mid = (l + r) >> 1;
tree[rt].l = build(l, mid); tree[rt].r = build(mid + 1, r);
// 左右儿子也附上编号
return rt;
}
int Insert(int Last,int l,int r,int x)
{
int Now = ++ idx; // 新建一个节点
tree[Now] = tree[Last]; //先把原先的拷贝过来
if(l == r) // 若为叶子节点
{
tree[Now].cnt ++; //这个位置上数的数量 + 1
return Now; //返回这个点的编号
}
int mid = (l + r) >> 1;
if(x <= mid)
{
tree[Now].l = Insert(tree[Last].l, l, mid, x);
// 若修改的在左子树,则往左子树递归插入新节点
}
else
{
tree[Now].r = Insert(tree[Last].r, mid + 1, r, x);
//否则就在右子树
}
tree[Now].cnt = tree[tree[Now].l].cnt + tree[tree[Now].r].cnt;
//push up
return Now;
}
int Query(int Last,int Now,int l,int r,int k)
{
if(l == r)
{
return l; //若为叶子节点,则第k小的数显然就是这个
}
int mid = (l + r) >> 1;
int ch = tree[tree[Now].l].cnt - tree[tree[Last].l].cnt;
//[l,r]这段区间在左子树值域的数量
if(k <= ch) // 若左子树的数量已至少有k个了,往左子树递归
return Query(tree[Last].l, tree[Now].l, l, mid, k);
else //否则就往右子树递归,注意在右子树中的排名为 k - ch (左子树已有ch个了)
return Query(tree[Last].r, tree[Now].r, mid + 1, r, k - ch);
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
G.push_back(a[i]);
}
sort(G.begin(),G.end());
G.erase(unique(G.begin(),G.end()),G.end()); // 离散化
root[0] = build(0 , G.size() - 1); //建树
//将区间左右端点[0,G.size()-1]当作参数传递
for(int i = 1; i <= n; i++)
{
root[i] = Insert(root[i - 1], 0, G.size() - 1, Getit(a[i]));
//每次输入插入一个新的版本
}
while(m--)
{
int l, r, k;
scanf("%d%d%d",&l,&r,&k);
printf("%d\n",G[Query(root[l - 1], root[r], 0, G.size() - 1, k)]);
//对于每次询问输出这个排名为k的数值(在G里存储的)
}
return 0;
}
\(\;\)
Problem 2 ————动态区间第k小
题意
\(\;\)
给定一个含有\(n\)个数的序列\(a_1,a_2,\cdots,a_n\),需要支持两种操作
1.\(\;Q\;l\;r\;k\):表示查询下标在区间\([l,r]\)中第\(k\)小的数
2.\(\;C\;x\;y\):表示将\(a_x\)改为\(y\)
\(n,m\leq 10^5,a_i\leq 10^9\)
题目地址: https://www.luogu.com.cn/problem/P2617
\(\;\)
与上道题相比只多了修改操作(废话)
\(\;\)
树状数组维护
\(\;\)
我们考虑把\(a_x\)改为\(y\)的影响,设\(a_x\)原先等于\(v\),显然,第\(x\)到\(n\)个版本的线段树下标为\(y\)的值要\(+1\),为\(v\)的要\(-1\)
如果只是单纯的\(for(x\;to\;n)\),然后对这些线段树进行修改的话,很明显:每次修改的复杂度是\(O(n\;log\;n)\),而\(m\)次操作,时间复杂度为\(O(nm\times log\;n)\),显然不行。
所以我们考虑如何优化这个东西。
与上题相同我们想要知道的是\(sum[r]-sum[l-1]\)这样的区间和。
如果仔细观察你就可以发现,这个东西可以用树状数组的思路来做。
在这里:以\(root[x]\)为根的线段树存储的不再是\([1,x]\)的信息了,而是\([x-lowbit(x)+1,x]\)中的信息。
而根据树状数组的套路,每次修改会对\(log(n)\)个点产生影响,查询也是同理。
通俗点说:就是把每颗线段树当做一个点,这样就形成了一个长度为\(n\)的序列,然后再用树状数组维护这个序列的修改查询操作。(外层是树状数组,内层是线段树)
而每次至多修改\(log(n)\)个点(线段树),每个线段树修改的复杂度为\(log(n)\)。
由此可得,时间复杂度:\(O(m\times log_2 n)\)。
而空间复杂度?由于每次修改都至多新建\(log_2 n\)个点,所以为\(O((n+m)\times log_2 n)\)
剩下的东西就和Problem 1完全一样了。
\(\;\)
code
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, q, a[N], len, ask_x[N], ask_y[N], ask_k[N], tmp1[100], tmp2[100];
int root[N << 1], idx, cnt1, cnt2, g[N << 1];
struct Node
{
int l, r, cnt;
}tree[N * 400]; //注意要开到O((n+m) log2 n)的大小
int lowbit(int x)
{
return x&-x;
}
int Getit(int x)
{
return lower_bound(g + 1, g + len + 1, x) - g;
}
int Update(int Last,int l,int r,int x,int v)
{
//函数的意义:对线段树中下标为x的值加上v
int Now = ++idx; tree[Now] = tree[Last];
if(l == r)
{
tree[Now].cnt += v;
return Now;
}
int mid = (l + r) >> 1;
if(x <= mid)
{
tree[Now].l = Update(tree[Now].l, l, mid, x, v);
}
else tree[Now].r = Update(tree[Now].r, mid + 1, r, x, v);
tree[Now].cnt = tree[tree[Now].l].cnt + tree[tree[Now].r].cnt;
return Now;
}
inline void Add(int x,int val,int v)
{
for(;x <= n; x += lowbit(x))
{
root[x] = Update(root[x], 1, len, val, v);
//修改时,所有被它影响的线段树中下标为x的值都要加上v
}
}
int Query(int l,int r,int k)
{
if(l == r)
{
return l;
}
int mid = (l + r) >> 1, sum = 0;
for(register int i=1;i<=cnt1;i++)
{
sum -= tree[tree[tmp1[i]].l].cnt;
}
for(register int i=1;i<=cnt2;i++)
{
sum += tree[tree[tmp2[i]].l].cnt;
}
//sum就是维护一个前缀和,只不过使用树状数组算的
if(sum >= k)
{
for(register int i=1;i<=cnt1;i++)
{
tmp1[i] = tree[tmp1[i]].l;
}
for(register int i=1;i<=cnt2;i++)
{
tmp2[i] = tree[tmp2[i]].l;
}
return Query(l, mid, k);
}
else
{
//跟着向下遍历
for(register int i=1;i<=cnt1;i++)
{
tmp1[i] = tree[tmp1[i]].r;
}
for(register int i=1;i<=cnt2;i++)
{
tmp2[i] = tree[tmp2[i]].r;
}
return Query(mid + 1, r, k - sum);
}
}
int main()
{
scanf("%d%d",&n,&q);
for(register int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
g[ ++ len] = a[i];
}
char op[2];
for(register int i=1;i<=q;i++)
{
scanf("%s%d%d",op,&ask_x[i],&ask_y[i]);
if(op[0] == 'C')
{
ask_k[i] = 0;
g[ ++ len] = ask_y[i];
}
else
{
scanf("%d",&ask_k[i]);
}
}
sort(g + 1, g + len + 1);
len = unique(g + 1, g + len + 1) - g - 1;
for(register int i=1;i<=n;i++)
{
Add(i, Getit(a[i]), 1); //在i这个版本的线段树上a[i]离散化后的上的值加上1
}
for(register int i=1;i<=q;i++)
{
if(ask_k[i] == 0)
{
Add(ask_x[i], Getit(a[ask_x[i]]), -1);
a[ask_x[i]] = ask_y[i];
Add(ask_x[i], Getit(a[ask_x[i]]), 1);
}
else
{
cnt1 = 0, cnt2 = 0;
int L = ask_x[i] - 1, R = ask_y[i];
for(;L; L ^= lowbit(L)) //这里预处理出我们要算的是哪些版本的线段树
{
tmp1[ ++ cnt1 ] = root[L];
}
for(;R; R ^= lowbit(R))
{
tmp2[ ++ cnt2 ] = root[R];
}
printf("%d\n",g[Query(1, len, ask_k[i])]); //输出排名为k的值
}
}
return 0;
}