方差分析表和回归分析表的解读
各种统计量检验的决策准则
各种假设检验的假设的建立
第十一章 一元线性回归
11.1 变量间的关系的度量
11.1.1 变量间的关系
- 函数关系:设有两个x和y,y随x一起变化,并完全依赖于x,y是x的函数, y = f ( x ) y = f(x) y=f(x),x为自变量,y为因变量。
- 相关关系:变量之前存在的不确定的关系称为相关关系。
- 一个变量的取值不能由另一个变量唯一确定
- 当变量x 取某个值时,变量y 的取值对应着一个分布
- 各观测点分布在直线周围
11.1.2 相关关系的描述与测量
- 散点图:可以通过散点图判断两个变量之间有无相关关系,并对变量间的关系形态做出大致的描述。

- 相关系数:是度量变量之间线性关系强度的一个统计量。
- 若相关系数是根据总体全部数据计算的,称为总体相关系数,记为 ρ ρ ρ;
- 若是根据样本数据计算的,则称为样本相关系数,简称为相关系数,记为 r r r,也称为 Pearson \textbf{Pearson} Pearson相关系数或者线性相关系数。
- r = n ∑ x y − ∑ x ∑ y n ∑ x 2 − ( ∑ x ) 2 − n ∑ y 2 − ( ∑ y ) 2 r = \frac{n\sum{xy} - \sum{x}\sum{y}}{\sqrt{n\sum{x^2} - (\sum{x})^2} - \sqrt{n\sum{y^2} - (\sum{y})^2}} r=n∑x2−(∑x)2−n∑y2−(∑y)2n∑xy−∑x∑y
- 相关系数 r r r 的性质:
- r r r 的取值范围为 [ 0 , 1 ] [0,1] [0,1];
- y 和 x : { 完 全 负 线 性 相 关 关 系 , − 1 = r 负 线 性 相 关 关 系 , − 1 < r < 0 不 存 在 相 关 关 系 , r = 0 正 线 性 相 关 关 系 , 0 < r < 1 完 全 正 线 性 相 关 关 系 , r = 1 可 见 , 当 ∣ r ∣ = 1 是 y 的 取 值 完 全 依 赖 于 x , 二 者 为 函 数 关 系 。 ∣ r ∣ 越 趋 于 1 表 示 关 系 越 强 ; ∣ r ∣ 越 趋 于 0 表 示 关 系 越 弱 。 y和x: \begin{cases} 完全负线性相关关系 & ,-1 = r\\ 负线性相关关系 & ,-1 < r < 0 \\ 不存在相关关系 & ,\qquad\quad r = 0\\ 正线性相关关系 &,\quad 0 < r < 1 \\ 完全正线性相关关系 & ,\qquad\quad r = 1\\ \end{cases} \\ \qquad \\ 可见,当|r| = 1是y的取值完全依赖于x,二者为函数关系。\\ |r|越趋于1表示关系越强;|r|越趋于0表示关系越弱。 y和x:⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧完全负线性相关关系负线性相关关系不存在相关关系正线性相关关系完全正线性相关关系,−1=r,−1<r<0,r=0,0<r<1,r=1可见,当∣r∣=1是y的取值完全依赖于x,二者为函数关系。∣r∣越趋于1表示关系越强;∣r∣越趋于0表示关系越弱。
- r r r 具有对称性。即x与y之间的相关系数和y与x之间的相关系数相等,即 r x y = r y x r_{xy}= r_{yx} rxy=ryx
- r r r 数值大小与x和y原点及尺度无关,即改变x和y的数据原点及计量尺度,并不改变r数值大小
- r r r 仅仅是x与y之间线性关系的一个度量,它不能用于描述非线性关系。这意味着, r=0只表示两个变量之间不存在线性相关关系,并不说明变量之间没有任何关系
- r r r 虽然是两个变量之间线性关系的一个度量,却不一定意味着x与y一定有因果关系
- y 和 x 之 间 : { 不 相 关 , 0.3 < ∣ r ∣ 低 度 相 关 , 0.3 ≤ ∣ r ∣ < 0.5 中 度 相 关 , 0.5 ≤ ∣ r ∣ < 0.8 高 度 相 关 , ∣ r ∣ ≥ 0.8 上 述 解 释 必 须 建 立 在 对 相 关 系 数 的 显 著 性 进 行 检 验 的 基 础 之 上 。 y和x之间: \begin{cases} 不相关 & ,0.3<|r|\\ 低度相关 & ,0.3≤|r|<0.5 \\ 中度相关 & ,0.5≤|r|<0.8\\ 高度相关 & ,\qquad\;\; |r|≥0.8 \\ \end{cases} \\ \quad \\ 上述解释必须建立在对相关系数的显著性进行检验的基础之上。 y和x之间:⎩⎪⎪⎪⎨⎪⎪⎪⎧不相关低度相关中度相关高度相关,0.3<∣r∣,0.3≤∣r∣<0.5,0.5≤∣r∣<0.8,∣r∣≥0.8上述解释必须建立在对相关系数的显著性进行检验的基础之上。
11.1.3 相关关系的显著性检验
检验两个变量之间是否存在线性相关关系,通常将 r r r 作为 ρ ρ ρ 的估计值。
- r r r 的抽样分布(不写)
- r r r 的显著性检验
- 提出假设:
H 0 : ρ = 0 ; H 1 : ρ ≠ 1 ; \; H_0:ρ = 0;\\ H_1:ρ \ne 1; H0:ρ=0;H1:ρ=1; - 计算检验的统计量:
t = ∣ r ∣ n − 2 1 − t 2 ∼ t ( n − 2 ) t = |r|\sqrt{\frac{n-2}{1-t^2}} \sim t(n-2) t=∣r∣1−t2n−2∼t(n−2) - 进行决策:
- 根据给定的显著性水平 α \alpha α 和自由度 d f = n − 2 df = n-2 df=n−2查 t t t分布表,得出 t α / 2 ( n − 2 ) t_{\alpha/2}(n-2) tα/2(n−2)的临界值。
- 若 ∣ t ∣ > t α / 2 |t| > t_{\alpha/2} ∣t∣>tα/2,则拒绝 H 0 H_0 H0,表明总体的两个变量之间存在显著的线性关系;
- 提出假设:
11.2 一元线性回归的估计和检验
-
相关分析目的在于用相关系数测度变量之间的关系强度。
-
而回归分析侧重于考察变量之间的数量关系,并通过一定的数学表达式将这种关系描述出来,从而确定一个或几个变量(自变量)的变化对另一个特定变量(因变量)的影响程度。具体来说,回归分析具体解决以下几个方面的问题:
- 从一组样本数据出发,确定变量之间的数学关系式。
- 对这些关系式的可信程度进行各种统计检验,并从影响因变量的诸多变量中找出哪些变量的影响是显著的,哪些是不显著的。
- 利用所求的关系式,根据一个或几个自变量的取值来估计或预测因变量的取值,并给出这种估计或预测的可靠程度。
-
在回归分析中:
- 被预测或被解释的变量称为因变量,用y表示;
- 用来预测或被解释的一个或多个变量称为自变量,用x表示;
11.2.1 一元线性回归模型
涉及一个自变量的回归。
- 回归模型:描述因变量y 如何依赖于自变量x 和误差项 ε ε ε 的方程称为回归模型,一元线性回归模型可表示为:
y = β 0 + β 1 x + ε ( ε 是 被 称 为 误 差 项 的 随 机 变 量 , β 0 和 β 1 称 为 模 型 的 参 数 ) y = β_0 + β_1x + ε \\ (ε是被称为误差项的随机变量,β_0和β_1称为模型的参数) y=β0+β1x+ε(ε是被称为误差项的随机变量,β0和β1称为模型的参数)- 上述模型称为理论回归模型,对于这一模型,有以下几个假定:
- 因变量y与自变量x之间具有线性关系;
- 在重复抽样中,自变量x的取值是固定的,即假定x是非随机的;
- 对于满足:
- 正态性。 ε ∼ N ( 0 , σ 2 ) ε \sim N(0 , σ^2 ) ε∼N(0,σ2) 。对于所有的x 值, E ( y ) = β 0 + β 1 x E(y)=β_0+ β_1x E(y)=β0+β1x。
- 方差齐性。对于所有的x 值, D ( ε ) = σ 2 D(ε) = σ^2 D(ε)=σ2 , D ( y ) = σ 2 D(y) = σ^2 D(y)=σ2。
- 独立性。独立性意味着对于一个特定的x 值,它所对应的ε与其他x 值所对应的ε不相关;对于一个特定的x 值,它所对应的y值与其他x 所对应的y 值也不相关。
- 上述模型称为理论回归模型,对于这一模型,有以下几个假定:
- 回归方程 :描述因变量y的期望值如何依赖于自变量x的方程称为回归方程,一元线性回归方程的形式为:
E ( y ) = β 0 + β 1 x E(y) = β_0 + β_1x E(y)=β0+β1x- 一元线性回归方程的图示是一条直线,因此也被称为回归方程。
- β 0 β_0 β0是回归直线在y轴上的截距,是当x=0时y的期望值;
- β 1 β_1 β1是直线的斜率,它表示x每变动一个单位时,y的平均变动值;
- 估计的回归方程:如果 β 0 β_0 β0和 β 1 β_1 β1未知,则用样本统计量 β ^ 1 \hatβ_1 β^1和 β ^ 1 \hatβ_1 β^1代替回归方程中的未知参数 β 0 β_0 β0和 β 1 β_1 β1来计算y的期望值,就得到了估计的回归方程:
y ^ = β ^ 0 + β ^ 1 x \hat y = \hatβ_0 + \hatβ_1x y^=β^0+β^1x- β ^ 0 \hatβ_0 β^0是回归直线在y轴上的截距,是当x=0时y的期望值;
- β ^ 1 \hatβ_1 β^1是直线的斜率,它表示x每变动一个单位时,y的平均变动值;
11.2.2 参数的最小二乘估计
- 最小二乘法:使因变量的观察值与估计值之间的误差平方和达到最小来求得 β ^ 1 \hatβ_1 β^1和 β ^ 1 \hatβ_1 β^1的方法:
∑ ( y i − y ^ i ) 2 = ∑ ( y i − β ^ 0 − β ^ 1 x i ) 2 最 小 \sum{(y_i - \hat y_i)}^2 = \sum{(y_i - \hat β_0 - \hatβ_1x_i)^2}最小 ∑(yi−y^i)2=∑(yi−β^0−β^1xi)2最小

- 用最小二乘法拟合的直线来代表x与y之间的关系与实际数据的误差比其他任何直线都小
- 根据最小二乘法,可得求解 β ^ 1 \hatβ_1 β^1和 β ^ 1 \hatβ_1 β^1的公式如下:
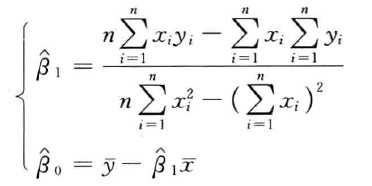
11.2.3 回归直线的拟合优度
估计或预测的精度如何,将取决于回归直线对观测数据的拟合程度。各观测点越是紧密围绕直线,说明对观测数据的拟合程度越好,反之越差。
- 判定系数:判定系数是对估计的回归方程拟合优度的度量,也称为决定系数。
- 变差:因变量y 的取值是不同的,y 取值的这种波动,可用 ( y − y ^ ) − ( y − y ˉ ) (y-\hat y) - (y - \bar y) (y−y^)−(y−yˉ)也就是 y − y ˉ y - \bar y y−yˉ来表示;

- 总平方和( S S T SST SST):反映因变量的n 个观察值与其均值的总误差。
S S T = ∑ ( y i − y ˉ ) 2 SST = \sum{(y_i - \bar y)^2} SST=∑(yi−yˉ)2 - 残差平方和:又称误差平方和,反映除x 以外的其他因素对y 取值的影响,也称为不可解释的平方和或剩余平方和。
S S E = ∑ ( y i − y ^ ) 2 SSE = \sum{(y_i - \hat y)^2} SSE=∑(yi−y^)2 - 回归平方和(SSR):反映自变量x 的变化对因变量y 取值变化的影响,或者说,是由于x 与y 之间的线性关系引起的y 的取值变化,也称为可解释的平方和。
S S R = ∑ ( y ^ − y ˉ ) 2 SSR = \sum{(\hat y - \bar y)^2} SSR=∑(y^−yˉ)2 - 三者的关系为:
S S T = S S E + S S R SST = SSE + SSR SST=SSE+SSR - 判定系数( R 2 R^2 R2):回归平方和占总误差平方和的比例
R 2 = S S R S S T = S S R S S R + S S E = 1 − S S E S S T R^2 = \frac{SSR}{SST} = \frac{SSR}{SSR+SSE} = 1 - \frac{SSE}{SST} R2=SSTSSR=SSR+SSESSR=1−SSTSSE- 反映回归直线的拟合程度;
- 取值范围在 [ 0 , 1 ] [ 0 , 1 ] [0,1]之间;
- R 2 → 1 R^2 →1 R2→1,说明回归方程拟合的越好; R 2 → 0 R^2→0 R2→0,说明回归方程拟合的越差;
- 判定系数平方根等于相关系数;
- 变差:因变量y 的取值是不同的,y 取值的这种波动,可用 ( y − y ^ ) − ( y − y ˉ ) (y-\hat y) - (y - \bar y) (y−y^)−(y−yˉ)也就是 y − y ˉ y - \bar y y−yˉ来表示;
- 估计标准误差( s e s_e se):反映实际观察值在回归直线周围的分散状况,是均方残差(MSE)的平方根
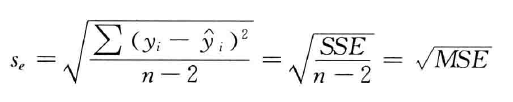
11.2.4 显著性检验
线性关系的检验:
- 提出假设:
H 0 : β 1 = 0 两 个 变 量 之 间 的 线 性 关 系 不 显 著 H_0: \beta_1 = 0 \qquad 两个变量之间的线性关系不显著 H0:β1=0两个变量之间的线性关系不显著 - 计算检验统计量F:
F = S S R / 1 S S E / ( n − 2 ) = M S R M S E ∼ F ( 1 , n − 2 ) F = \frac{SSR/1}{SSE/(n-2)} = \frac{MSR}{MSE} \sim F(1, n-2) F=SSE/(n−2)SSR/1=MSEMSR∼F(1,n−2) - 确定显著性水平α
- 作出决策:
- 用F分布:查找临界值 F α ( 1 , n − 2 ) F_{\alpha}(1, n-2) Fα(1,n−2)在 F F F分布表中的值
- F > F α F > F_\alpha F>Fα,拒绝 H 0 H_0 H0,表明两个变量之间的线性关系是显著的。
- F < F α F < F_\alpha F<Fα,不拒绝 H 0 H_0 H0,没有证据表明两个变量之间的线性关系显著。
- 用P值:
- 若 P < α P < α P<α,拒绝 H 0 H_0 H0,表明两个变量之间的线性关系显著
- 若 P > α P > α P>α,不拒绝 H 0 H_0 H0,没有证据表明两个变量之间的线性关系显著。
- 用F分布:查找临界值 F α ( 1 , n − 2 ) F_{\alpha}(1, n-2) Fα(1,n−2)在 F F F分布表中的值
回归系数的检验:
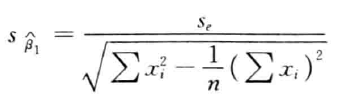
- 提出假设:
H 0 : β 1 = 0 两 个 变 量 之 间 的 线 性 关 系 不 显 著 H 1 : β 1 ≠ 0 两 个 变 量 之 间 的 线 性 关 系 显 著 H_0: \beta_1 = 0 \qquad 两个变量之间的线性关系不显著\\ H_1: \beta_1 \ne 0 \qquad\quad 两个变量之间的线性关系显著 H0:β1=0两个变量之间的线性关系不显著H1:β1=0两个变量之间的线性关系显著 - 计算检验统计量t:
t = β ^ 1 s β ^ 1 ∼ t ( n − 2 ) t = \frac{\hat \beta_1}{s_{\hat \beta_1}}\sim t(n-2) t=sβ^1β^1∼t(n−2) - 确定显著性水平α
- 作出决策:
- 用F分布:查找临界值 t α / 2 ( n − 2 ) t_{\alpha/2}(n-2) tα/2(n−2)在 F F F分布表中的值
- t > t α / 2 t > t_{\alpha/2} t>tα/2,拒绝 H 0 H_0 H0,回归系数等于0的可能性小于 α \alpha α,表明两个变量之间的线性关系是显著的。
- t < t α / 2 t < t_{\alpha/2} t<tα/2,不拒绝 H 0 H_0 H0,没有证据表明两个变量之间的线性关系显著。
- 用P值:
- 若 P < α P < α P<α,拒绝 H 0 H_0 H0,表明两个变量之间的线性关系是显著的。
- 若 P > α P > α P>α,不拒绝 H 0 H_0 H0,二者不存在显著的线性关系。
- 用F分布:查找临界值 t α / 2 ( n − 2 ) t_{\alpha/2}(n-2) tα/2(n−2)在 F F F分布表中的值
11.3 利用回归方程进行预测
11.3.1 平均值的置信区间
- 置信区间(confidence interval):利用估计的回归方程,对于自变量x 的一个给定值 x 0 x_0 x0 ,求出因变量 y y y的平均值的估计区间,这一估计区间称为置信区间。

11.3.2 个别值的预测区间
- 预测区间(prediction interval):利用估计的回归方程,对于自变量x 的一个给定值x0 ,求出因变量y 的一个个别值的估计区间,这一区间称为预测区间。
比平均值的公式根号内多了个1而已:

11.4 残差分析
11.4.1 残差与残差图(检验方差齐性)
- 残差:因变量的观测值与根据估计的回归方程求出的预测值之差,用 e e e表示,反映了用估计的回归方程去预测而引起的误差。
- 第i个观测值的残差写为:
e i = y i − y ^ i e_i = y_i - \hat y_i ei=yi−y^i - 可用于确定有关误差项ε的假定是否成立
- 用于检测有影响的观测值

- 第i个观测值的残差写为:
11.4.2 标准化残差(检验正态性)
- 标准化残差:也称为Pearson 残差或半学生化残差(semistudentized
residuals)。- 第i个观察值的标准化残差写为:
z e i = e i s e = y i − y ^ i s e s e 是 残 差 的 标 准 差 的 估 计 。 z_{e_i} = \frac{e_i}{s_e} = \frac{y_i - \hat y_i}{s_e} \qquad s_e是残差的标准差的估计。 zei=seei=seyi−y^ise是残差的标准差的估计。 - 用以直观地判断误差项服从正态分布这一假定是否成立
- 若假定成立,标准化残差的分布也应服从正态分布,因此在标准化残差图中,大约有95%的标准化残差在-2到+2之间
- 第i个观察值的标准化残差写为: