学习进行到此处,发现程序性能越来越差,本书竟然没提到傅立叶变化还有快速变化改进方法。下边我就介绍下快速变换的原理以及程序实现。
1、FFT的由来
离散傅里叶变换(Discrete Fourier Transform,DFT)是数字信号处理最重要的基石之一,也是对信号进行分析和处理时最常用的工具之一。在200多年前法国数学家、物理学家傅里叶提出后来以他名字命名的傅里叶级数之后,用DFT这个工具来分析信号就已经为人们所知。历史上最伟大的数学家之一。
欧拉是第一个使用“函数”一词来描述包含各种参数的表达式的人,例如:y = f(x)。他是把微积分应用于物理学的先驱者之一。 给出了一个用实变量函数表示傅立叶级数系数的方程; 用三角级数来描述离散声音在弹性媒介中传播,发现某些函数可以通过余弦函数之和来表达。 但在很长时间内,这种分析方法并没有引起更多的重视,最主要的原因在于这种方法运算量比较大。直到1965年,Cooley和Tukey在《计算机科学 》发表著名的《机器计算傅立叶级数的一种算法》论文,FFT才开始大规模应用。
那个年代,有个肯尼迪总统科学咨询委员会。其中有项研究主题是,对苏联核测试进行检测,Tukey就是其中一员。美国/苏联核测试提案的批准,主要取决于不实地访问核测试设施而做出检测的方法的发展。其中一个想法是,分析离海岸的地震计情况,这种计算需要快速算法来计算DFT。其它应用是国家安全,如用声学探测远距离的核潜艇。所以在军事上,迫切需要一种快速的傅立叶变换算法,这也促进了FFT的正式提出。
FFT的这种方法充分利用了DFT运算中的对称性和周期性,从而将DFT运算量从N2减少到N*log2N。当N比较小时,FFT优势并不明显。但当N大于32开始,点数越大,FFT对运算量的改善越明显。比如当N为1024时,FFT的运算效率比DFT提高了100倍。在库利和图基提出的FFT算法中,其基本原理是先将一个N点时域序列的DFT分解为N个1点序列的DFT,然后将这样计算出来的N个1点序列DFT的结果进行组合,得到最初的N点时域序列的DFT值。实际上,这种基本的思想很早就由德国伟大的数学家高斯提出过,在某种情况下,天文学计算(也是现在FFT应用的领域之一)与等距观察的有限集中的行星轨道的内插值有关。由于当时计算都是靠手工,所以产生一种快速算法的迫切需要。 而且,更少的计算量同时也代表着错误的机会更少,正确性更高。高斯发现,一个富氏级数有宽度N=N1*N2,可以分成几个部分。计算N2子样本DFT的N1长度和N1子样本DFT的N2长度。只是由于当时尚欠东风——计算机还没发明。在20世纪60年代,伴随着计算机的发展和成熟,库利和图基的成果掀起了数字信号处理的革命,因而FFT发明者的桂冠才落在他们头上。
之后,桑德(G.Sand)-图基等快速算法相继出现,几经改进,很快形成了一套高效运算方法,这就是现在的快速傅立叶变换(FFT)。这种算法使DFT的运算效率提高1到2个数量级,为数字信号处理技术应用于各种信号的实时处理创造了良好的条件,大大推进了数学信号处理技术。1984年,法国的杜哈梅(P.Dohamel)和霍尔曼(H.Hollamann)提出的分裂基块快速算法,使运算效率进一步提高。
库利和图基的FFT算法的最基本运算为蝶形运算,每个蝶形运算包括两个输入点,因而也称为基-2算法。在这之后,又有一些新的算法,进一步提高了FFT的运算效率,比如基-4算法,分裂基算法等。这些新算法对FFT运算效率的提高一般在50%以内,远远不如FFT对DFT运算的提高幅度。从这个意义上说,FFT算法是里程碑式的。可以说,正是计算机技术的发展和FFT的出现,才使得数字信号处理迎来了一个崭新的时代。除了运算效率的大幅度提高外,FFT还大大降低了DFT运算带来的累计量化误差,这点常为人们所忽略。
2、直接计算DFT的问题及改进路径
2.1 问题的提出
设有限长序列x(n),非零值长度为N,若对x(n)进行一次DFT运行,共需要多大的运算工作量。
2.2 DFT的运算量
DFT和IDFT的变换式:
注意:
由上面的结算可得DFT的计算量如下:

复数乘法的计算量:(a+jb)(c+jd)=(ab-bd)+j(bc+ad)
下面通过两个实例来说明计算量:
例一:计算一个N点DFT,共需次复乘。以做一次复乘1计算,若N=4096,所需时间为
![]()
例二:石油勘探,有24个通道的记录,每通道波形记录长度为5秒,若每秒抽样500点/秒。
1. 每道总抽样点数:500*5 = 2500点。
2. 24道总抽样点数:24*2500=6万点。
3. DFT复乘运算时间:![]()
![]()
由于计算量大,且要求相当大的内存,难以实现实时处理,限制了DFT的应用,人们一直在寻求一种能提高DFT运算速度的方法。
FFT便是Cooley和Tukey在1995年提出来的快速算法,它可以使运算速度提高几百倍,从而使数字信号处理成为一个新兴的应用学科。
3、 改善DFT运算效率的基本途径
1、利用DFT运算的系数![]() 的固有对称性和周期性,改善DFT的运算效率。
的固有对称性和周期性,改善DFT的运算效率。
1)对称性
2)周期性
3)可约性

2、将长序列DFT利用对称性和周期性分解为短序列DFT的思路
因为DFT的运算量与N2成正比,如果一个大点数N的DFT能分解为若干小点数DFT的组合,则显然可以达到减少运算工作量的效果。

FFT算法的基本思想:
Ø 利用DFT系数的特性,合并DFT运算中的某些项。
Ø 把长序列DFTà短序列DFT,从而减少运算量。
FFT算法分类:
时间抽选法
DIT: Decimation-In-Time
频率抽选法
DIF: Decimation-In-Frequency
4 按时间抽选的基2-FFT算法
4.1 算法原理
设输入序列长![]() 度为(M为正整数),将该序列按时间顺序的奇偶分解为越来越短的子序列,称为基2按时间抽取的FFT算法。也称为Coolkey-Tukey算法。
度为(M为正整数),将该序列按时间顺序的奇偶分解为越来越短的子序列,称为基2按时间抽取的FFT算法。也称为Coolkey-Tukey算法。
其中基2表示:![]() ,M为整数。若不满足这个条件,可以人为地加上若干零值(加零补长)使其达到
,M为整数。若不满足这个条件,可以人为地加上若干零值(加零补长)使其达到![]() 。
。
4.2 算法步骤
Ø 分组,变量置换

先将x(n)按n的奇偶分为两组,作变量置换:
当n = 偶数时,令n = 2r;
当n = 奇数时,令n = 2r+1;
得到:
x(2r)=x1(r)
x(2r+1)=x2(r) r = 0,……-1
Ø 分组,变量置换
其中k = 0, 1,…. N/2 – 1。到此时为止,似乎没什么用,不过是拆成2部分算,计算量其实是一样的。那么我们再利用系数![]() 的周期特性来看看。
的周期特性来看看。
又考虑到![]() 的对称性:
的对称性:

有了上面的计算结果后。我们可以看出,只要算出X1,X2和Wnk的值,就可以一次算出2个数,即X(K)和X(N/2+K)的值,这不就优化了吗?
我们可以得到如下的蝶形运算流图符号:

关于这个蝶形运算流图符号说明如下:
1. 1个蝶形运算需要1次复乘,2次复加。
2. 左边两路为输入。
3. 右边两路为输出。
4. 中间以一个小圆表示加减运算(右上路为相加输出,右下路为相减输出)。
分解后的运算量

运算量减少了近一半。
例子:求![]() 点FFT变化。按N=8àN/2=4,做4点的DFT,先将N=8点的DFT分解成2个4点的DFT:
点FFT变化。按N=8àN/2=4,做4点的DFT,先将N=8点的DFT分解成2个4点的DFT:
可知: 时域上 x(0),x(2),x(4),x(6)为偶子序列。
x(1),x(3),x(5),x(7)为奇子序列。
频域上 X(0) 到X(3) 由X(k)给出
X(4) 到X(7) 由X(k+N/2)给出
N=8点的直接DFT的计算量为:

得到![]() 和
和![]() 需要:
需要:

此外,还有4个蝶形结,每个蝶形结需要1次复乘,2次复加。一共是:复乘4次,复加8次。
用分解的方法的得到X(k)需要:
复乘:32+4=36次
复加:24+8=32次
![]() 按时间抽取的DFT分解过程:
按时间抽取的DFT分解过程:

因为4点DFT还是比较麻烦,所以再继续分解。
若将N/2(4点)子序列按奇/偶分解成两个N/4点(2点)子序列。即对将x1(r)和x2(r)分解成奇、偶两个N/4点(2点)的子序列。

那么,


因此可以对两个N/2点的DFT再分别作进一步的分解。将一个8点的DFT可以分解成四个2点的DFT,直到最后得到两两点的DFT为止。
由于这种方法每一步分解都是按输入序列是属于偶数还是奇数来抽取的,所以称为“按时间抽取的FFT算法”。
下图是由4个两点DFT组成的8点DFT:

下图是按8点抽取的FFT运算流图(就是最后一级了,那就是一个数的DFT,不就等于自己嘛):

这里注意观察蝶形图的系数
第一级:Wn4 (n=0)
第二级:Wn2 (n=1,2)
第三级:Wn1 (n=1,2,3,4)
5、IDFT的快速变换
FFT后如何变换回来呢,按照公式,1/N看成一个常量,和DFT区别是Wn(-nk)。其他一样
到此理论结束,下边开始编写程序。
1、首先观察上一个图,是通过一级一级的推算,最后得到X的,所以第一步是先初始化最左边的序列。这个楼主没什么好方法,是常规的移动位置完成
2、计算每个级组个数,定位每组的上半部分,因为下半是可以相减计算的,第一级1个,第二级是2个。。。
3、计算每个级别![]() 的k值
的k值
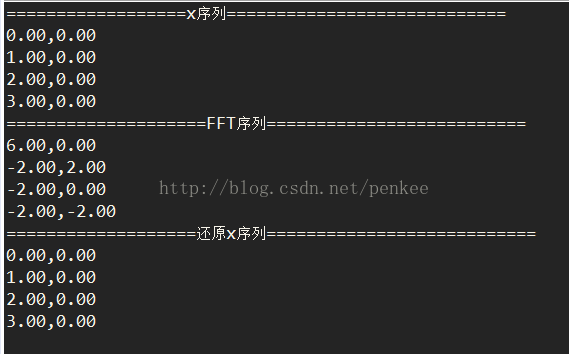
详情见
https://github.com/penkee/imagecal/blob/master/app-dao/src/test/java/com/dcloud/app_dao/TestFFT.java
那么二维的FFT如何实现呢?下回研究
6、二维离散FFT
通过转换,将F1看成是一维变换,y相当于上文的n。v相当于k。x是常量。那么就简化为M个x的一维FFT计算。
下边继续看,将v看成常量,即f1(x)=F1(x,v)。 那么发现其实最后变换又是一个FFT,u相当于上文的k。x相当于n