最近复习了下最短路,顺便写篇博客加强下自己的印象
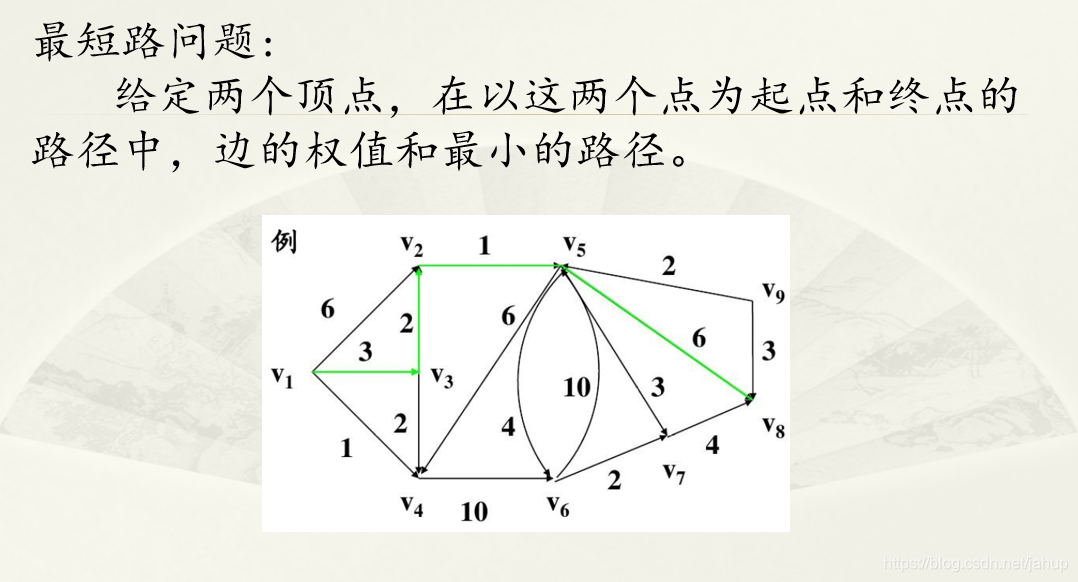
1.Floyd算法
我认为是最短路最简单的算法,但一般来说简单的都不是什么好东西,因为复杂度比较高;
*核心思想:
要缩短两点之间的距离,就需要第三个顶点来松弛。
*具体步骤:
依次用1到n号顶点做中转,松弛任意两点之间的距离。
因为这个算法比较简单,就直接上代码了;
#include<iostream>
using namespace std;
const int N=2000;
int main()
{
int maps[N][N];
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
{
if(i==j)
maps[i][j]=0;//起点和终点相同,路程为0
else
maps[i][j]=INT_MAX;//一开始没有路,则全部是无穷大
}
int n,m;//假设有n条路,m个城市
cin>>n;
int a,b,c;
for(int i=1;i<=n;i++)
{
cin>>a>>b>>c;
maps[a][b]=c;
maps[b][a]=c;//假设是双向路
}
for(int i=1;i<=m;i++)//枚举用来松弛的点
for(int j=1;j<=m;j++)
for(int k=1;k<=m;k++)
{
if(maps[j][k]<maps[j][i]+maps[i][k]);//通过该点松弛后距离变小了
maps[j][k]=maps[j][i]+maps[i][k];
}
cout<<maps[][]<<endl;//求得任意2点间的最短路
}
时间复杂度(o(m^3))
可以说对于百分之90的题 这个算法都是过不了的
2.Dijkstra算法
这个算法还是比较常用的,一定要掌握
*核心思想:
通过“边”来松弛源点顶点到其余个顶点的路程
*具体步骤:
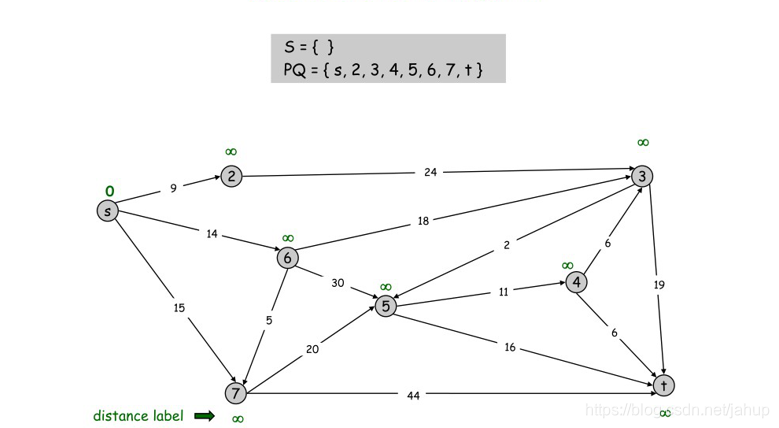
假设s是起点
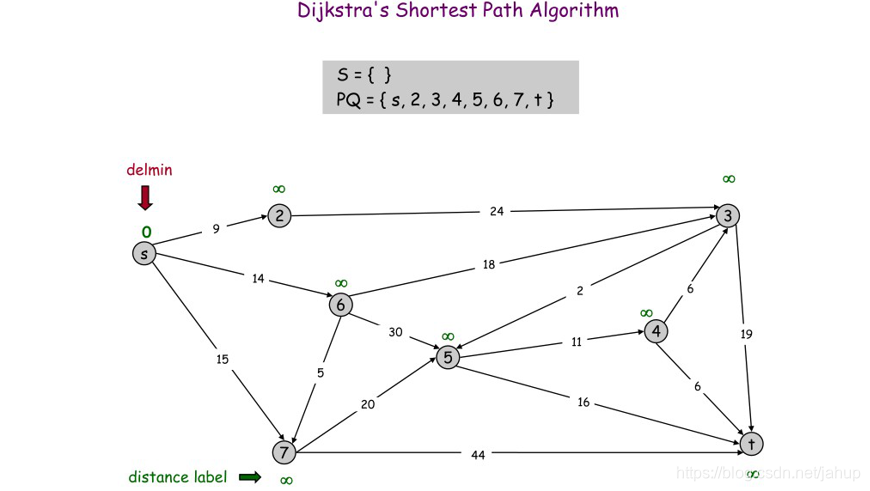
寻找s集合到PQ集合最短的边
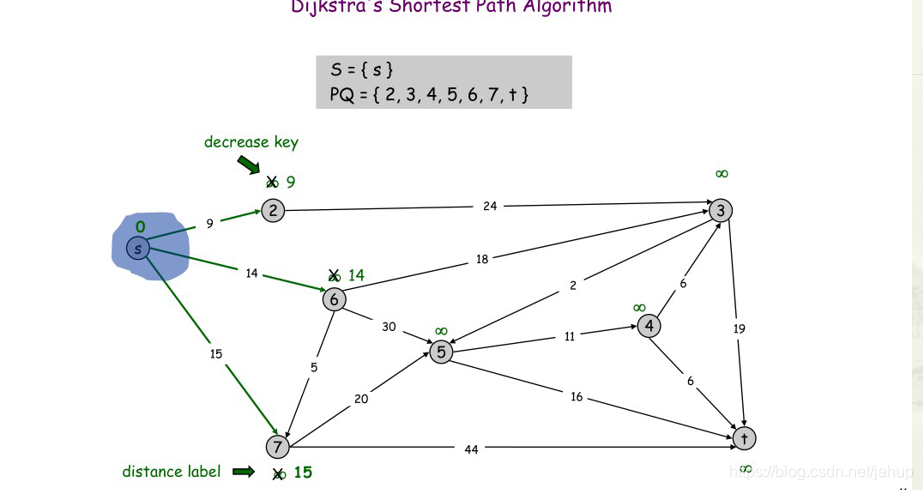
到2点的距离是最短的
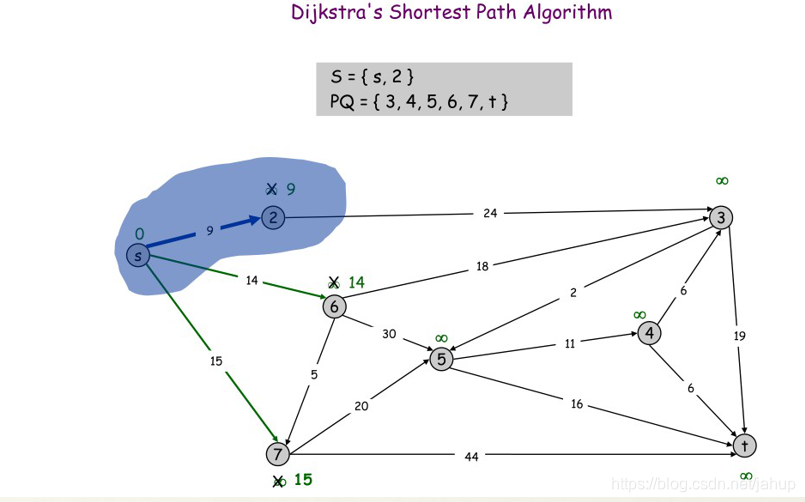
接下来到6的距离是最短的
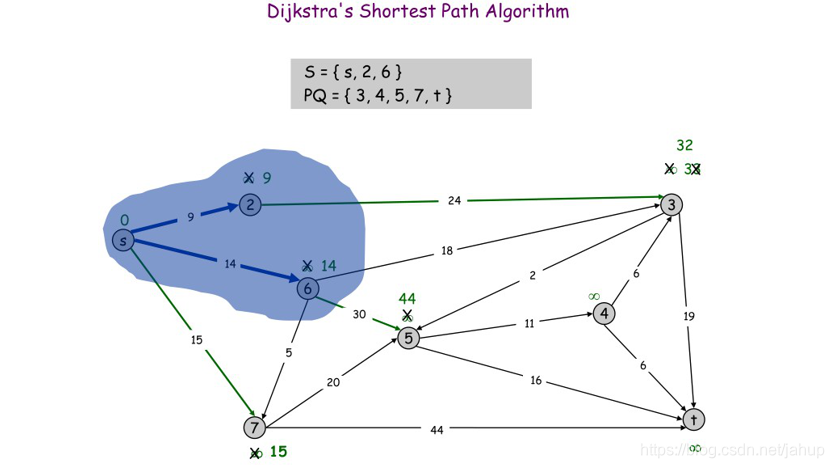
然后是7号点
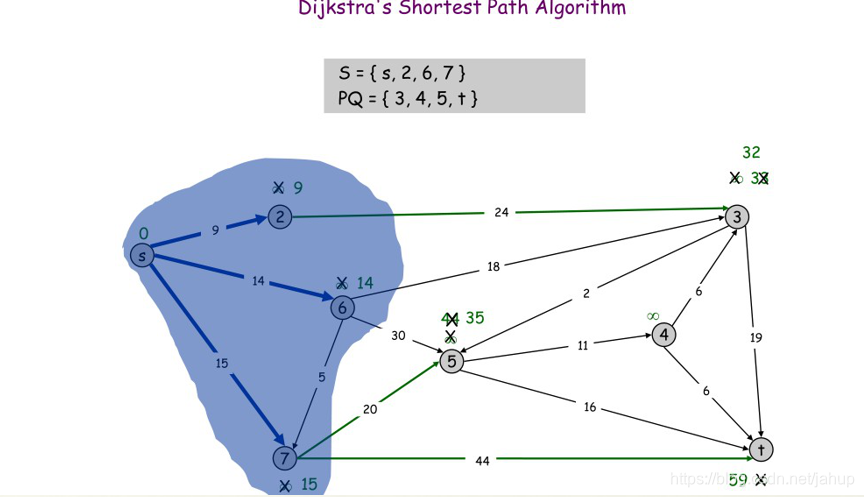
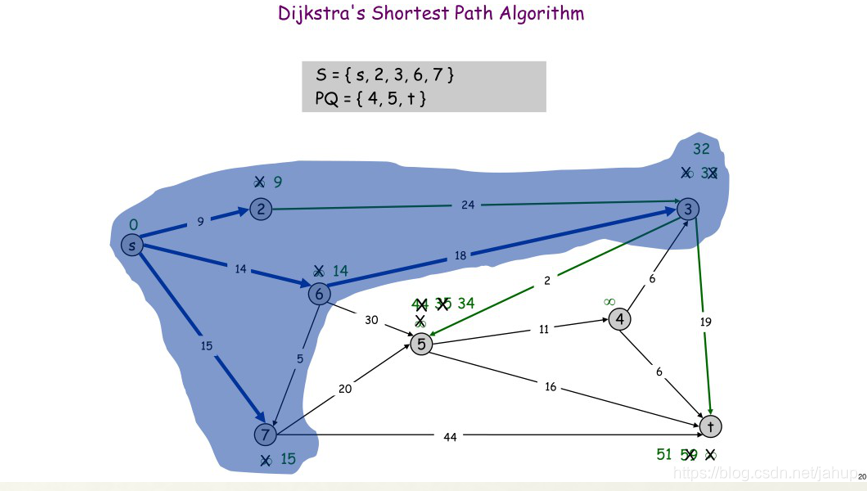
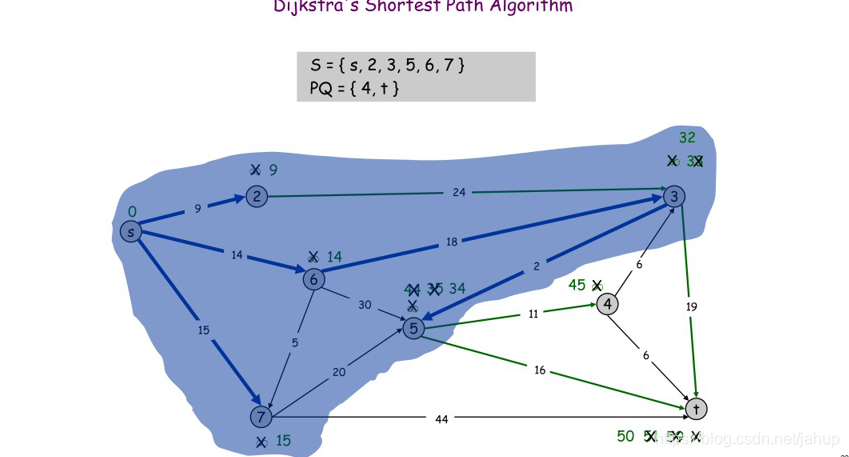
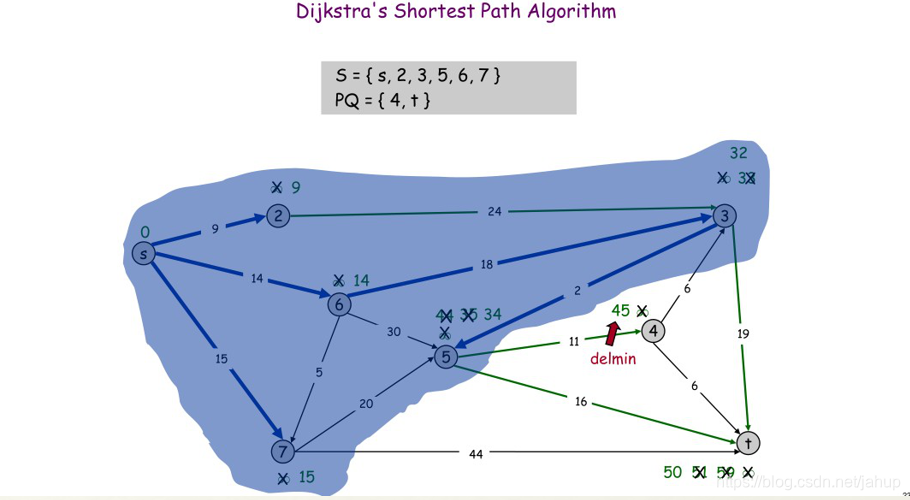
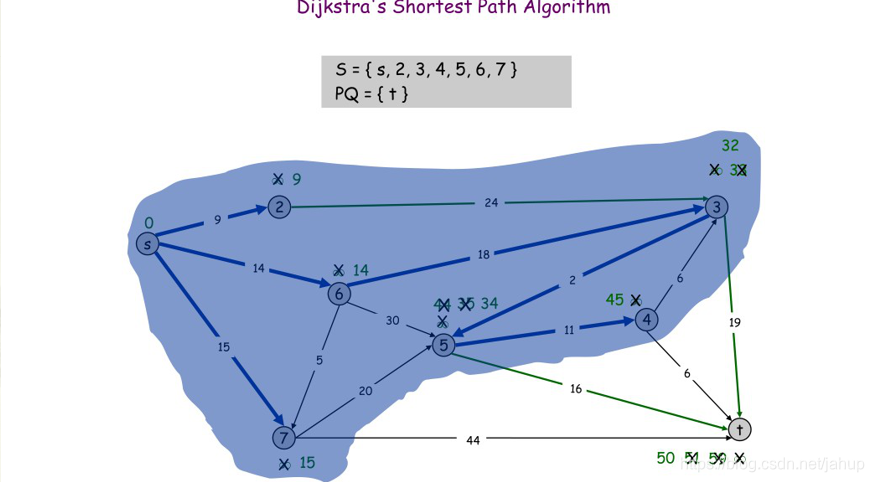
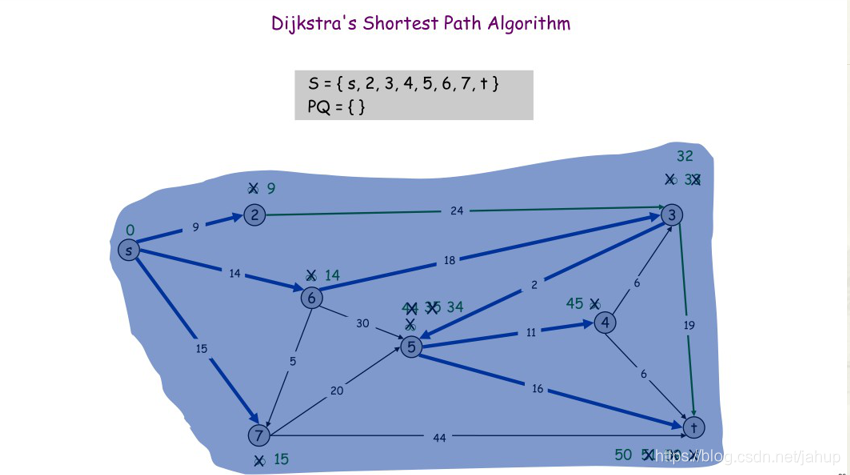
(图片是学长那偷的)
这样s点到所有点的最短路就找出来了,我们来看看代码怎么写;(记住核心思想:通过“边”来松弛源点顶点到其余个顶点的路程)
#include<cstdio>
#include<queue>
#include<vector>
#include<iostream>
#define inf 0x3f3f3f
const int maxn=1005;
using namespace std;
typedef pair<int,int> P; //前面放到 dis[i],后面放i
struct node{
int v,w;
}E;
vector<node> edge[maxn];
int dis[maxn];
int main(){
int n,m;
int u;
while(scanf("%d%d",&n,&m),n){
//初始化
for(int i=1;i<=n;i++){
dis[i]=inf;
}
//存图
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&E.v,&E.w);
edge[u].push_back(E);
}
priority_queue <P,vector<P>,greater<P> > que;
while(!que.empty()) que.pop();
dis[1]=0;
que.push(P(dis[1],1));
while(!que.empty()){
P now=que.top(); que.pop();
int nowu=now.second;
for(int i=0;i<edge[nowu].size();i++){
E=edge[nowu][i];
if(dis[E.v]>dis[nowu]+E.w){
dis[E.v]=dis[nowu]+E.w;
que.push(P(dis[E.v],E.v));
}
}
}
for(int i=1;i<=n;i++)
printf("%d ",dis[i]);
printf("\n");
}
return 0;
}
/*
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
*/
我这里写的是优先队列优化的版本时间复杂度为O((m+n)logn),但这个算法存在一定的弊端,它无法解决带有负权边的问题,为什么了,假设有一个回路,权值之和为负数,那么我们反复走这个回路,花费可以趋近负无穷
3.Bellman-Ford(解决负权边单源最短路)(边是带方向的)
核心思路:
对所有的边进行n-1次松弛操作。Bellmam-Ford第k轮松弛操作其实是源点“最多经过k条边”到达其余各个顶点的最短路径。所以虽最多进行n-1次松弛操作。
基本步骤:
n-1次松弛中,反复遍历所有的边,来缩短起点到其他点的距离
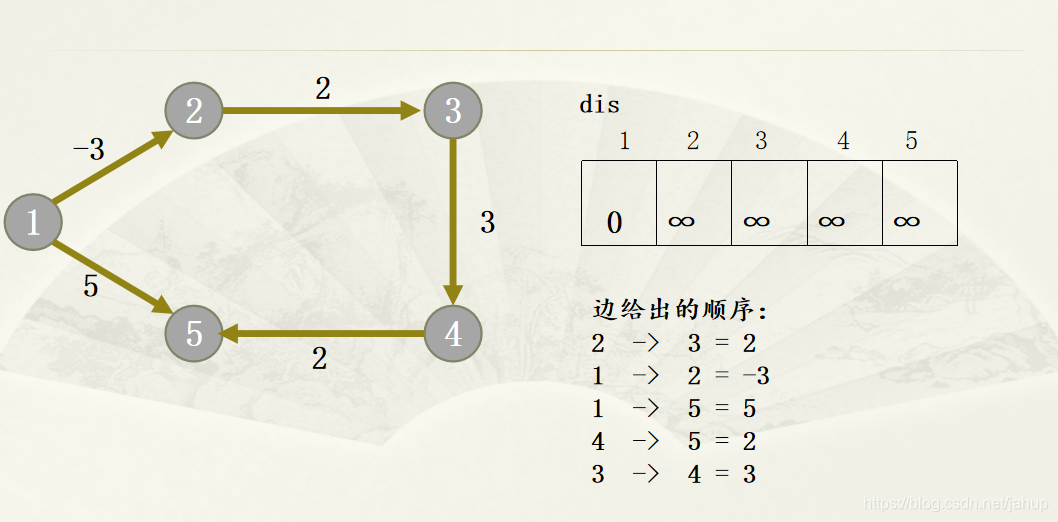
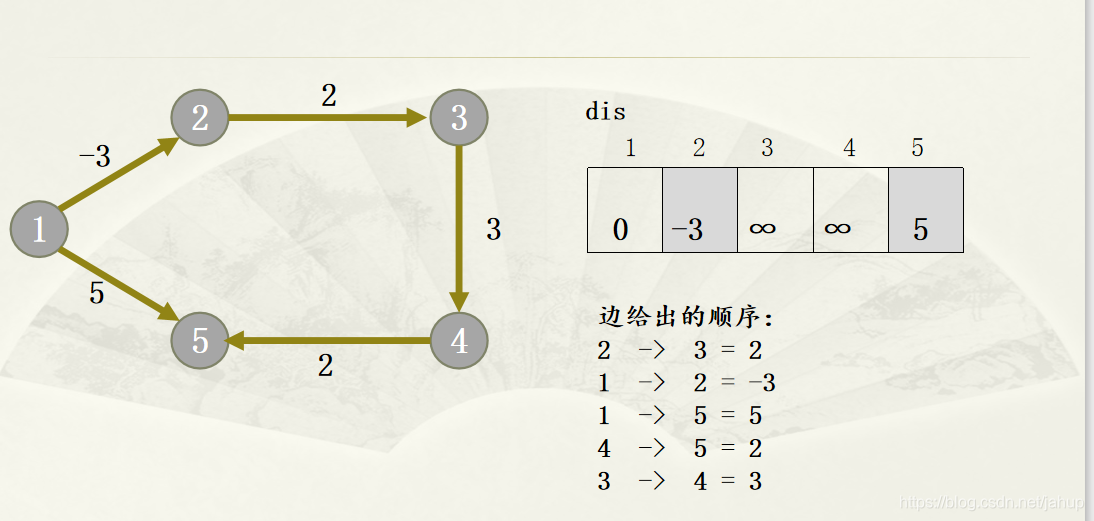
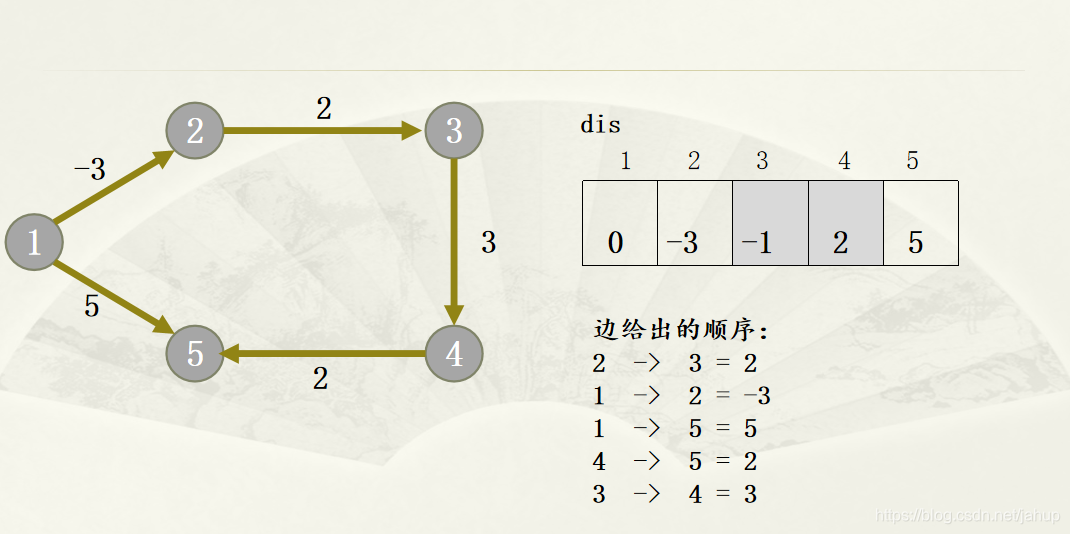
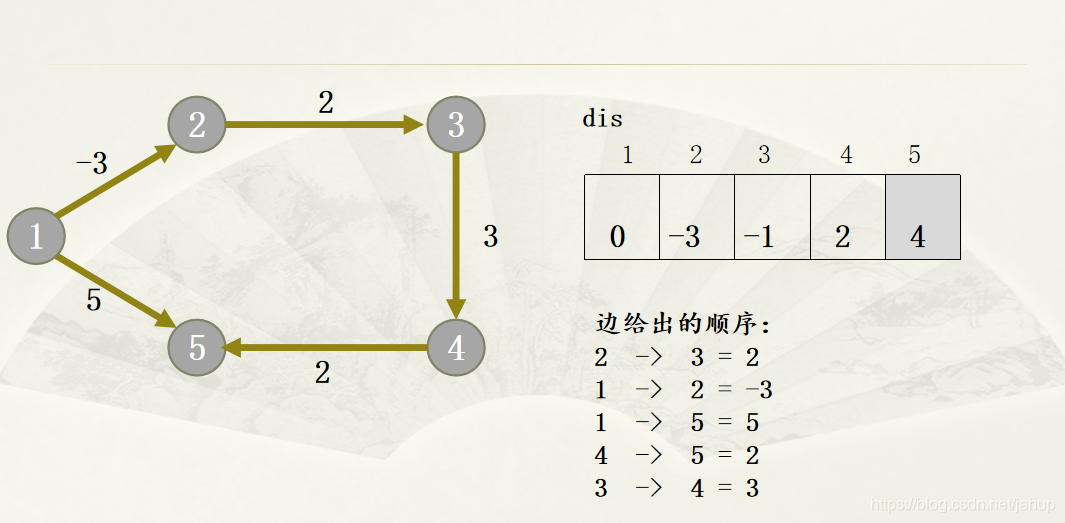
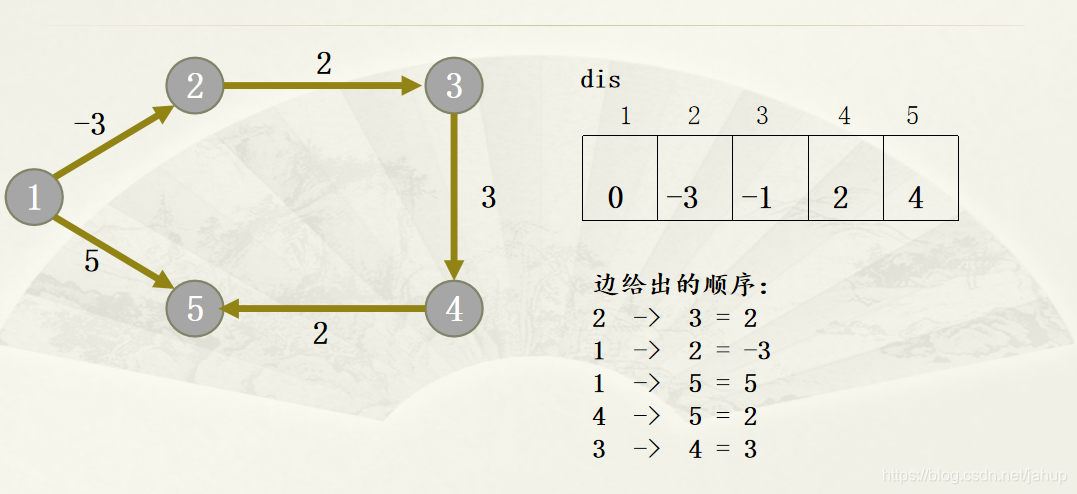
优化:
在实际操作中,通常在未达到n-1轮松弛前就已经计算出了最短路,我们可以用check标记一下dis数组在某轮操作中是否发生了变化,如果没有变化,便跳出循环即可。
#include<cstdio>
#include<vector>
#include<iostream>
#define inf 0x3f3f3f
const int maxn=1005;
using namespace std;
int dis[maxn];
int u[maxn],v[maxn],w[maxn];
int main(){
int n,m,check;
while(scanf("%d%d",&n,&m),n,m){
//存图
for(int i=1;i<=m;i++)
scanf("%d%d%d",&u[i],&v[i],&w[i]);
//初始化dis数组
for(int i=1;i<=n;i++)
dis[i]=inf;
dis[1]=0;
//进行n-1轮松弛
for(int k=1;k<=n-1;k++){
check=0;
//遍历每一条边
for(int i=1;i<=m;i++){
if(dis[v[i]]>dis[u[i]]+w[i]){
dis[v[i]]=dis[u[i]]+w[i];
check=1;
}
}
if(check==0) break;
}
for(int i=1;i<=n;i++)
printf("%d ",dis[i]);
printf("\n");
/*
//判断是否有负权回路
int flag=0;
for(int i=1;i<=m;i++)
if(dis[v[i]]>dis[u[i]]+w[i]) flag=1;
if(flag==0) printf("no\n");
else printf("yes\n");
*/
}
return 0;
}
/*
5 5
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
*/
(再次感谢学长学姐们的图)