- 前言: …
-
目录
1 Introdution
1.1 Time Analysis
- Computation time distribution of individual layers, on both GPUs and CPUs for the forward pass.

- It shows the computation time distribution of individual layers on both GPUs and CPUs for the forward pass. The backward pass distribution is similar so they are omitted here.
It could be observed that both platforms spend most computation time on dense convolution and fully connected layers, but the GPU is better capable of handling layers that are memory-bounded, such as pooling and normalization, possibly due to the high memory bandwidth inside the GPU.
它显示了GPU和CPU上用于前向传递的各个层的计算时间分布。 反向传递分布相似,因此在此省略。
可以观察到,两个平台在卷积和全连接层上花费了最多的计算时间,
但是GPU能够更好地处理受内存限制的层,例如池化和归一化,这可能是因为GPU内的高内存带宽 。
1.2 Conv Calculation
- There are many ways to calculate the convolution. Common methods are as follows: Sliding window, Im2col, FFT, Winograd…
- 计算卷积的方法有很多种,常见的有以下几种方法:
滑窗:这种方法是最直观最简单的方法。 但是,该方法不容易实现大规模加速,因此,通常情况下不采用这种方法(但是也不是绝对不会用,在一些特定的条件下该方法反而是最高效的)。
im2col:目前几乎所有的主流计算框架包括 Caffe, MXNet 等都实现了该方法. 该方法把整个卷积过程转化成了GEMM过程,而GEMM在各种 BLAS 库中都是被极致优化的,一般来说,速度较快。
BLAS(Basic Linear Algebra Subprograms)是一组线性代数计算中通用的基本运算操作函数集合[1] 。BLAS库中函数根据运算对象的不同,分为3个level。Level 1 函数处理单一向量的线性运算以及两个向量的二元运算。Level 2 函数处理 矩阵与向量的运算,同时也包含线性方程求解计算。Level 3 函数包含矩阵与矩阵运算。GEMM在深度学习中是十分重要的,全连接层以及卷积层基本上都是通过GEMM来实现的,而网络中大约90%的运算都是在这两层中。而一个良好的GEMM的实现可以充分利用系统的多级存储结构和程序执行的局部性来充分加速运算。GEMM矩阵乘积操作。
FFT:傅里叶变换和快速傅里叶变化是在经典图像处理里面经常使用的计算方法,但是,在 ConvNet中通常不采用,主要是因为在 ConvNet 中的卷积模板通常都比较小,例如 3×3 等,这种情况下,FFT 的时间开销反而更大,所以很少在CNN中利用FFT实现卷积。
Winograd: Winograd 是存在已久最近又被重新发现的方法,在大部分场景中, Winograd方法都显示较大的优势,目前cudnn中计算卷积就使用了该方法。
1.3 im2col
-
a

b

图示:图a,卷积基本操作,仅仅是单通道,多通道类似;
卷积就是卷积核跟图像矩阵的运算。卷积核是一个小窗口,记录的是权重。卷积核在输入图像上按步长滑动,每次操作卷积核对应区域的输入图像,将卷积核中的权值和对应的输入图像的值相乘再相加,赋给卷积核中心所对应的输出特征图的一个值,如图所示。
图b,以上我们已经知道了卷积是如何操作的,im2col的作用就是优化卷积运算,如何优化呢,我们先学习一下这个函数的原理。
我们假设卷积核的尺寸为 2x2,输入图像尺寸为3x3.im2col做的事情就是对于卷积核每一次要处理的小窗,将其展开到新矩阵的一行(列),新矩阵的列(行)数,就是对于一副输入图像,卷积运算的次数(卷积核滑动的次数),如图所示。以最右侧一列为例,卷积核为2x2,所以新矩阵的列数就为4;步长为一,卷积核共滑动4次,行数就为4.再放一张图应该看得更清楚。
-
图示输入为4x4,卷积核为3x3,则新矩阵为9x4 。看到这里我就产生了一个疑问:我们把一个卷积核对应的值展开,到底应该展开为行还是列呢?卷积核的滑动先行后列还是相反?区别在哪?
这其实主要取决于我们使用的框架访存的方式。计算机一次性读取相近的内存是最快的,尤其是当需要把数据送到GPU去计算的时候,这样可以节省访存的时间,以达到加速的目的。不同框架的访存机制不一样,所以会有行列相反这样的区别。在caffe框架下,im2col是将一个小窗的值展开为一行,而在matlab中则展开为列。所以说,行列的问题没有本质区别,目的都是为了在计算时读取连续的内存。
这也解释了我们为什么要通过这个变化来优化卷积。如果按照数学上的步骤做卷积读取内存是不连续的,这样就会增加时间成本。同时我们注意到做卷积对应元素相乘再相加的做法跟向量内积很相似,所以通过im2col将矩阵卷积转化为矩阵乘法来实现。
Im2col, 这里得说明一下: col并不一定是表示列哟,不同平台下实现方式不一样的,如matlab是按列来的,但是caffe却是按照行来存的,其目的都是一样的,都是为了加速内存访问。
每一步的卷积都提前给转换好,放到连续的内存中来,有大量的冗余内存单元被放进来了,这就是典型的空间换时间的例子。

-
a
b
c
d

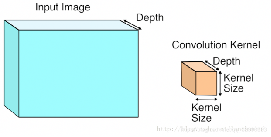
图示 a 常规卷积操作
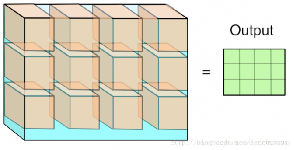
图示 b 3维卷积运算执行完毕,得一个2维的平面
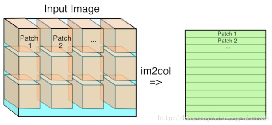
图示 c 将卷积操作的3维立体变为二维矩阵乘法,可以调用BLAS中的GEMM库,按 [kernel_height, kernel_width, kernel_depth] ⇒ 将输入分成 3 维的 patch,并将其展成一维向量
图示 d 此时的卷积操作就可转化为矩阵乘法
2 Winograd
-
The Winograd algorithm was first proposed by Shmuel Winograd in “Arithmetic complexity of computations (1980)” in 1980, and is mainly used to reduce the computational complexity of the FIR filter.
The algorithm is similar to FFT, which maps data to another space, and replaces partial multiplication with addition and subtraction. It achieves obvious acceleration effect under the premise of “addition and subtraction speed is much higher than multiplication operation” (unlike FFT, Winograd maps data to a real space instead of a complex space)
[1] “Fast Algorithms for Convolutional Neural Networks” Lavin and Gray, CVPR 2016.
[2] https://github.com/andravin/wincnn
-
在卷积神经网络当中, 对卷积运算的计算量很敏感, 尤其是在端上设备中, 对于性能的要求更为苛刻。
Winograd算法简介。这个算法用更多的加法来代替乘法,在FPGA上,由于乘法的计算消耗更多的资源和时钟,往往是很慢的。一般的乘法需要借助FPGA中的DSP来计算,DSP的大小有18 bits X 25 bits(Xilinix),的乘法,如果两个浮点数较大,则需要更多的乘法。采用Winograd卷积算法,借助LUT/查找表,来计算乘法,会节省FPGA的资源,加快速度。
winograd算法最早是1980年由Terry Winograd提出的,主要用来减少FIR滤波器的计算量,该算法类似FFT,将数据映射到另一个空间上,用加减运算代替部分乘法运算,在“加减运算速度远高于乘法运算”的前提下达到明显的加速效果(与FFT不同的是,Winograd将数据映射到一个实数空间而非复数空间),当时并没有引起太大的轰动。
在CVPR‘16会议上,拉文等人[1]提出了利用winogrd加速卷积运算,于是winograd加速卷积优化在算法圈里火了一把。网上较多的实现版本为andravin实现的py版本[2]。目前cudnn中计算卷积就使用了该方法。 -
e.g.
input size: 4x4
filter: 3x3
output: 2x2

问题定义
将一维卷积运算定义为F(m,r),m为Output Size,r为Filter Size,则输入信号的长度为m+r−1,卷积运算是对应位置相乘然后求和,输入信号每个位置至少要参与1次乘法,所以乘法数量最少与输入信号长度相同,记为
μ(F(m,r))=m+r−1
在行列上分别进行一维卷积运算,可得到二维卷积,记为F(m×n,r×s),输出为m×n,卷积核为r×s,则输入信号为(m+r−1)(n+s−1),乘法数量至少为
μ(F(m×n,r×s))=μ(F(m,r))μ(F(n,s))=(m+r−1)(n+s−1)
若是直接按滑动窗口方式计算卷积,一维时需要m×r次乘法,二维时需要m×n×r×s次乘法,远大于上面计算的最少乘法次数,这里可以后面看一个例子。
对一个矩阵大小为4 x4的输入,卷积核大小为3 x3,对应的输出为2 x2,正常计算的情况下,滑动窗口或者im2col的计算方法的乘法次数为2x2x3x3 = 36次,而当使用winograd时,对应的乘法次数为u(F(2∗2,3∗3))=(2+3−1)∗(2+3−1)=16,乘法次数明显减少。MULs 减少2.25倍
使用Winograd算法计算卷积快在哪里?一言以蔽之:快在减少了乘法的数量,将乘法数量减少至m+r−1或(m+r−1)(n+s−1)。
怎么减少的?请看下面的例子。
2.1 F(2, 3)
- 如果直接计算 F(2,3):
其中,d0,d1,d2和d1,d2,d3为连续的两个输入序列;
g0,g1,g2为FIR的三个参数;
这个过程一共需要6次乘法,和4次加法
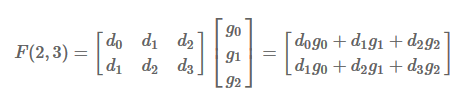
- 而Winograd算法指出,F(2,3) 可以这样计算 a:
其中,b
该用矩阵运算可以表示成:c
其中,⊙表示点乘,而d
g:卷积核
d:输入信号
G:Filter transform矩阵,尺寸(m+r−1)×r
BT:Input transform矩阵,尺寸(m+r−1)×(m+r−1)
AT:Output transform矩阵,尺寸m×(m+r−1)
这……似乎反而把问题变得十分复杂,但实际上它的计算量却真真切切地减少了——
输入信号d上:4次加法(减法)
输出m上:4次乘法,4次加法
在神经网络的推理阶段,卷积核上的元素是固定的,因此g上的运算可以提前算好,预测阶段只需计算一次,可以忽略,所以一共所需的运算次数为d与m上的运算次数之和,即4次乘法和8次加法。
a 由于g是固定的FIR滤波器参数,那么Gg可以提前计算并得到一个 4×1 的列向量
b 由于d是变化的输入序列,所以每次计算FIR的时候都需要对输入d做一个变换BT*d,得到一个 4×1 的列向量,这个过程需要4次加法(注意BT矩阵的元素值)
c 然后Gg和BTd进行点乘,共计4次乘法
d 最后AT与[(Gg)⊙(BTd)]做乘法,共计4次加法
过程a可以提前完成,变换过程b和计算过程c、d共计4次乘法和8次加法,相比于直接FIR的6次乘法、4次加法,乘法次数下降为原来的2/3
(推广到一般情况,直接FIR跟Winograd的乘法次数分别是m×r和m+r−1)。
但天下没有免费的午餐,既然速度得到提升,那么肯定需要付出代价——算法的加速往往是需要以额外的空间为代价的:原先FIR只需要存储3个参数g,但现在需要存储4个参数Gg(推广到一般情况,分别是r和m+r−1)
注意
以上描述的 Winograd 算法只展示了在二维的图像 (更确切的说是 tile) 上的过程, 具体在 ConvNet 的多个 channel 的情况, 直接逐个 channel 按照上述方法计算完然后相加即可;
按照 1. 的思路, 在计算多个 channel 的时候, 仍然有可减少计算次数的地方.
按照 2. 的思路, Winograd 在目前使用越来越多的 depthwise conv 中其优势不明显了.
在 tile 较大的时候, Winograd 方法不适用, 因为, 在做 inverse transform 的时候的计算开销抵消了 Winograd 带来的计算节省.Winograd 会产生误差

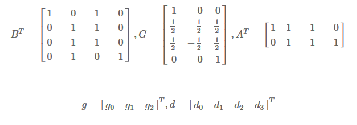
https://hey-yahei.cn/2019/09/18/winograd_theorem/
2.2 F(22, 33)
-
上面只是看了1D的一个例子,2D怎么做呢?论文中一句话带过:
is nested with itself——>与自身嵌套

g is filter of rr, d is image tile of (m+r-1)(m+r-1) -
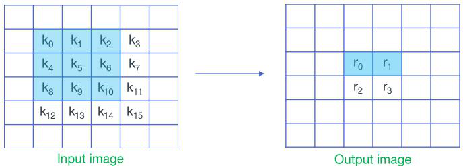
在这一部分中用k来表示输入,w表示权重,r表示输出
对直接卷积来说,该过程一共需要36次乘法和32次加法。
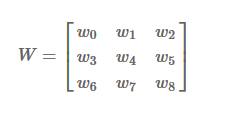
-
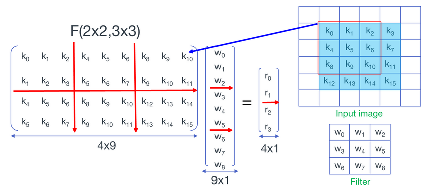
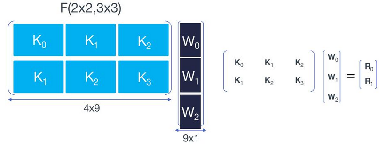
将输入按滑窗分块后展开成向量并堆叠成矩阵,将权重展开成向量——
对矩阵和向量进行分块——
实现方法有 :堆叠实现
-
堆叠实现
其中,Di 是 Ki 对应的输入序列,也即卷积输入的第 i 行
也就是说,F(2×2,3×3)在这里分成了6次F(2,3)以及4次额外的加法,总计24次乘法和44次加法(注意:虽然这里做了6次F(2,3)但是输入序列的变换只需要做4次,所以加法次数是44次而非52次),相比于直接卷积的36次乘法和32次加法,乘法次数跟一维的F(2,3)一样,也下降为原来的2/3,同理也需要付出3倍于F(2,3)额外的空间代价(三个W)


-
嵌套实现
卷积运算为对应位置相乘再相加,上式中,AT[(GW0)⊙(BTD0)]表示长度为4的D0与长度为3的W0卷积结果,结果为长度为2的列向量,其中,(GW0)和(BTD0)均为长度为4的列向量,进一步地,
[(GW0)⊙(BTD0)+(GW1)⊙(BTD1)+(GW2)⊙(BTD2)]可以看成3对长度为4的列向量两两对应位置相乘再相加,结果为长度为4的列向量,也可以看成是4组长度为3的行向量的点积运算,同样,[(GW0)⊙(BTD1)+(GW1)⊙(BTD2)+(GW2)⊙(BTD3)]也是4组长度为3的行向量的内积运算,考虑两者的重叠部分(BTD1)和(BTD2),恰好相当于G[W0 W1 W2]的每一行在BT[d0 d1 d2 d3]的对应行上进行1维卷积,上面我们已经进行了列向量卷积的Winograd推导,行向量的卷积只需将所有左乘的变换矩阵转置后变成右乘就可以了
所谓的nested with itself如图所示,
此时,Winograd算法的乘法次数为16(上图 4×4),而直接卷积的乘法次数为36,降低了2.25倍的乘法计算复杂度。
与F(2,3)同理,可以推导出,F(2×2,3×3)需要16次乘法和56次加法(V=BTdB过程32次加法、M=U⊙V过程16次乘法、Y=ATMA过程24次加法),相比于直接卷积的36次乘法和32次加法,乘法次数下降为原来的16/36。计算量的减少比堆叠实现要明显,但也需要更多的额外空间代价:直接计算只需要存储9个参数的g,F(2×2,3×3)则需要存储16个参数的GgGT(推广到一般情况,分别为r2和(r+m−1)2)
后续讨论中,如非特别说明,二维Winograd均指的是嵌套实现
2.3 G、BT、AT
- F (4,3)

- F (6,3)

- Winograd算法需要推导出相应的变换矩阵G、BT和AT,但具体的推导过程似乎有些复杂,我现在还没弄懂。
所幸 wincnn | github提供了一个解算G、BT、AT的工具,除了前述的F(2,3),常用的还有F(4,3)和F(6,3),它们对应的变换矩阵如下:
注意:与F(2,3)不同,由于F(4,3)和F(6,3)的AT、BT出现了非[0,1,−1]的元素,所以除了点乘过程,还会引入额外的乘法运算。
2.4 3D
- Q :
F(224, 3) ?
3D ?
- Input transform
- Filter transform
- Batched-GEMM
- Output transform
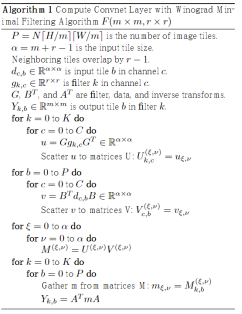
-
上面我们仅仅是针对一个小的image tile,但要将Winograd应用在卷积神经网络中,还需要回答下面两个问题:
是在卷积神经网络中,feature map的尺寸可能很大,难道我们要实现F(224,3)吗?
在卷积神经网络中,feature map是3维的,卷积核也是3维的,3D的winograd该怎么做?
这里直接贴上论文中的算法流程
第一个问题,在实践中,会将input feature map切分成一个个等大小有重叠的tile,在每个tile上面进行winograd卷积。
第二个问题,3维卷积,相当于逐层做2维卷积,然后将每层对应位置的结果相加,下面我们会看到多个卷积核时更巧妙的做法。 -
将转换后的权重分散到矩阵
注意图中的Matrix Multiplication,对应3维卷积中逐channel卷积后的对应位置求和,相当于(m+r−1)2个矩阵乘积,参与乘积的矩阵尺寸分别为⌈H/m⌉⌈W/m⌉×C和C×K,把Channel那一维消掉。

3 Summary
3.1 Performance
- 接下来我们对F(2,3)、F(4,3)、F(6,3)、F(2×2,3×3)、F(4×4,3×3)、F(6×6,3×3)的效果做一简单比较。
从理论的乘法加速比来看(只考虑点乘的乘法),Winograd都有相当理想的加速效果,嵌套实现的F(6×6,3×3)甚至有5.06倍的加速

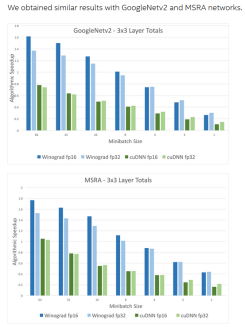
- 以下是一些实际运算中,采用该方法的性能对比结果:
从上面的对比可以看出,利用Winograd算法进行卷积,比NVIDIA的深度学习库cuDNN中的卷积计算快很多。其中cuDNN的卷积是GEMM算法实现。batch_size越大,加速效果越明显,因为越大的batch_size,计算的负载并不是线性的增加,开辟的内存地址和GPU的显存被充分计算应用,增加的一部分空间,平均到一个样本数上,计算时间更短,速度更明显。这个理论在Google的一篇论文上也具体介绍了batch_size的影响。图片来自于Intel官方提供的对比
cudnn中的可用算法已包含了winograd,cudnnConvolutionFwdAlgo_t这个结构体中有已支持的卷积算法,我们默认可以这样设置:
// algorithm cudnnConvolutionFwdAlgo_t algo;
cudnnGetConvolutionForwardAlgorithm(handle,
input_descriptor,
kernel_descriptor,
conv_descriptor,
output_descriptor,
CUDNN_CONVOLUTION_FWD_PREFER_FASTEST,
0,
&algo);


3.2 Ending
-
Winograd算法通过减少乘法次数来实现提速,但是加法的数量会相应增加,同时需要额外的transform计算以及存储transform矩阵,随着卷积核和tile的尺寸增大,就需要考虑加法、transform和存储的代价,而且tile越大,transform矩阵越大,计算精度的损失会进一步增加,所以一般Winograd只适用于较小的卷积核和tile(对大尺寸的卷积核,可使用FFT加速),在目前流行的网络中,小尺寸卷积核是主流,典型实现如F(6×6,3×3)、F(4×4,3×3)、F(2×2,3×3)等,可参见NCNN、FeatherCNN、ARM-ComputeLibrary等源码实现。
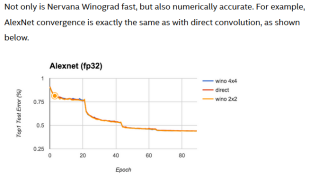
-
Winograd algorithm can speed up by reducing the times of multiplication, but the number of addition will increase correspondingly. At the same time, additional transform calculation and storage of transform matrix are needed. With the size of convolution core and tile increasing, the cost of addition, transform and storage needs to be considered. Moreover, the larger the tile is, the larger the transform matrix is, and the loss of calculation accuracy will further increase
So Winograd is only suitable for small convolution kernel and tile (FFT acceleration can be used for large-scale convolution kernel). In the current popular network, small-scale convolution kernel is the mainstream, and typical implementations such as f (6 × 6,3 × 3), f (4 × 4,3 × 3), f (2 × 2,3 × 3), etc. refer to NCNN, FeatherCNN, ARM-software and other source implementations.
4 Code
from torch import nn
import torch
class WinogradConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, padding=0, stride=1, bias=True):
super(WinogradConv, self).__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.padding = padding
self.stride = stride
self.kernel_size = kernel_size
self.is_bias = bias
self.inner_conv2d = nn.Conv2d(
self.in_channels, self.out_channels, self.kernel_size,
stride=self.stride, padding=self.padding, bias=self.is_bias)
if self.is_bias:
self.bias = self.inner_conv2d.bias
self.weight = self.inner_conv2d.weight
#self.weight.data = self.update_u()
self.NK = torch.FloatTensor(
[[0.75, 0.25, 0.25, -0.25], [0, 1, -1, 0], [-0.25, 0.25, 0.25, 0.75]])
self.NK = self.NK.expand((out_channels, in_channels, 3, 4)).cuda()
self.NKK = torch.FloatTensor(
[[0.75, 0, -0.25], [0.25, 1, 0.25], [0.25, -1, 0.25], [-0.25, 0, 0.75]])
self.NKK = self.NKK.expand((out_channels, in_channels, 4, 3)).cuda()
def update_u(self):
weights = self.inner_conv2d.weight.data
u = torch.zeros((weights.size(0), weights.size(1), 4, 4))
u[:, :, 0, 0] = weights[:, :, 0, 0]
u[:, :, 0, 1] = (weights[:, :, 0, 0] +
weights[:, :, 0, 1]+weights[:, :, 0, 2]) / 2
u[:, :, 0, 2] = (weights[:, :, 0, 0] -
weights[:, :, 0, 1]+weights[:, :, 0, 2]) / 2
u[:, :, 0, 3] = weights[:, :, 0, 2]
u[:, :, 1, 0] = (weights[:, :, 0, 0] +
weights[:, :, 1, 0]+weights[:, :, 2, 0])/2
u[:, :, 1, 1] = (weights[:, :, 0, 0]+weights[:, :, 0, 1]+weights[:, :, 0, 2]
+ weights[:, :, 1, 0] +
weights[:, :, 1, 1]+weights[:, :, 1, 2]
+ weights[:, :, 2, 0]+weights[:, :, 2, 1]+weights[:, :, 2, 2])/4
u[:, :, 1, 2] = (weights[:, :, 0, 0]-weights[:, :, 0, 1]+weights[:, :, 0, 2]
+ weights[:, :, 1, 0] -
weights[:, :, 1, 1]+weights[:, :, 1, 2]
+ weights[:, :, 2, 0]-weights[:, :, 2, 1]+weights[:, :, 2, 2])/4
u[:, :, 1, 3] = (weights[:, :, 0, 2] +
weights[:, :, 1, 2]+weights[:, :, 2, 2])/2
u[:, :, 2, 0] = (weights[:, :, 0, 0] -
weights[:, :, 1, 0]+weights[:, :, 2, 0])/2
u[:, :, 2, 1] = (weights[:, :, 0, 0]+weights[:, :, 0, 1]+weights[:, :, 0, 2]
- weights[:, :, 1, 0] -
weights[:, :, 1, 1]-weights[:, :, 1, 2]
+ weights[:, :, 2, 0]+weights[:, :, 2, 1]+weights[:, :, 2, 2])/4
u[:, :, 2, 2] = (weights[:, :, 0, 0]-weights[:, :, 0, 1]+weights[:, :, 0, 2]
- weights[:, :, 1, 0] +
weights[:, :, 1, 1]-weights[:, :, 1, 2]
+ weights[:, :, 2, 0]-weights[:, :, 2, 1]+weights[:, :, 2, 2])/4
u[:, :, 2, 3] = (weights[:, :, 0, 2] -
weights[:, :, 1, 2]+weights[:, :, 2, 2])/2
u[:, :, 3, 0] = weights[:, :, 2, 0]
u[:, :, 3, 1] = (weights[:, :, 2, 0] +
weights[:, :, 2, 1]+weights[:, :, 2, 2]) / 2
u[:, :, 3, 2] = (weights[:, :, 2, 0] -
weights[:, :, 2, 1]+weights[:, :, 2, 2]) / 2
u[:, :, 3, 3] = weights[:, :, 2, 2]
return u
def update_k(self):
if self.weight.shape[2] == 4:
weights = self.NK.matmul(self.weight.data.cuda()).matmul(self.NKK)
self.inner_conv2d.weight.data = weights.cuda()
self.weight.data = weights
# self.inner_conv2d.weight = weights.cuda()
else:
self.inner_conv2d.weight.data = self.weight.cuda()
# self.inner_conv2d.weight = self.inner_conv2d.weight.cuda()
return
def forward(self, input_feature):
self.update_k()
out = self.inner_conv2d(input_feature)
return out
if __name__ == "__main__":
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = WinogradConv(3, 2, 3)
self.conv2 = WinogradConv(2, 1, 3)
self.fc1 = nn.Linear(12*12, 2)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = x.view(-1, 12*12)
x = self.fc1(x)
return x
def test():
loss_fun = nn.CrossEntropyLoss()
input_feature = torch.randn((4, 3, 16, 16)).cuda()
label = torch.LongTensor([0, 1, 0, 1]).cuda()
winograd_conv = WinogradConv(3, 5, 3, bias=False)
model = Net()
model.cuda()
all_parameters = list(model.parameters())
for i in model.modules():
if type(i) == WinogradConv:
all_parameters.extend(list(i.inner_conv2d.parameters()))
optimizer = torch.optim.SGD(all_parameters, lr=1)
for i in range(5):
optimizer.zero_grad()
output = model(input_feature)
loss = loss_fun(output, label)
loss.backward()
optimizer.step()
for i in model.modules():
if type(i) == WinogradConv:
i.weight.data = i.update_u()
test()