传送门
- 文献原文可前往其收录处《混沌映射与比特重组的图像加密》.
- 文献的算法流程 (包括算法勘误, 算法整理) 可以参见博文《《混沌映射与比特重组的图像加密》(平萍等)一文的算法流程》.
- 对算法背后一些理论的分析可以参见博文《《混沌映射与比特重组的图像加密》(平萍等)一文的算法分析》.
- 对算法及其改进形式的仿真实验可以参见博文《《混沌映射与比特重组的图像加密》(平萍等)一文的仿真实验 (基于Matlab)》.
- 对算法的性能分析可以参见博文《《混沌映射与比特重组的图像加密》(平萍等)一文的性能分析(一)-- 敏感性分析 (基于Matlab)》 以及 《《混沌映射与比特重组的图像加密》(平萍等)一文的性能分析(二)-- 相关性, 安全性强度, 计算用时分析 (基于Matlab)》.
- 原文算法的实现可以参见博文《《混沌映射与比特重组的图像加密》(平萍等)一文的算法实现(基于Matlab)》.
算法改进
博文《《混沌映射与比特重组的图像加密》(平萍等)一文的算法流程》中的 对原文加密算法的主要勘误 一节的第1点指出了基于原文所给的资料, 只能确定原文的加密 (和解密) 算法适用于尺寸为 N × N N \times N N×N的方形图像 (具体原因可参见原博文). 这个限制的形成来源于可逆Henon映射表达式
{ x ( n + 1 ) = 1 − a x 2 ( n ) + y ( n ) m o d N , y ( n + 1 ) = x ( n ) + c m o d N . \left\{ \begin{aligned} & x\left( n+1 \right)=1-a{
{x}^{2}}\left( n \right)+y\left( n \right)\text{ }\bmod N, \\ & y\left( n+1 \right)=x\left( n \right)+c\text{ }\bmod N. \\ \end{aligned} \right. {
x(n+1)=1−ax2(n)+y(n) modN,y(n+1)=x(n)+c modN.
中第一, 二式的模数都要求是 N N N. 而原文加密算法涉及可逆Henon映射的步骤只有《《混沌映射与比特重组的图像加密》(平萍等)一文的算法流程》中的 整理后的加密算法步骤 中的 第(9)步: 应用可逆Henon映射对8个 N × N N \times N N×N比特矩阵进行置乱. 事实上, 当明文图像尺寸为 M × N M \times N M×N时, 该步骤中的8个比特矩阵的尺寸也分别为 M × N M \times N M×N. 我们指出, 通过添加一些处理, 也可以在 M × N M \times N M×N的矩阵上应用同上的可逆Henon映射来置乱.
任取1个 M × N M \times N M×N的比特矩阵 B i ( i = 1 , 2 , ⋯ , 8 ) { {B}_{i}}\left( i=1,2,\cdots ,8 \right) Bi(i=1,2,⋯,8)为例来说明操作方法. 当 M = N M = N M=N时就是矩阵为方阵的情况, 此时不用再添加其他处理. 当 M ≠ N M\ne N M=N时, 不妨令 N > M N \gt M N>M, 我们欲使用滑动窗口法. 初始构建一个大小为 δ × δ = M × M \delta \times \delta = M \times M δ×δ=M×M的滑动窗口, 设置其滑动步长为 δ = M \delta = M δ=M, 令窗口初始位置在矩阵 B i B_i Bi的最左端, 规定窗口滑动方向为向右. 以下步骤的执行基于带余除法的思想.
算法步骤
Step 1
对窗口内的矩阵进行 n i n_i ni次Henon映射置乱, n i n_i ni是对应于该比特矩阵 B i B_i Bi的置乱次数.
Step 2
①若窗口的滑动方向为向右, 判断窗口右侧矩阵的列数是否 ≥ δ \ge \delta ≥δ. 若是, 将窗口向右滑动 δ \delta δ格, 然后转到Step 1; 否则转到Step 3.
②若窗口的滑动方向为向下, 判断窗口下侧矩阵的行数是否 ≥ δ \ge \delta ≥δ. 若是, 将窗口向下滑动 δ \delta δ格, 然后转到Step 1; 否则转到Step 3.
Step 3
①若窗口的滑动方向为向右, 当窗口右侧刚好没有矩阵区域, 即右侧矩阵列数 = 0 =0 =0时, 则该比特矩阵 B i B_i Bi的置乱完全结束, 退出算法; 当窗口右侧有 a × b a \times b a×b的矩阵区域 ( b > 0 ) \left( b>0 \right) (b>0)时, 置窗口的大小为 δ × δ = b × b \delta \times \delta = b \times b δ×δ=b×b, 置窗口的滑动步长为 δ = b \delta = b δ=b, 将窗口移动到剩余矩阵区域的最上方, 并规定窗口滑动方向为向下. 转到Step 1.
②若窗口的滑动方向为向下, 当窗口下方刚好没有矩阵区域, 即下方矩阵行数 = 0 =0 =0时, 则该比特矩阵 B i B_i Bi的置乱完全结束, 退出算法; 当窗口下方有 a × b a \times b a×b的矩阵区域 ( a > 0 ) \left( a>0 \right) (a>0)时, 置窗口的大小为 δ × δ = a × a \delta \times \delta = a \times a δ×δ=a×a, 置窗口的滑动步长为 δ = a \delta = a δ=a, 将窗口移动到剩余矩阵区域的最左端, 并规定窗口滑动方向为向右. 转到Step 1.
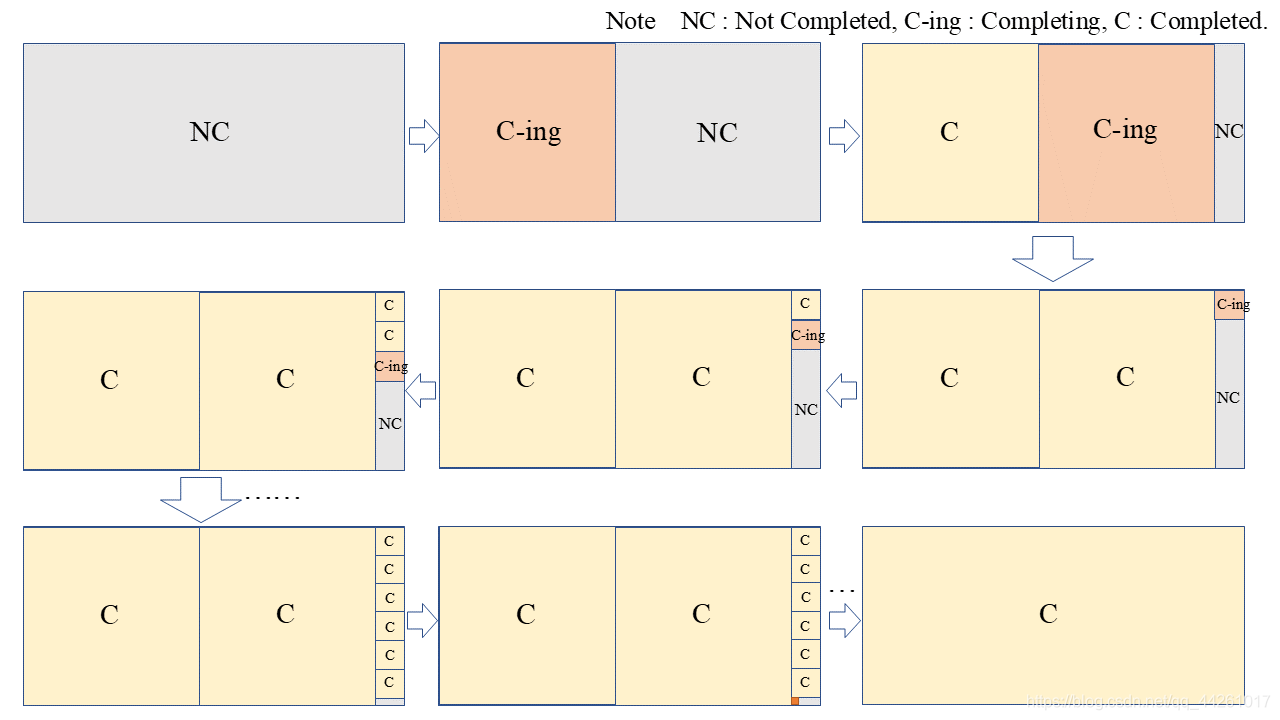
注意, 对任意有限大小的矩阵, 由辗转相除法的思想和性质, 上述算法执行步骤总是有限的.
算法展望 (初步)
以下涉及的"步骤x"均来源于博文《《混沌映射与比特重组的图像加密》(平萍等)一文的算法流程》中的 整理后的加密算法步骤 一节.
(1) 将明文图像 I I I的大小拓展到任意尺寸 M × N M\times N M×N的情况, 步骤(1)中的式(1’)应改为
s = ∑ j = 1 N ∑ i = 1 M I ( i , j ) . s=\sum\limits_{j=1}^{N}{\sum\limits_{i=1}^{M}{I\left( i,j \right)}}. s=j=1∑Ni=1∑MI(i,j).
式(2’)应改为
μ = 2 s / M × N × 255 . \mu ={
{2}^{
{s}/{M\times N\times 255}\;}}. μ=2s/M×N×255.
步骤(3)中的序列 E E E的长度应该为 M M M, E = { e 1 , e 2 , ⋯ , e M } E=\left\{ {
{e}_{1}},{
{e}_{2}},\cdots ,{
{e}_{M}} \right\} E={
e1,e2,⋯,eM}.
步骤(5)中的序列 R R R的长度应该为 M × N M\times N M×N, R = { r 1 , r 2 , ⋯ , r M × N } R=\left\{ {
{r}_{1}},{
{r}_{2}},\cdots ,{
{r}_{M\times N}} \right\} R={
r1,r2,⋯,rM×N}.
步骤(7)中的位置响铃 P E {
{P}^{E}} PE的长度应该为 M M M, P E = { p 1 E , p 2 E , ⋯ , p M E } {
{P}^{E}}=\left\{ {
{p}_{1}}^{E},{
{p}_{2}}^{E},\cdots ,{
{p}_{M}}^{E} \right\} PE={
p1E,p2E,⋯,pME}.
原步骤中其他涉及类似 N × N N \times N N×N的表述需要的话也改为 M × N M \times N M×N. 以下展望均建立在原加密算法已经拓展到适用于任意大小明文图像的情况.
(2) 步骤(6)中将像素矩阵中每个像素转换成8位二进制数.
① 这8个数字默认是按横向排列的, 因此得到的矩阵是 M × ( 8 × N ) M\times \left( 8\times N \right) M×(8×N)的大小. 作为拓展, 也可将这8个数字按照纵向排列, 得到一个 ( 8 × M ) × N \left( 8\times M \right)\times N (8×M)×N的矩阵.
② 原文默认这8个数字是紧密排列的, 作为拓展, 也可以将这8个数字两两之间隔开 N N N个(横向排列的情况下)或者 M M M个(纵向排列的情况下)排列, 或者设计其他更加复杂的排列方式.
③ 此外, 该步骤中得到大小为 M × ( 8 × N ) M\times \left( 8\times N \right) M×(8×N)或者 ( 8 × M ) × N \left( 8\times M \right)\times N (8×M)×N的矩阵后, 可以考虑再将里面的 8 8 8个 M × N M\times N M×N的比特矩阵旋转合适的角度(不过要保证旋转后的8个小矩阵能够拼接在一起), 如大矩阵为 M × ( 8 × N ) M\times \left( 8\times N \right) M×(8×N)尺寸, 从左到右每个大小为 M × N M\times N M×N的小矩阵可以逆时针旋转90度或者顺时针旋转90度, 每个矩阵旋转的方向可以不一样. 又或者当 M = N M=N M=N时, 8个 M × N = N × N M\times N=N\times N M×N=N×N的小矩阵各自可以自由地选择逆时针旋转90度, 180度或者270度.
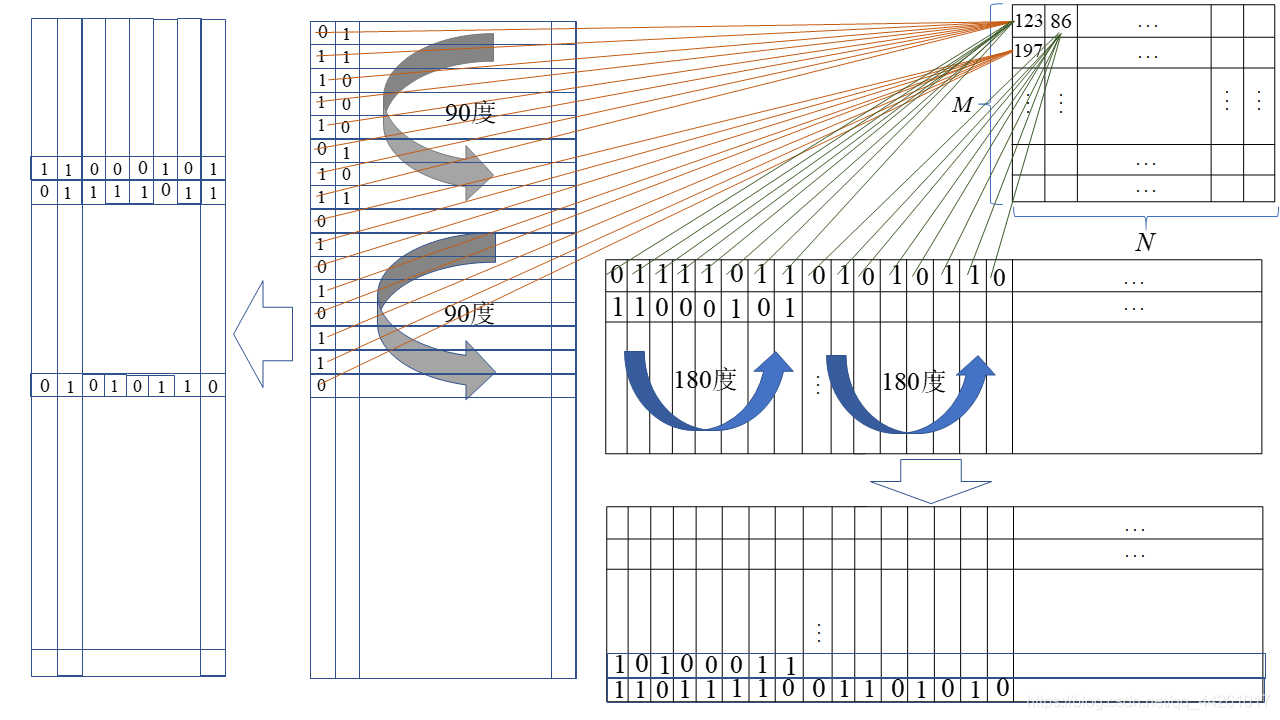
(3) 步骤(7)中默认将序列 E E E按升序排序得到位置向量 P E {
{P}^{E}} PE, 作为拓展, 也可以将 E E E按降序排序得到位置向量 P E {
{P}^{E}} PE, 或者将 E E E中的奇数索引的数据单独按升序(降序)排列得到 P 1 E P_{1}^{E} P1E, 偶数索引的数据单独按升序(降序)排列得到 P 2 E P_{2}^{E} P2E, 再令 P E = [ P 1 E , P 2 E ] {
{P}^{E}}=\left[ P_{1}^{E},P_{2}^{E} \right] PE=[P1E,P2E]或者 P E = [ P 2 E , P 1 E ] {
{P}^{E}}=\left[ P_{2}^{E},P_{1}^{E} \right] PE=[P2E,P1E]得到位置向量 P E {
{P}^{E}} PE, 或者可以设计更加复杂的排序方式来得到不同的位置向量 P E {
{P}^{E}} PE.
步骤(8)中位置向量 P F {
{P}^{F}} PF的产生也可同理进行拓展.
(4) 步骤(9)中对第 i i i个比特矩阵默认按下式计算控制参数 a i , c i {
{a}_{i}},\text{ }{
{c}_{i}} ai, ci和迭代次数 n i {
{n}_{i}} ni
a i = [ f N ⋅ ( i − 1 ) + 1 × 10 14 ] m o d 2 8 , (1) {
{a}_{i}}=\left[ {
{f}_{N\centerdot \left( i-1 \right)+1}}\times {
{10}^{14}} \right]\text{ }\bmod {
{2}^{8}}, \tag{1} ai=[fN⋅(i−1)+1×1014] mod28,(1)
c i = [ f N ⋅ ( i − 1 ) + 1 2 × 10 14 ] m o d 2 8 , (2) {
{c}_{i}}=\left[ {
{f}_{N\centerdot \left( i-1 \right)+1}}^{2}\times {
{10}^{14}} \right]\text{ }\bmod {
{2}^{8}}, \tag{2} ci=[fN⋅(i−1)+12×1014] mod28,(2)
n i = 1 + ( [ f N ⋅ ( i − 1 ) + 1 × 10 14 ] m o d 5 ) . (3) {
{n}_{i}}=1+\left( \left[ {
{f}_{N\centerdot \left( i-1 \right)+1}}\times {
{10}^{14}} \right]\text{ }\bmod 5 \right).\text{ } \tag{3} ni=1+([fN⋅(i−1)+1×1014] mod5). (3)
三个式子均使用了混沌序列 F F F里面的第 N ⋅ ( i − 1 ) + 1 N\centerdot \left( i-1 \right)+1 N⋅(i−1)+1个值 f N ⋅ ( i − 1 ) + 1 {
{f}_{N\centerdot \left( i-1 \right)+1}} fN⋅(i−1)+1. 作为拓展, 可以让式(1), (2), (3)使用混沌序列 F F F中的其他的值, 比如将式(1), (2), (3)改写成
a i = [ f N ⋅ ( i − 1 ) + 1 × 10 14 ] m o d 2 8 , (1’) {
{a}_{i}}=\left[ {
{f}_{N\centerdot \left( i-1 \right)+1}}\times {
{10}^{14}} \right]\text{ }\bmod {
{2}^{8}}, \tag{1'} ai=[fN⋅(i−1)+1×1014] mod28,(1’)
c i = [ f N ⋅ ( i − 1 ) + [ N 2 ] 2 × 10 14 ] m o d 2 8 , (2’) {
{c}_{i}}=\left[ {
{f}_{N\centerdot \left( i-1 \right)+\left[ \frac{N}{2} \right]}}^{2}\times {
{10}^{14}} \right]\text{ }\bmod {
{2}^{8}}, \tag{2'} ci=[fN⋅(i−1)+[2N]2×1014] mod28,(2’)
n i = 1 + ( [ f N ⋅ i − 1 × 10 14 ] m o d 5 ) . (3’) {
{n}_{i}}=1+\left( \left[ {
{f}_{N\centerdot i-1}}\times {
{10}^{14}} \right]\text{ }\bmod 5 \right).\tag{3'} ni=1+([fN⋅i−1×1014] mod5).(3’)
此外, 若希望对第 i i i个比特平面迭代Henon映射的最大次数不是5次, 例如改成10次, 20次, 则可以将式(3)中的 m o d 5 \bmod 5 mod5改写成 m o d 10 , m o d 20 \bmod 10,\text{ }\bmod 20 mod10, mod20.
(5) 步骤(1)中计算Tent混沌系统初始迭代次数 k k k的公式是
k = 10 3 + ( s m o d 10 3 ) . k={
{10}^{3}}+\left( s\text{ }\bmod {
{10}^{3}} \right). k=103+(s mod103).
若希望初始迭代的最小次数不是 10 3 {
{10}^{3}} 103, 例如改成 500 , 10 4 500,\text{ }{
{10}^{4}} 500, 104次, 则可以将上式改写成
k = 500 + ( s m o d 500 ) 或 k = 10 4 + ( s m o d 10 4 ) . k=500+\left( s\text{ }\bmod 500 \right)\text{ }或\text{ }k={
{10}^{4}}+\left( s\text{ }\bmod {
{10}^{4}} \right). k=500+(s mod500) 或 k=104+(s mod104).
初始迭代的最小次数其实也是可以作为另外的一个密钥输入到加密算法中。
(6) 步骤(10)中默认将各自完成相应次数Henon映射迭代的8个比特矩阵按垂直于比特矩阵平面的方向合并, 作为拓展, 也可以在8个比特矩阵垂直排列的同时, 将其中部分或全部矩阵旋转合适的角度后再合并, 比如由上至下将第1, 3, 5, 7个矩阵逆时针旋转90度, 将第2, 4, 6, 8个矩阵顺时针旋转90度, 然后再合并. 或者当大比特矩阵的大小是 M × ( 8 × N ) M\times \left( 8\times N \right) M×(8×N)时, 直接将每8个横向相邻像素的灰度值合并, 转化为十进制像素值(当大比特矩阵的大小是 ( 8 × M ) × N \left( 8\times M \right)\times N (8×M)×N时, 则将每8个纵向相邻像素的灰度值合并, 转化为十进制像素值). 或者设计其他更加复杂的合并方式.

(7) 本文上面介绍的 算法改进 部分, 关于滑动窗口的属性有滑动窗口大小, 滑动窗口移动步长, 滑动窗口每一阶段的初始位置 (这里一个阶段的末尾的标志是窗口再按照规定方向滑动会超出区域范围) , 滑动窗口的滑动方向. 以刚开始的滑动窗口为例:
① 本文上面设置刚开始的滑动窗口大小为 min { M , N } × min { M , N } \min \left\{ M,N \right\} \times \min \left\{ M,N \right\} min{ M,N}×min{ M,N}, 实际上在严格限制滑动窗口为方形窗口的前提下, 可以调整滑动窗口的大小为 δ × δ \delta \times \delta δ×δ, 其中 δ ∈ Z > 0 , 2 ≤ δ ≤ min { M , N } \delta \in { {\mathbb{Z}}_{>0}},\text{ }2\le \delta \le \min \left\{ M,N \right\} δ∈Z>0, 2≤δ≤min{ M,N}. 需要注意的是窗口大小变小后, 原来的移动策略也需要作出相应更加复杂的调整. 而滑动窗口越小, 一般相应地需要的计算量也会变多.
② 对于滑动窗口移动步长, 作为拓展, 其实不一定要等于滑动窗口的尺寸. 例如滑动窗口的大小为 δ × δ \delta \times \delta δ×δ, 则可以设置移动步长为 [ δ 2 ] \left[ \frac{\delta }{2} \right] [2δ], 此时移动前窗口 I 1 I_1 I1和移动后的窗口 I 2 I_2 I2的交非空, 但这并不会给算法带来破坏, 只不过交集区域的像素会进行多起码一倍计算量的Henon映射置乱而已, 某种意义上讲, 可以使得算法结构更具复杂性, 更稳定.


③ 对于滑动窗口每一阶段的初始位置, 可以是最左端, 最右端, 最上方, 最下方, 或者是其他非平凡的位置, 只不过初始位置一改, 相应的窗口移动策略也需要作出相应调整.
④ 对于滑动窗口滑动方向, 一般就是向左滑动, 向右滑动, 向上滑动, 向下滑动. 或者可以设计其他更加复杂的滑动方式, 只不过需要设计相应的滑动策略, 以及验证这样的滑动方式和滑动策略能不能让起码绝大部分的像素发生了Henon映射置乱, 确保这样的操作是有效的.