第十讲（第一版第十一讲）-位姿图优化部分

误差关于位姿的雅克比矩阵推导

今天看到后端优化的关于位姿图优化部分，对于误差关于两个位姿的雅克比矩阵推导部分理解遇到了一些困难。书中直接给$T_i$和$T_j$各乘了一个左扰动，然后就开始推导了。
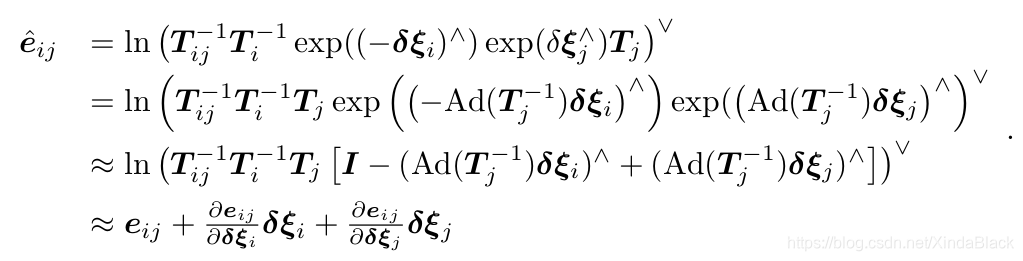倒数第三行到倒数第二行的近似运用了Taylor Expansion，倒数第二行到倒数第一行的近似是什么原理就不太清楚了。（希望如果有知道其中原理的大神看到了，能在评论里给出解释或者推导过程的连接，谢谢！）

现在我给出我自己的理解，分别求对两个位姿的雅克比矩阵。令$T_{ij}^{-1}{T}_i^{-1}{T}_j$的李代数为${\xi }_e$，给李群$T_i$一个左扰动，那么误差可以表示为
$$\widehat{{\xi }_e}=\ln \left(T_{ij}^{-1}{T}_i^{-1}\exp \right((-\delta {\xi }_i{)}^{\wedge })T_j{)}^{\vee }$$
注意，书中误差用$e_{ij}$表示，按照定义的形式应该是一个$6\times 1$维的向量，是个李代数，所以用${\xi }_e$表示感觉不会存在误导。利用SE(3)上的伴随性质
$$\widehat{{\xi }_e}=\ln \left(T_{ij}^{-1}{T}_i^{-1}{T}_j\exp \right((-\mathrm{A}\mathrm{d}(T_j^{-1})\delta {\xi }_i{)}^{\wedge }){)}^{\vee }$$
利用BCH右乘近似
$$\widehat{{\xi }_e}=\ln \left(\exp \right({\xi }_e^{\wedge }\left)\exp \right((-\mathrm{A}\mathrm{d}(T_j^{-1})\delta {\xi }_i{)}^{\wedge }){)}^{\vee }=-J_r^{-1}\mathrm{A}\mathrm{d}(T_j^{-1})\delta {\xi }_i+{\xi }_e$$
再根据李代数的求导
$$\frac{\partial e_{ij}}{\partial \delta {\xi }_i}=\underset{\delta {\xi }_i\to 0}{\lim }\frac{-J_r^{-1}\mathrm{A}\mathrm{d}(T_j^{-1})\delta {\xi }_i+{\xi }_e-{\xi }_e}{\delta {\xi }_i}=-J_r^{-1}\mathrm{A}\mathrm{d}(T_j^{-1})$$
同理，给李群$T_j$一个左扰动，在根据李代数求导，可以求得
$$\frac{\partial e_{ij}}{\partial \delta {\xi }_i}=J_r^{-1}\mathrm{A}\mathrm{d}(T_j^{-1})$$

课后习题1

根据上面的思路，如果误差定义为$\Delta {\xi }_{ij}={\xi }_i\circ {\xi }_j^{-1}$，左扰动雅克比矩阵可以表示为
$$\frac{\partial e_{ij}}{\partial \delta {\xi }_i}=J_r^{-1}\mathrm{A}\mathrm{d}(T_j)\mathrm{A}\mathrm{d}(T_i^{-1})$$
$$\frac{\partial e_{ij}}{\partial \delta {\xi }_i}=-J_r^{-1}$$
按照此结果改写pose_graph_g2o_lie.cpp中误差和雅克比矩阵

//error
_error = (_measurement.inverse() * v1 * v2.inverse()  ).log();
//jacobian
_jacobianOplusXi = J * v2.Adj() * v1.inverse().Adj();
_jacobianOplusXj = -J;

结果没有符合预期，误差是下降了，但是优化结束了还是很大，g2o_viewer显示的结果也不对。不过将linearizeOplus()函数注释掉，采用数值方式求解的雅克比矩阵，最后结果还是一样。个人猜测可能是这样误差定义成这样可能和g2o内部代码设定不匹配，当然也可能是上面的雅克比矩阵没求对，所以希望有这样尝试过的也可以分享下经验。 分析之后，应该是sphere.g2o中保存边的观测值（即位姿间的相对运动）应该是按照$T_i^{-1}{T}_j$定义的，而不是按照$T_i{T}_j^{-1}$定义，这样用此种方式定义的误差进行优化将得不到预期的结果。
还有一个问题就是左乘扰动和右乘扰动推导的雅克比矩阵不一样，用右乘扰动推导的雅克比矩阵优化，得不到预期的结果。这应该是位姿矩阵左乘和右乘不同导致的，一般SLAM里求的位姿指的都是相对于世界坐标系的绝对位姿，即左乘；而右乘是相对于动坐标系的位姿，可以理解为对前一帧图像的相对位姿。sphere.g2o中保存的顶点应该是相对于世界坐标系下的位姿。因此，如果图优化的顶点的是关键帧之间的相对位姿，则应该用右扰动模型求解的结果；如果顶点保存的是相对于固定坐标的位姿，则应该使用左扰动模型求解的结果。（没有在实际代码中验证过）

optimizing ...
iteration= 0     chi2= 15212918696.119320        time= 0.928117  cumTime= 0.928117       edges= 9799     schur= 0        lambda= 81.350858   levenbergIter= 1
iteration= 1     chi2= 11386678732.912115        time= 0.978504  cumTime= 1.90662        edges= 9799     schur= 0        lambda= 54.233905   levenbergIter= 1
iteration= 2     chi2= 5105775457.680527         time= 1.01027   cumTime= 2.91689        edges= 9799     schur= 0        lambda= 36.155937   levenbergIter= 1
iteration= 3     chi2= 3636537945.099213         time= 1.00972   cumTime= 3.92661        edges= 9799     schur= 0        lambda= 24.103958   levenbergIter= 1
iteration= 4     chi2= 675549387.141574  time= 0.992889  cumTime= 4.9195         edges= 9799     schur= 0 lambda= 16.069305  levenbergIter= 1
iteration= 5     chi2= 249002379.412620  time= 0.971525  cumTime= 5.89102        edges= 9799     schur= 0 lambda= 10.712870  levenbergIter= 1
iteration= 6     chi2= 147527240.236920  time= 1.00219   cumTime= 6.89322        edges= 9799     schur= 0 lambda= 7.141913   levenbergIter= 1
iteration= 7     chi2= 79441445.003757   time= 0.966643  cumTime= 7.85986        edges= 9799     schur= 0 lambda= 4.445619   levenbergIter= 1
iteration= 8     chi2= 65455378.789084   time= 1.00436   cumTime= 8.86422        edges= 9799     schur= 0 lambda= 1.906949   levenbergIter= 1
iteration= 9     chi2= 61760426.506496   time= 0.940925  cumTime= 9.80515        edges= 9799     schur= 0 lambda= 0.635650   levenbergIter= 1
iteration= 10    chi2= 59864696.972565   time= 1.00284   cumTime= 10.808         edges= 9799     schur= 0 lambda= 0.211883   levenbergIter= 1
iteration= 11    chi2= 59741695.565524   time= 1.00289   cumTime= 11.8109        edges= 9799     schur= 0 lambda= 0.141255   levenbergIter= 1
iteration= 12    chi2= 59624909.837083   time= 0.955693  cumTime= 12.7666        edges= 9799     schur= 0 lambda= 0.094170   levenbergIter= 1
iteration= 13    chi2= 57542133.582117   time= 1.9179    cumTime= 14.6845        edges= 9799     schur= 0 lambda= 0.125560   levenbergIter= 2
iteration= 14    chi2= 56043735.219484   time= 1.92567   cumTime= 16.6101        edges= 9799     schur= 0 lambda= 0.167052   levenbergIter= 2
iteration= 15    chi2= 55731974.147674   time= 1.00317   cumTime= 17.6133        edges= 9799     schur= 0 lambda= 0.111368   levenbergIter= 1
iteration= 16    chi2= 54104140.413337   time= 1.92121   cumTime= 19.5345        edges= 9799     schur= 0 lambda= 0.141591   levenbergIter= 2
iteration= 17    chi2= 53804036.461193   time= 1.00997   cumTime= 20.5445        edges= 9799     schur= 0 lambda= 0.094394   levenbergIter= 1
iteration= 18    chi2= 52174388.910775   time= 1.82121   cumTime= 22.3657        edges= 9799     schur= 0 lambda= 0.125859   levenbergIter= 2
iteration= 19    chi2= 51901913.851112   time= 1.01241   cumTime= 23.3781        edges= 9799     schur= 0 lambda= 0.083906   levenbergIter= 1
iteration= 20    chi2= 50389317.789719   time= 1.90794   cumTime= 25.286         edges= 9799     schur= 0 lambda= 0.111875   levenbergIter= 2
iteration= 21    chi2= 50188802.496751   time= 1.0043    cumTime= 26.2903        edges= 9799     schur= 0 lambda= 0.074583   levenbergIter= 1
iteration= 22    chi2= 49380588.813712   time= 0.940104  cumTime= 27.2304        edges= 9799     schur= 0 lambda= 0.049722   levenbergIter= 1
iteration= 23    chi2= 48552200.604526   time= 0.99819   cumTime= 28.2286        edges= 9799     schur= 0 lambda= 0.033148   levenbergIter= 1
iteration= 24    chi2= 48405897.723593   time= 1.00536   cumTime= 29.234         edges= 9799     schur= 0 lambda= 0.022099   levenbergIter= 1
iteration= 25    chi2= 48285647.351651   time= 1.01389   cumTime= 30.2479        edges= 9799     schur= 0 lambda= 0.014732   levenbergIter= 1
iteration= 26    chi2= 48144893.438943   time= 1.00391   cumTime= 31.2518        edges= 9799     schur= 0 lambda= 0.009822   levenbergIter= 1
iteration= 27    chi2= 48008186.430056   time= 0.851683  cumTime= 32.1035        edges= 9799     schur= 0 lambda= 0.006548   levenbergIter= 1
iteration= 28    chi2= 47901148.863662   time= 1.00447   cumTime= 33.1079        edges= 9799     schur= 0 lambda= 0.004365   levenbergIter= 1
iteration= 29    chi2= 47839926.122896   time= 1.00723   cumTime= 34.1152        edges= 9799     schur= 0 lambda= 0.001455   levenbergIter= 1
saving optimization results ...