本次分享动态规划模型中的数字三角形模型
动态规划做法和新就是找到状态标识和状态转移方程
状态的寻找一般从题目中获得,每一个状态对应数组的一个维度
分析状态转移方程一般从最后一步去看,这样比较好推出方程
所谓最后一步就是指第n-1中状态到第n中状态的转移过程,推出后进而推出所有
先看引例
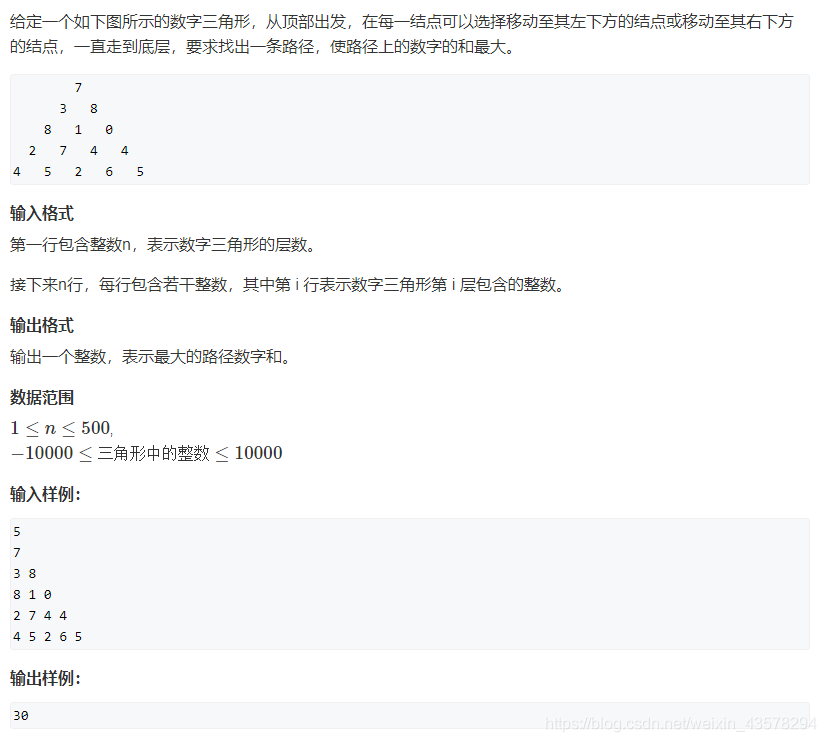
题目分析:
状态表示:
从题目中获得,最上层节点走到最下层节点的最大路径,每一种走法所经过的每个点对应两个状态,x,y坐标,分析出这两个状态来源于如何将数字三角形存储下来,很明显二维矩阵,分别对应x,y坐标---->f[i][j]表示走到第i行第j列的路径和最大值。
状态转移:
题目中要求路径走法为:经过第i行第j列的元素的路径必须经过第i-1行j列或第i-1行j-1列.
所以不难分析出状态转移方程f[i][j]=max(f[i-1][j],f[i-1][j-1])+w[i][j];
代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 510;
int g[N][N];
int f[N][N];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>g[i][j];
}
}
memset(f,-0x3f,sizeof f);
f[1][1]=g[1][1];
for(int i=2;i<=n;i++){
for(int j=1;j<=n;j++){
f[i][j]=max(f[i-1][j],f[i-1][j-1])+g[i][j];
}
}
int res=-0x3f3f3f3f;
for(int i=1;i<=n;i++){
res=max(res,f[n][i]);
}
cout<<res<<endl;
return 0;
}
数字三角形模型是一类动态规划问题的模型,我们下来可以看一下其他类型的题目:
例1:来源:信息学奥赛一本通

题目分析:
状态表示:
和数字三角形模型相同,f[i][j]表示经过第i行第j列所采摘的花生最大数量。
状态计算:
本题目需注意走法~~~
f[i][j]=max(f[i][j],f[i-1][j]+w[i][j]);
f[i][j]=max(f[i][j],f[i][j-1]+w[i][j]);
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n,m,t;
int g[N][N];
int f[N][N];
int main(){
cin>>t;
while(t--){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>g[i][j];
}
}
memset(f,0,sizeof f);
// f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j]=max(f[i][j],f[i-1][j]+g[i][j]);
f[i][j]=max(f[i][j],f[i][j-1]+g[i][j]);
}
}
cout<<f[n][m]<<endl;
}
return 0;
}
例2:来源:信息学奥赛一本通

题目分析:
状态表示:
与上述两题类似 f[i][j]表示经过第i行第j列所需的最少费用
状态计算:
f[i][j]=min(f[i][j],f[i-1][j]+g[i][j]);
f[i][j]=min(f[i][j],f[i][j-1]+g[i][j]);
f[i][j]=min(f[i][j],f[i+1][j]+g[i][j]);
f[i][j]=min(f[i][j],f[i][j+1]+g[i][j]);
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 110;
int f[N][N];
int g[N][N];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>g[i][j];
}
}
memset(f,0x3f,sizeof f);
f[1][1]=g[1][1];
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
f[i][j]=min(f[i][j],f[i-1][j]+g[i][j]);
f[i][j]=min(f[i][j],f[i][j-1]+g[i][j]);
f[i][j]=min(f[i][j],f[i+1][j]+g[i][j]);
f[i][j]=min(f[i][j],f[i][j+1]+g[i][j]);
}
}
cout<<f[n][n]<<endl;
return 0;
}
例3:来源:NOIP提高组2000,洛谷

本体分析借助图片辅助理解:
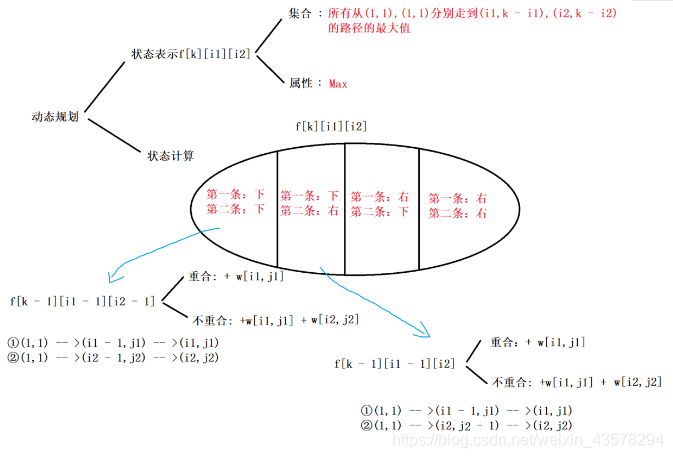
1、f[i1,j1,i2,j2]表示所有从(1,1),(1,1)分别走到(i1,j1),(i2,j2)的路径的最大值
2、由于走两次可以看成是两条路径同时走,因此k表示两条路线当前走到的各自的横纵坐标之和k == i1 + j1 == i2 + j2
状态表示与状态计算均放在上图中
类比数组三角形模型,不难得出f[i ][j],但注意本题需要走两次,等价于从起点到终点两条完全不重复的路径,两条路径就分别有两个坐标,应该用4维数组表示,即f[i1][j1][i2][j2],但我们发现经过重复点等价于i1+j1==i2+j2所以我们可以引入变量k表示横纵坐标和。这样可以压缩一维空间。
由于题目只能向右和向下走,且有两条路径,所以方案数共有2*2=4种,将其全排列即可,也可以通过二进制表示即00,01,10,11,0表示向右,1表示向下。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 15;
int f[2*N][N][N];
int w[N][N];
int n;
int main(){
cin>>n;
int a,b,c;
while(cin>>a>>b>>c,a||b||c){
w[a][b]=c;
}
for(int k=2;k<=n+n;k++){
for(int i1=1;i1<=n;i1++){
for(int i2=1;i2<=n;i2++){
int j1=k-i1;
int j2=k-i2;
if(j1>=1&&j1<=n&&j2<=n&&j2>=1){
int x=w[i1][j1];
if(i1!=i2){
x+=w[i2][j2];
}
int& t=f[k][i1][i2];
t=max(t,f[k-1][i1][i2]+x);
t=max(t,f[k-1][i1-1][i2]+x);
t=max(t,f[k-1][i1-1][i2-1]+x);
t=max(t,f[k-1][i1][i2-1]+x);
}
}
}
}
cout<<f[n+n][n][n]<<endl;
return 0;
}
类比题目为NOIP提高组2008 传纸条,做法相同,不予分析
如果本文对您有帮助,记得点赞收藏哦~~。