可视化特征缩放（Feature Scaling）

数据分布

我们在[0,100]范围内随机生成shape=(100,100)的100个整数点，每个点就是一个样本，有两个属性a和b。

import numpy as np
import matplotlib.pyplot as plt

# 100个样本点
# data = np.random.randint(0, 200, size=[100, 100])
data = np.random.uniform(0, 200, size=[100, 100])

a = data[0]  # 属性a
b = data[1]  # 属性b
print(f"a的均值={np.mean(a):.2f}，a的方差={np.var(a):.2f}，a的标准差={np.std(a):.2f}")
print(f"b的均值={np.mean(b):.2f}，b的方差={np.var(b):.2f}，b的标准差={np.std(b):.2f}",)

ax0 = plt.subplot()
ax0.scatter(a, b, c='y')

ax0.set_ylabel('Y')
ax0.set_xlabel('X')
plt.show()

a的均值=97.39，a的方差=3069.09，a的标准差=55.40
b的均值=97.59，b的方差=2930.27，b的标准差=54.13

我们采用的是随机选择样本点，随机生成的样本点服从是均匀分布，可以看到样本点均匀的分散在图中。

然后，我们分别对属性a和b按照如下Z-Score公式进行更新：
$x=\frac{a-{\mu }_a}{{\sigma }_a}$，$y=\frac{b-{\mu }_b}{{\sigma }_b}$

x=(a-np.mean(a))/np.std(a)
y=(b-np.mean(b))/np.std(b)
print(f"x的均值={np.mean(x):.2f}，x的方差={np.var(x):.2f}，x的标准差={np.std(x):.2f}")
print(f"y的均值={np.mean(y):.2f}，y的方差={np.var(y):.2f}，y的标准差={np.std(y):.2f}")

ax0 = plt.subplot()
ax0.scatter(x,y, c='y')
ax0.set_ylabel('Y')
ax0.set_xlabel('X')
plt.show()

x的均值=0.00，x的方差=1.00，x的标准差=1.00
y的均值=0.00，y的方差=1.00，y的标准差=1.00

变更前后的散点图是一模一样的，只是其横坐标和纵坐标的范围改变了。所以任何分布都可以通过Z-Score公式将原来不为0的均值变成0，原来不为1的方差变成1。

均值为0方差为1的分布不一定是标准正态分布，而标准正态分布的均值一定为0，方差一定为1。

标准正态分布的散点图是这样的：

可以看出点是中间多两边少的特征。

特征缩放（Feature Scaling）

import numpy as np
import matplotlib.pyplot as plt

data = np.random.randint(100, 200, size=[40, 40])

a = data[0]
b = data[1]

x=np.append(a,2*a)
y=np.append(b,2*b)

x=np.append(x,0.5*a)
y=np.append(y,0.5*b)

x=np.append(x,a+100)
y=np.append(y,b)

x=np.append(x,a)
y=np.append(y,b+100)

ax = plt.subplot(111)  # 创建一个三维的绘图工程
#  将数据点分成三部分画，在颜色上有区分度
ax.scatter(x[:40], y[:40], c='y')  # 绘制数据点
ax.scatter(x[40:80], y[40:80], c='red')
ax.scatter(x[80:120], y[80:120], c='green')
ax.scatter(x[120:140], y[120:140], c='black')
ax.scatter(x[140:180], y[140:180], c='black')

ax.set_ylabel('Y')
ax.set_xlabel('X')
plt.show()

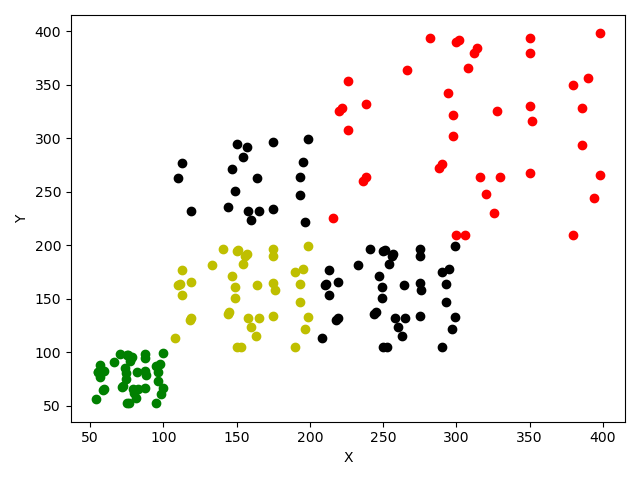
图中黄色点是原始数据（服从均匀分布），红色点=原始数据*2，是对原始数据的放大；红色点=原始数据/2，是对原始数据的缩小。可以明显看到数据的形状（即分布）没有变化，但是数据点之间的间隔（即数据的离散度）响应放大或缩小了。

黑色点是原始数据的位移（向右和向上），可以看到变化前后数据点的形状和间隔都没有变化，即其分布和方差都没变。

上图中，相对黄色点，所有变化（缩放、位移）都改变了位置，那么他们的均值都会变化。

所以特征缩放是指对样本的某一属性（或特征）进行缩放（乘除）或位移（加减）其分布并不会变化—这一特性叫做尺度不变性（Scale Invariance）。

如果我们对属性值进行特征缩放（上面的例子就是），对应的特性就是 Data Scale Invariance；
如果我们对权重值进行特征缩放，对应的特性就是 Weight Scale Invariance。

为什么我们要进行特征缩放？
目的是将样本的属性值限定在一定的范围内。

那为什么要将样本属性值限定在一定范围内呢？

from matplotlib.pylab import *

a = np.random.uniform(4, 10, size=[10])
b = np.random.uniform(0, 3, size=[10])

t = arange(-10.0, 10.3, 0.1)
s = 1/(1 + exp(-t))
ax = subplot()
ax.scatter(a, b, c='red')

ax.plot(t,s)
ax.axis([-10,10,-0.1,3.1])
plt.xlabel('x')
plt.ylabel('y')
show()

图中的Sigmoid是针对属性$x$画的。

我们有10个样本点，其$x$值范围在[4,10]，如果我们使用Sigmoid函数对其进行非线性映射，映射后最小值$y=\frac{1}{1+e^{-4}}\approx 0.98$，显然这个过程是不正常的（non-normal）或者说是非标准的（non-standard），如果我们不对数据进行处理，显然也无法进行正确建模。这时就需要对数据进行Feature Scaling了，如果我们采用Z-Score公式对样本进行缩放：

n=(a-np.mean(a))/np.std(a)
m=(b-np.mean(b))/np.std(b)

ax = subplot()
ax.scatter(n, m, c='red')
ax.plot(t,s)
ax.axis([-10,10,-2,2])
plt.xlabel('x')
plt.ylabel('y')
show()

现在样本点$x$的范围被我们限定在[-2.5,2.5]之间了，且在缩放的过程中数据分布并没有变化。这样通过Sigmoid函数非线性化才有意义，这一过程叫做正常化（normalize）或标准化（standardlize）。

FeatureScaling本质是线性($ax+b$)变化，线性变化是不改变数据分布的，而非线性变化会改变数据分布。

所以将不正常的或不标准的样本通过Feature Scaling使其正常化或标准化的过程叫Normalization或Standardization。所以Normalization和Standardization本无区别，其本质都是Feature Scaling，用的人多了就误认为他们有区别，然后一传十，十传百。

不信咱来纠正错误：
有人说：Standardization是将数据正态化，使平均值0方差为1。还给了公式x’=(x-mean)/std。这个错误很显然，如果原始样本都不是正态分布，那么通过该公式是不能变成正态化的！

将样本的属性值限定在一定的范围内的好处? = 特征缩放的好处

1、消除数据量纲对建模的影响；
2、加速神经网络的收敛（或学习）；
3、一定程度上可以解决梯度弥散（消失）或梯度爆炸问题。

Feature Scaling的方法/技术/手段

Z-score:
$$\mu =\frac{1}{n}\sum _{i=1}^n{x}_i$$
$$\sigma =\sqrt{\frac{1}{n}\sum _{i=1}^n(x_i-\mu )}$$
$${\bar{x}}_i=\frac{x_i-\mu }{\sigma }$$
其中$\mu$和$\sigma$分别是属性$x$的均值与标准差。
Z-score之后其$\bar{\mu }=0$，$\bar{\sigma }=1$

Min-Max scaling：

$${\bar{x}}_i=\frac{x_i-x_{min}}{x_{max}-x_{min}}$$
将数据限定在[0,1]之间。

Local Response Normalization

白化（Whitening）

Batch Normalization

Layer Normalization
Weight Normalization
参考Internal Covariate Shift与Normalization