Matlab符号数学（Symbolic Math with MATLAB）MATLAB解方程

创建符号变量

用符号而不是数值表示数字。

存储数字符号

% 你可以把一个数存储为数值格式，就像我们经常做的那样
x = 3;
% 你也可以把这个数存储为符号格式，使用sym()函数
xsym = sym(3);
% 数值和符号的区别在于，你定义了一个x，它的值是数字3；你用一个符号xsym来表示数字3
% 当使用数值格式存储的时候，matlab会根据它存储数字的精度，自动四舍五入
% 当使用符号格式存储的时候，他只是代表这个数字的一个符号，会保留这个数字最原始的样子
y = 2/3
ysym = sym(2/3)

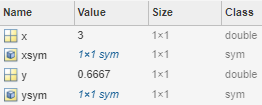
符号变量

符号变量的名字是对应于我们常用的数值变量(x=3)的。

% 使用syms命令定义符号变量
syms a b c x
% 对符号变量执行计算的输出不再是数值，而是符号表达式
x+3
x^2
sqrt(x)

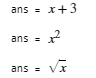
用符号变量表示数学表达式

创建符号表达式

只需要保证你所用到的变量都是符号变量就可以了。

syms x
expr = x^2+5*x+6

syms a b c
y = a*x^2+b*x+c

z = expr*pi
x = expr*4+5*y

给定义的符号变量带入值

使用subs()函数完成这一功能。v = subs(expression,variable,value)
所有可能出现的关于subs()函数的使用情况都在下面了

syms x a b c
expr = x^2 + x + 1
y = a*x^2 + b*x + c

s = subs(expr, x, 2)

ys = subs(y, a, 3)

ymult = subs(y, [a b c], [3 2 1])

subs(y, a, [1 2 3])

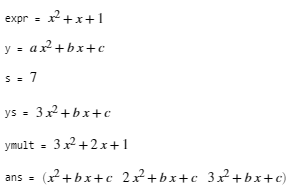
画表达式图像

可以使用fplot(expression)函数，画出表达式的图像。fplot()的使用与plot()一样。基本的使用情况都在下面给出

syms x
yLinear = (3/2)*x + 4
yCubic = x^3/8-2*x+3
fplot(yLinear)
hold on
fplot(yCubic)
hold off

定义和解符号方程

定义符号方程

使用“==”定义符号方程。

syms x
eqn = x^2-4==0	% 把x^2=0这个符号方程，存储在eqn中。

syms m v g h const
KE = (1/2)*m*v^2
PE = m*g*h
consE = KE+PE==const

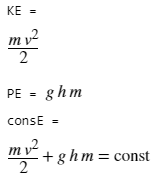
解符号方程

使用solve(equation, variable)函数，从方程equation中解出变量variable的表达式。而且还可以解方程组，使用方法见下代码。

syms x a b c
eqn = x/3 + 2 == 7	% 定义一个符号方程eqn
xsol = solve(eqn,x)	% 解这个方程中的变量x

eqn2 = x^2 - 4 == 0
xsol2 = solve(eqn2,x)	% 如果是方程有多个根，会返回一个列向量

syms a b
eqnMult = a*b == 12
eqnAdd = a + b == 7
quadsol = solve(a*x^2+b*x+c==0,x)	% 如果是方程有多个根，会返回一个列向量

[asol, bsol] = solve([eqnMult, eqnAdd], [a, b])	% 也可以解方程组
sol =  solve([eqnMult eqnAdd],[a b])	% 如果只定义一个输出，会返回一个结构体

注意：无论这个方程的解是一个数还是一个含有未知参量的表达式，这个解都是一个sym，而不是一个数值。

函数处理与化简

有一些函数可以处理变量和系数。
newexpression = expand(expression)函数能实现对函数表达式的展开。
newexpression = simplify(expression)函数能找到更简洁的表达式。
f = factor(expression)函数能够对表达式分解因子。

设置条件

规定符号变量的取值范围

使用assume(variable, assumption)函数可以规定符号变量variable的取值范围。
使用asmp = assumptions(variable)函数能够查看符号变量variable的取值范围

syms x	% 定义符号变量x
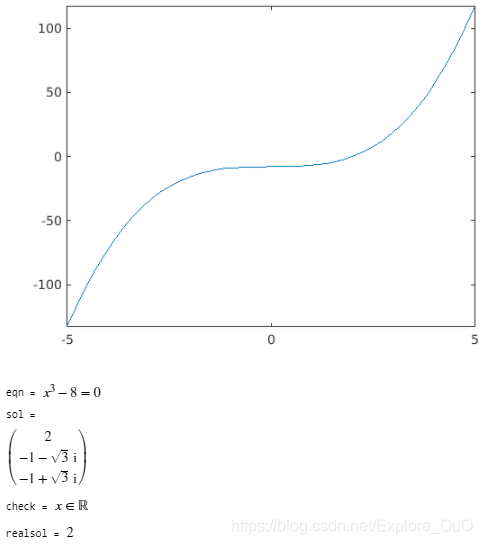
y = x^3-8;
fplot(y)	% 可以看到图像中只有一个零点

eqn = y==0
sol = solve(eqn, x)	% 而实际求解却又三个根，一个实数两个复数

assume(x, 'real');	% 将x的取值范围设置为实数
check = assumptions(x)	% 查看x的取值范围

realsol = solve(eqn, x)	% 重解x，根只剩一个实数根

% 清除对x的限制，因为只有使用assumptions函数才会显示其取值范围
% 在计算过程中并不会显示x的取值范围，所以不需要是，一定记得清除
assume(x, 'clear')	

设置多个条件

使用solve()函数可以同时对多个变量设置限定条件。使用solveAlso()函数还可以在原有限制条件上追加新的条件。

syms a b
pyth = a^2 + b^2 == 13^2
assume([a b], 'integer')
[aInt bInt] = solve(pyth, [a b])
assumeAlso([a b], 'positive')
[aPos bPos] = solve(pyth, [a b])
assumeAlso(b>a)
[aSol bSol] = solve(pyth, [a b])
assume([a b], 'clear')

使用测量单位

设置单位

Matlab支持对数据赋予单位。Matlab中有一个符号单位集合。使用u = symunit可以定义一个符号单位集合u。各单位以结构体的形式存储，如：u.mile u.hour

所以当我们定义符号变量的时候可以同时把单位也一同定义。
d = 168*u.mile
t = 4*u.hour

在对有单位的符号变量进行运算时，量纲也会一同计算
v = d/t

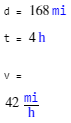
还可以使用[value, units] = separateUnits(expression)函数，将数值和量纲分离

转化单位系统

可以使用unitConvert()函数将数值在不同的量纲之间进行转换。

u = symunit
v = 42*u.mile/u.hour
vSI = unitConvert(v, 'SI')
vkph = unitConvert(vSI, u.km/u.hour)

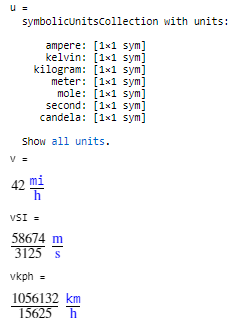
由于符号变量中存储的都是数值的精确值，可以使用double()函数实现近似值的转化。而使用double()函数时，不能够带有量纲，所以使用前一定要用separateUnits()函数把量纲分离。

创建符号函数

符号函数可以用来表示数学函数。

syms r
f(r) = pi*r^2

创建符号函数之后，对表达式代入值时，不需要再使用subs函数了。

A = f(3)	% 直接代数就行，爽的吖批

对于多变量函数，也可以只指定一个变量的值。也可以传入一个向量，符号函数会分别计算向量中每一个元素对应的函数值。

syms r
f(r) = pi*r^2
rVec = [1 2 3 5 8]
AVec = f(rVec)

syms a b
h(a, b) = pi*a*b
v = h(4, b)

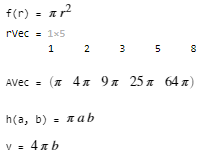
除了数值之外，还可以将符号变量和表达式作为参数传递给符号函数。输出是一个表达式。

syms x y
f(x) = x^2+4
expr = f(5*y^2)
eqn = f+3*x==7+x

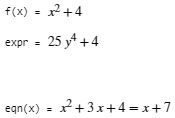
符号函数的结构是

当使用f时，他是一个symfun结构。当使用f(x)他是一个sym结构。

画函数图像

二维图像

单变量显函数画图

显函数画图的方法在上面章节以及写过了。使用fplot()函数即可。可以对符号方程 画图也可对符号函数画图。

单变量隐函数画图

隐函数可以使用fimplicit()函数画图，还可以通过fcontour()函数一次性对不同常量的同一函数画图。

syms x y
f(x,y) = x^2 + y^2
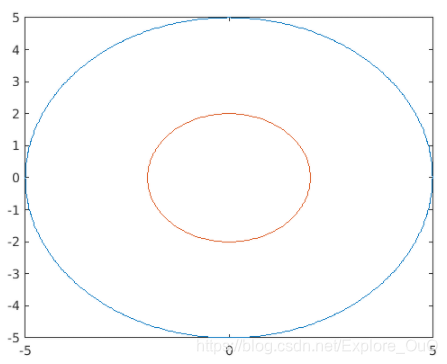
fimplicit(f==25)
hold on
fimplicit(x^2+y^2==4)
hold off

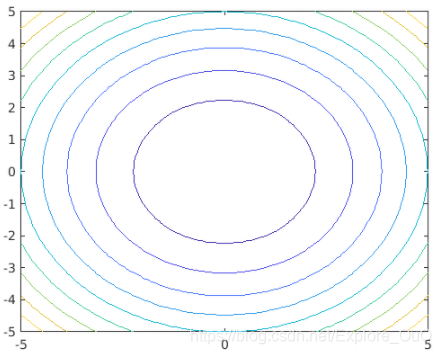
fcontour(f)
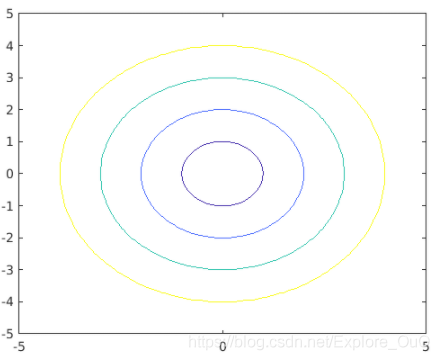
fcontour(f,'LevelList',[1 4 9 16])

三维图像

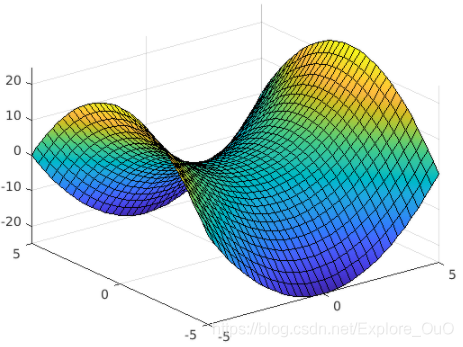
双变量显函数

显示函数用fsurf()函数，与fplot()同理。

syms x y z
f(x,y) = x^2 - y^2
fsurf(f)

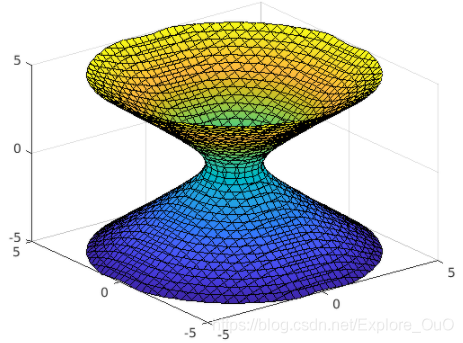
双变量隐函数

隐函数用fimplicit3()函数，与fimplicit()函数同理。

fimplicit3(x^2+y^2-z^2 == 1)

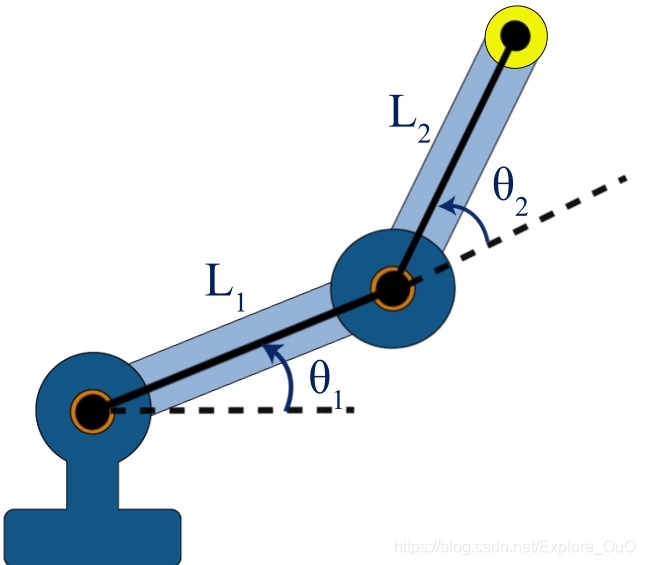
机器臂项目

Introduction to Symbolic Math with MATLAB

机械手有四个参数。两个连杆的长度是$L_1$和%L_2%，两个关节的旋转角度是${\theta }_1$和${\theta }_2$。

对应的坐标为$$x=L_{2}cos({\theta }_1+{\theta }_2)+L_{1}cos({\theta }_1)$$$$y=L_{2}sin({\theta }_1+{\theta }_2)+L_{1}sin({\theta }_1)$$

syms L1 L2 theta1 theta2

x = L2*cos(theta1+theta2)+L1*cos(theta1)
y = L2*sin(theta1+theta2)+L1*sin(theta1)

这个机器人的第一个连杆长4英尺，第二个连杆长2英尺。代入这些值将公式从4个参数减少到2个参数。

fx(theta1,theta2) = subs(x,[L1 L2],[4 2])
fy(theta1,theta2) = subs(y,[L1 L2],[4 2])

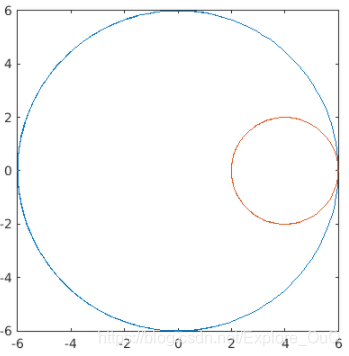
使用fplot()绘制平面图时，可以传入两个函数。但是他们他们只能有一个相同的变量。其实换汤不换药，还是保证他是一个y(x)函数就好。

fplot(fx(theta1,0),fy(theta1,0))
axis equal	% 让x和y坐标的比例相同

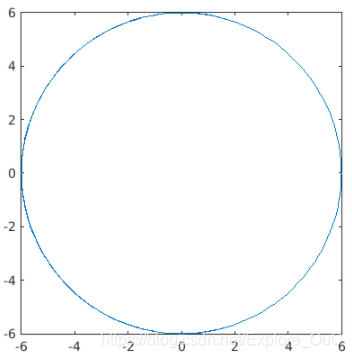
上图是对大臂范围的可视化。下面令${\theta }_1=0$可视化小臂的范围。

hold on
fplot(fx(0,theta2),fy(0,theta2))
hold off

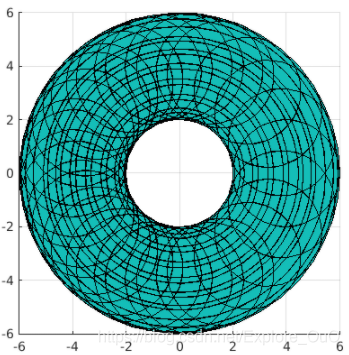
我们可以画一个z=0的三维图，可视化${\theta }_1,{\theta }_2$的所有取值得到的二维图像(其实它是个三维的，但是可以用view(2)命令使得视角只看xy平面)

fsurf(fx,fy,0)
view(2)	% 只看x-y平面
axis equal	% 规整坐标系比例

下面是一些练习

% 定义机械臂对应的符号函数
syms theta1 theta2
fx(theta1,theta2) = 2*cos(theta1+theta2) + 4*cos(theta1)
fy(theta1,theta2) = 2*sin(theta1+theta2) + 4*sin(theta1)

% 求解theta1=pi/8, theta2=pi/6时，机械臂的坐标
xpos = fx(pi/8,pi/6)
ypos = fy(pi/8,pi/6)
xposn = double(xpos)	% 输出近似值
yposn = double(ypos)
% 把theta1和theta2的范围限制在[0,pi]内，求(3,5)点对应的机械臂的两个角
assume([theta1 theta2] >= 0)
assumeAlso([theta1 theta2] <= pi)
eqx = fx==3
eqy = fy==5
[theta1sol,theta2sol] = solve([eqx eqy],[theta1 theta2])
double(theta1sol)
double(theta2sol)

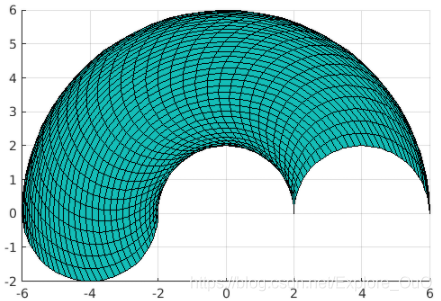
% 画一下theta1和theta2的范围限制在[0,pi]内的图
fsurf(fx,fy,0,[0 pi])
view(2)
axis equal

微积分

求导(derivatives)

用diff()函数求导。

syms x
y = 5*x^3
% 可以求导，还可以求n阶导数
dy = diff(y, x)
dy2 = diff(y, x, 2)

求积分(intergrals)

用int()函数积分。

syms x
y = 5*x^3
yint = int(y,x)
yArea = int(y,x,[0 3])

多变量函数的微分(differentiating)和积分(integrating)

一个骚操作就是可以混合求导，先对x求导再对y求导。

syms x y
expr = 3*x^2 + 2*x^2*y^2 - y^2
diff(expr,x,y)

使用泰勒多项式逼近函数

泰勒多项式在一个已知值附近，近似一个函数。你可以在附近点计算多项式来得到函数的近似值。

syms x
g(x) = exp(x-1)
p = taylor(g, x, 1)	% 对函数g(x)在x=1处做泰勒展开

默认返回一个最高次方为5的多项式。

p9 = taylor(g,x,1,'Order',10)	% 返回最高次方为10-1=9的多项式

double(g(1.5) - p(1.5))
double(g(1.5) - p9(1.5))

可以看到近似度很高。

解常微分方程

微分方程是包含因变量和自变量的方程，其中方程包含因变量的导数。

% 定义一个差分方程
syms y(x)
deqn = diff(y,x)==2*x+4*y

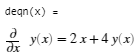
% 解这个微分方程
ysol = dsolve(deqn)

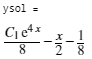
注意这个常数出现在解的指数旁边,微分方程对任意常数值都成立。如果知道y(x)的一个对应关系就可以确定这个常数值。这个附加的约束通常称为初始条件。

ic = y(0) == -1	% 初始条件

对于具有初始条件的微分方程，可以采用以初始条件为第二输入的dsolve()函数进行求解。

yp = dsolve(deqn,ic)

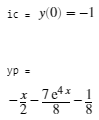
蹦极项目

高空弹跳用一根长橡皮绳绑在跳者身上。当一个人跳的时候，绳子就会不断延伸，减缓跳楼者的下降速度。跳投者减速停止，然后向上反弹。跳跃者上下摆动，直到动能消散，在一个平衡位置上静止。

蹦极的一个简单模型是质量-弹簧-阻尼系统。将蹦极者模型为质量m，将蹦极绳模型为弹簧(弹簧常数k)，将能量耗散模型为阻尼器(阻尼系数b)。

在这个项目中，你将模拟蹦极作为一个质量-弹簧-阻尼系统。

y(t):从平衡位置(m)
m:蹦极者质量(kg)
b:阻尼系数(s/m)
k:弹簧常数(N/m)

% 将位置、阻尼系数、弹簧常数定义为符号变量。将体重定义为数值变量。
syms y(t) b k
m = 75;
% 这些变量代表物理量，是实值不是虚值。弹簧常数k和阻尼系数b是正实的。
assume(y(t),'real')
assume([b k],'positive')
% 用微分方程模拟质量-弹簧-阻尼系统(蹦极系统)
bungeeEqn = m*diff(y,t,2)+b*diff(y,t)+k*y==0
% 蹦极绳的平衡高度是75米，在起跳时比平衡高度高出75米。
ic = y(0)==75
% 在跳跃的开始，初始速度是零。
% 可以先将导数存储为函数，然后定义初始条件，从而为导数创建初始条件。
dy(t) = diff(y(t))
ic2 = dy(0) == 0

你已经用一个二阶微分方程和两个初始条件模拟了蹦极。接下来，你将解微分方程，并想象随着时间的推移蹦极者的高度。

% 初始位置存储在ic中，初始速度存储在ic2中。
% dsolve()函数可以求解具有多个初始条件的微分方程。
ysol = dsolve(bungeeEqn,[ic ic2])

%解决方案取决于参数b和k。为了绘制解决方案，您将需要替换这些参数的值。
yequil = subs(ysol,[b k],[4 8])
fplot(yequil,[0 150])

这张图显示了蹦极者相对于平衡的位置。要绘制蹦极者相对于地面的高度，您可以对函数应用位移。
蹦极绳的平衡长度为75米，桥的高度为152米。所以蹦极者在离地面77米的地方保持平衡。

ygnd = yequil + 77
fplot(ygnd,[0 150])

你已经将蹦极建模为一个质量-弹簧-阻尼系统，并绘制了蹦极者随着时间的推移的高度。
你怎样才能知道蹦极者所走的总距离呢?走过的总距离就是曲线的长度。

曲线z(t)的长度公式如下$$L{\int }_a^b\sqrt{1+(\frac{dz}{dt}{)}^2}dt$$
要计算蹦极者在跳跃的前100秒内所走的总距离，可以使用int来计算从0到100的积分。

d = sqrt(1+(diff(yequil,t))^2)
L = int(d,0,100)
double(L)