题意:给你一个正整数n,你有k次操作,每次操作n除以一个n的因数(1-n均可),除以任意一个的概率相同,求最后留下来的数字的数学期望。(1<=n<=10^15,1<=)
范围:分治、逆元、dp(找规律??)
注意:楼主不敢保证思路正确,希望大佬看到对于一些不当见谅,如果能帮指正下,那万分感谢
思路:首先看完题意,草稿纸模拟一遍,再看看数据范围,woc这题什么鬼,然后开始自闭。
没错比赛时就是这样度过的。
。。。。。。
言归正传(叹气),这题怎么写呢,首先和因数有关,那么就从这个角度入手,全部同时考虑肯定会炸,只好先看看只有一个质因数的情况。
比如2:i[] = 1 2 4 8;
显而易见,每一个数的因数数量等于小于等于本身的数的数量m = log2(i[a]) + 1,而在每次操作后,假设原在该值得概率为j[a],每个因数就分配到j[a]/m;
接下来看看分裂次数造成得影响;
| 1 | 2 | 4 | 8 | |
|---|---|---|---|---|
| 1 | j[1] | |||
| 2 | j[2]/2 | j[2]/2 | ||
| 4 | j[3]/3 | j[3]/3 | j[3]/3 | |
| 8 | j[4]/4 | j[4]/4 | j[4]/4 | j[4]/4 |
| sum |
横行表示旧的每个值对新的每个值的影响,纵行表示每个新的值及各个值,如果把每个值加到一起,用下面的sum记录,就是新的值。
通过这个表就可以推出只有一个质因数时每次分裂后值的变化,用前缀和从后往前优化下,时间复杂度就在允许范围内了。
这只是一个质因数的情况,那么来推多个的 (以下可能出现不完全正确,语音组织不佳的情况)
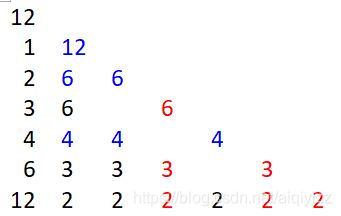
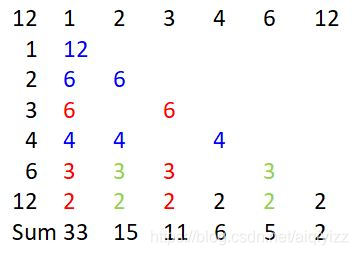
还是举个例子:12,又我们知道,在第一次操作时,所有该数的因数都为等概率,我假设都为1,还有为计算方便,所有概率乘以一个分母的最小公倍数,可得如下表:
| 1 | 2 | 3 | 4 | 6 | 12 | |
|---|---|---|---|---|---|---|
| 1 | 12 | |||||
| 2 | 6 | 6 | ||||
| 3 | 6 | 6 | ||||
| 4 | 4 | 4 | 4 | |||
| 6 | 3 | 3 | 3 | 3 | ||
| 12 | 2 | 2 | 2 | 2 | 2 | 2 |
可以尝试猜想一下,只有一个质因数得出来的结果和多个质因数是否有关系?
单纯仅看1 2 4的数据,是符合单个质因数推出的情况;
那么将它分成两部分:{1,2,4},{3,6,12}。
从上面这张图蓝色部分为红色部分的2倍,这里2倍的原因是以上i[a]的因数个数是3i[a]的一半,3i[a]一半在红,一半在黑。
纵方向,这张图每种非蓝色为上方各蓝色的1/2;横的方向,同种颜色数值相等。
计算可得{1,2,4}与{3,6,12}符合3:1(只有一个质因数,质因数出现次数为1,操作次数为2)的关系。
为什么一定是3:1?上面已证出。
为什么出现3:1?因为质因数3出现次数为1,操作次数为2。
那么出现次数为2及以上的是否符合?是的,读者可以自行推导下,步骤如上二图(可能要注意一图的蓝色、红色部分选取)。
因此,设res(n,m)是答案,tim是因数p在n中次数,那么res(n*p,m)=res(n,m)*res(p^(tim+1),m)/res(p ^tim,m)。从这式子可以看出,答案只受与这个质因数相关系的结果。整理一下,就是每个因数可以单独算出单个因数的影响,然后相乘得出结果。
可以预处理出单个因数的影响,不过不预处理影响不大,因为数据范围内,质因数总数不会多。
代码如下:
#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const ll Mod = 1e9 + 7;
int inv[maxn];
void invers(int o)
{
inv[1] = 1;
for(int oo = 2;oo <= o;oo ++)
{
inv[oo] = (long long)(Mod - Mod / oo) * inv[Mod % oo] % Mod;
}
}
ll ce(ll o,ll onum,ll kk)
{
ll arr[onum + 1][2],o1=0,o2=1;
arr[onum][0] = 1;
for(ll pp = 0;pp < onum;pp ++) arr[pp][0] = 0;
for(ll pp = 1;pp <= kk;pp ++)
{
for(ll oo = onum;oo >= 0;oo --)
{
arr[oo][o2] = arr[oo][o1] * inv[oo + 1] % Mod;
if(oo != onum) arr[oo][o2] = (arr[oo][o2] + arr[oo+1][o2]) % Mod;
}
swap(o1,o2);
}
ll p = 1;
ll ress = arr[0][o1];
for(ll oo = 1;oo <= onum;oo ++)
{
p = p * o % Mod;
ress = (ress + arr[oo][o1] * p % Mod) % Mod;
}
return ress;
}
ll n,k,a,res;
int main()
{
scanf("%I64d%I64d",&n,&k);
invers(100000);
res = 1;
for(a = 2;a * a <= n;a ++)
if(n % a == 0)
{
int anum = 0;
while(n % a == 0)
{
anum ++;
n /= a;
}
if(anum != 0)
res = res * ce(a,anum,k) % Mod;
}
if(n != 1)
res = res * ce(n,1,k) % Mod;
printf("%I64d\n",res);
return 0;
}