2019.05.25 【NOIP提高组】模拟 A 组 比赛总结

题目

小a的强迫症

Description

Input

Output

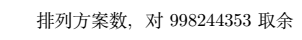
Sample Input

3
2 2 1

Sample Output

3
样例解释：

Data Constraint

---

数格子

Description

Input

Output

Sample Input

1 10000
3 10000
5 10000
0 0

Sample Output

1
11
95

Data Constraint

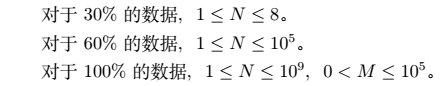
Hint

每个测试点数据组数不超过10组

---

序列

Description

Input

Output

Sample Input

1
5
2 1 3 0 3
2 2 0 1 0

Sample Output

1

Data Constraint

---

总结

这次比赛非常差，搞了老半天只有0分。
先是觉得T2最可做，想起以前解决2*N的矩阵填充的递推问题，感觉这题也是类似的，于是推式子。我发现每一列只有5种可行的形状：（假设前面的列全部都填满了，浅颜色为什么都不填，深颜色为已填充）
第一种：
░░░░
第二种：
░░██
第三种：
░██░
第四种：
██░░
第五种：
█░░█
然后发现两行间不同状态间的转移状态（只要加方块可以达到都可以），结果算了一堆重复状态，就GG了。
于是回到T1，我以为算出每种颜色最后一个珠子的放置方案数就可以了。心想：这题怎么这么简单？
式子显然为${\prod }_{i=1}^{n}1+{\sum }_{j=i+1}^n{a}_i-1$。
结果连样例也过不了（其他珠子的放置方案也是很多的）
当然，即便我算出了正解，也AC不了，因为我不会矩阵乘法。
最后绝望地看T3，总觉得是差分，但是我不知道怎么解决集体+4的情况，对差分理解不深入，于是0分。

---

题解

T1

其实可以理解为一种一种颜色地放珠子。
那么每一种颜色（除第一种外）都有1个珠子被固定（放在最后一位），其他珠子的方案数就是$C_{a_i-1}^{sum-1}$,其中$sum={\sum }_{i=1}^n{a}_i$。
最后答案乘起来就可以了。

T2

设$f_{i,j}$表示第 i 列的放置情况为 j（状压），第1~i-1列全部都被填满了。
状态转移方程显然。
但是n是$10^9$级别的，因此要用优化。由于每一层的转移其实都是一样的，所以可以用矩阵乘法。
问题在于如何构造矩阵。
注意到矩阵乘法的方式是这样的：$$c_{i,j}=\sum _{k=1}^n{a}_{i,k}\times b_{k,j}$$
由于这里的 f 数组的每一列状态都是一维的，因此我们可以变为一个一维矩阵乘以一个二维矩阵：$$c_i=\sum _{j=1}^n{a}_j\ast b_{j,i}$$
因此，可以用$b_{i,j}$表示 i 状态是否能够转移到 j 状态。
这样矩阵就构造出来了。

T3

显然是差分。
先计算出每一个数至少需要增加多少次（用a表示）。考虑一段区间加的情况，最容易想到把区间[l…r]加上${\min }_{i=l}^r{a}_i$。但是有的时候把一些数+4，再把2个区间合并起来可能会更优。
这时候这个时候整体+4的区间[i…j]内的其他数字都不会受影响，除了 i 和 j。
当这样更优时，是满足一个性质的：$$a_{i-1}-a_i>a_j+4-a_{j+1}$$
这时它对答案的贡献就是$a_{i-1}-a_i$。
先统计答案，再判断这种情况就可以了。

---

CODE

T1

#include<cstdio>
using namespace std;
#define ll long long
#define mod 998244353
#define exp 998244351
#define N 100005
#define M 500005
ll a[N],f[M],g[M],n,ans,sum,i;
inline ll pow(ll x,ll y)
{
    
    
	ll s=1;
	while(y)
	{
    
    
		if(y&1) s=s*x%mod;
		x=x*x%mod,y>>=1;
	}
	return s;
}
inline ll C(ll x,ll y){
    
    return f[x]*g[y]%mod*g[x-y]%mod;}
int main()
{
    
    
	scanf("%lld",&n);
	for(i=1;i<=n;i++) scanf("%lld",a+i);
	sum=a[1],ans=f[0]=g[0]=1;
	for(i=1;i<M;i++) f[i]=f[i-1]*i%mod,g[i]=pow(f[i],exp);
	for(i=2;i<=n;i++)
	{
    
    
		sum+=a[i];
		ans=ans*C(sum-1,a[i]-1)%mod;
	}
	printf("%lld\n",ans);
	return 0;
}

T2

#include<cstdio>
#include<cstring>
using namespace std;
#define N 100005
long long m,h[16][16],f[16][16],a[16][16],t[16][16];
bool b[2][4];
inline void pow(long long x)
{
    
    
	long long i,j,k;
	while(x)
	{
    
    
		if(x&1)
		{
    
    
			memset(t,0,sizeof(t));
			for(i=0;i<16;i++)
				for(j=0;j<16;j++)
					for(k=0;k<16;k++)
						t[i][j]=(t[i][j]+a[i][k]*h[k][j]%m)%m;
			for(i=0;i<16;i++)
				for(j=0;j<16;j++)
					a[i][j]=t[i][j];
		}
		x>>=1;
		memset(t,0,sizeof(t));
		for(i=0;i<16;i++)
			for(j=0;j<16;j++)
				for(k=0;k<16;k++)
					t[i][j]=(t[i][j]+h[i][k]*h[k][j]%m)%m;
		for(i=0;i<16;i++)
			for(j=0;j<16;j++)
				h[i][j]=t[i][j];
	}
}
int main()
{
    
    
	long long n,i,j,k;
	for(i=0;i<16;i++)
	{
    
    
		for(j=0;j<16;j++)
		{
    
    
			for(k=0;k<4;k++)
				b[0][k]=((i&(1<<k))==0),
				b[1][k]=((j&(1<<k))!=0);
			for(k=0;k<4;k++)
			{
    
    
				if(b[0][k]&&b[1][k]) b[0][k]=b[1][k]=0;
				else if(k<3&&b[0][k]&&b[0][k+1]) b[0][k]=b[0][k+1]=0;
			}
			for(k=0;k<4;k++)
				if(b[0][k]||b[1][k])
					break;
			if(k>3) f[i][j]=1;
		}
	}
	while(scanf("%lld%lld",&n,&m),n|m)
	{
    
    
		for(i=0;i<16;i++)
		{
    
    
			for(j=0;j<16;j++)
				h[i][j]=f[i][j],a[i][j]=0;
			a[i][i]=1;
		}
		pow(n);printf("%lld\n",a[0][0]);
	}
	return 0;
}

T3

#include<cstdio>
using namespace std;
#define N 100005
short a[N];
int f[9];
int main()
{
    
    
	int t,n,ans,i,j;
	scanf("%d",&t);
	while(t--)
	{
    
    
		scanf("%d",&n);
		for(i=1;i<=n;i++) scanf("%hd",a+i);
		for(i=1;i<=n;i++) scanf("%d",&j),a[i]=(j+4-a[i])%4;
		f[0]=f[1]=f[2]=f[3]=f[4]=f[5]=f[6]=f[7]=f[8]=0;
		for(i=n,ans=a[n];i>1;i--)
		{
    
    
			f[a[i]+4-a[i+1]]++;
			for(j=1;j<a[i-1]-a[i];j++) if(f[j]) f[j]--,a[i]+=4,ans+=j;
			if(a[i-1]-a[i]>0) ans+=a[i-1]-a[i];
		}
		printf("%d\n",ans);
	}
	return 0;
}