【P5659】CSP-S Day1T3 树上的数（tree）题解

题目

Time Limits: 2000 ms
Memory Limits: 262144 KB

Description

Input

Output

输出到文件 tree.out 中。
对于每组测试数据，输出一行共 n 个用空格隔开的整数，表示最优操作方案下所能得到的字典序最小的 Pi。

Sample Input

4
5
2 1 3 5 4
1 3
1 4
2 4
4 5
5
3 4 2 1 5
1 2
2 3
3 4
4 5
5
1 2 5 3 4
1 2
1 3
1 4
1 5
10
1 2 3 4 5 7 8 9 10 6
1 2
1 3
1 4
1 5
5 6
6 7
7 8
8 9
9 10

Sample Output

1 3 4 2 5
1 3 5 2 4
2 3 1 4 5
2 3 4 5 6 1 7 8 9 10

Data Constraint

---

题解

这道题目质量非常高。虽然它的算法并不难，要想出来却十分有难度；即便是想出来了，也很难实现。就算你说考场上要求不高，能水点分就好了，也会发现它的链和菊花的情况十分恶心（读入也是极其恶心的，除了对正解方便之外）。
这题很显然不是DP或递推什么的东西（你把状态给我表示出来试试），因此考虑贪心。
最直接的想法就是每次从1到n枚举一个数字，然后找出它能交换到哪一个编号最小的节点。这个东西可以$n^2$来弄，总的时间复杂度就是$O(n^3)$的了。
考虑怎么优化寻找一个数能交换到哪里的过程。其实我们只要记录下边的先后关系就好了。
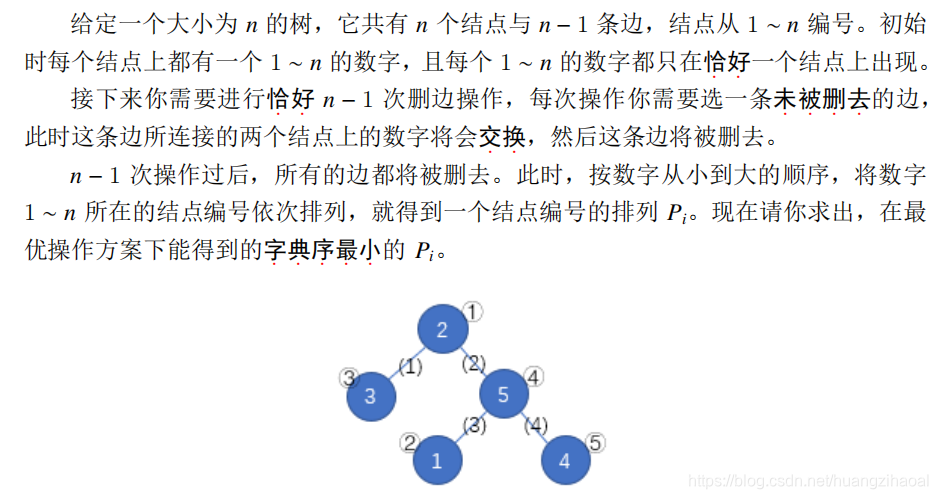
假如我们要操作下图（边权表示边的编号，点权表示点的编号，图上没有题目中“节点上数字”）：

容易发现边有一下关系：

1. ①到④中的每一个条边一定都是先后删去的，且一定是按1,2,3,4的顺序删去的；
2. ①中的其它边5,6一定要在1之后被删去；
3. ⑤中的其它边9,8一定要在4之前被删去。

这些关系比较复杂，要处理好煞是困难。但是S大佬想出了一个极其神奇的方法（假定当前从①交换到⑤）：

• 对于每一个节点，我们都建一个图，表示点的出边的对应关系。其中一条边x->y表示x是y的前一条被删去的边，图上的每一个节点都最多只有一条出边、一条入边，即这一个图是一条连通的链。此外，还要记录每一个点的图中，第一条和最后一条被删去的边（这里的第一条和最后一条指的是一切都处理完后，即程序运行完后，这个点的图上的第一条边和最后一条边）。
• 把连接起点的边标记为起点的第一条边，即把1标记为①的第一条边（在此之前①的第一条出边一定不存在）。
• 把连接终点的边标记为终点的最后一条边，即把4标记为⑤的最后一条边（在此之前⑤的最后一条出边一定不存在）。
• 经过的其他的点中，连接其相邻的两条边，即在②的图中连一条1->2的边，在③的图中连一条2->3的边，在④的图中连一条3->4的边。
• 每一次我们枚举一个数字，从它所在的节点出发，每次走到一个相邻的点，要求经过的边之间的关系不违反已经定下的先后关系（即在关系图中不能存在反向边、环、首尾直接相连但是图中并没有包含所有边等情况）。
• 总的时间复杂度就是$O(n^2)$，比暴力方法优秀了一个$n$的时间复杂度。

这样子做就可以了，但是可以发现实现起来相当复杂。以下有一些Tips：

1. 不用记录每一个数字交换到哪里（其实你也记录不了），每次只考虑一个数字的移动，只需从初始位置出发即可；
2. 寻找合法终点时，不合法的情况很多，可以分这个点是起点、中间点或终点的三种情况处理。

---

代码

#include<cstdio>
using namespace std;
#define N 2005
struct node
{
    
    
	int nex,las;
	inline void clear(){
    
    nex=las=0;}
}link[N][N];//bool print;
int st[N],ans[N],ed[N],id[N],fir[N],to[4005],nex[4005],f[N][N],pre[N],a[N][N],list[N],cnt[N],siz[N][N],deg[N],s;
inline void inc(int x,int y)
{
    
    
	++deg[x],++deg[y];
	to[++s]=y,nex[s]=fir[x],fir[x]=s;
	to[++s]=x,nex[s]=fir[y],fir[y]=s;
}
inline int getfather(int i,int k)
{
    
    
	if(f[i][k]==k) return k;
	return f[i][k]=getfather(i,f[i][k]);
}
inline void add(int k,int x,int y)
{
    
    
	link[k][x].nex=y,link[k][y].las=x;
	int fa=getfather(k,y);
	f[k][fa]=getfather(k,x);
	siz[k][f[k][x]]+=siz[k][fa];
	//printf("graph\t%d:\t%d\t->\t%d\n",k,x,y);
}
void dfs(int k,int las)
{
    
    
	for(int i=fir[k];i;i=nex[i])
		if(i>>1!=las&&(link[k][las].nex==i>>1||getfather(k,las)!=getfather(k,i>>1)&&
			!link[k][las].nex)&&(link[k][i>>1].las==las||!link[k][i>>1].las))//作为中间经过的点的情况
		{
    
    
			if(las==0&&f[k][i>>1]==getfather(k,ed[k])&&
				siz[k][f[k][i>>1]]<deg[k]) continue;//作为起点的情况
			if(st[k]&&ed[k]&&f[k][las]==st[k]&&getfather(k,ed[k])==f[k][i>>1]&&
				siz[k][st[k]]+siz[k][f[k][i>>1]]<deg[k]) continue;//作为终点的情况
			if(to[i]<s&&ed[to[i]]==0&&(i>>1!=st[to[i]]||deg[to[i]]==1))
			{
    
    
				//if(print) printf("\tprint:\t%d\n",to[i]);
				if(getfather(to[i],i>>1)==st[to[i]])
				{
    
    
					if(siz[to[i]][st[to[i]]]==deg[to[i]]) s=to[i];
				}
				else s=to[i];
			}
			pre[to[i]]=k,cnt[to[i]]=cnt[k]+1;
			dfs(to[i],i>>1);
		}
}
int main()
{
    
    
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	int t,n,i,j,x,y;
	scanf("%d",&t);
	while(t--)
	{
    
    
		scanf("%d",&n),s=1;
		for(i=1;i<=n;++i)
		{
    
    
			fir[i]=st[i]=ed[i]=deg[i]=0;
			for(j=1;j<=n;++j) link[i][j].clear(),f[i][j]=j,siz[i][j]=1;
		}
		for(i=1;i<=n;++i) scanf("%d",id+i);
		for(i=1;i<n;++i)
		{
    
    
			scanf("%d%d",&x,&y);
			a[x][y]=a[y][x]=i,inc(x,y);
		}
		for(i=1;i<=n;++i)
		{
    
    
			for(j=1;j<=n;++j) pre[j]=cnt[j]=0;
			s=N,x=id[i],cnt[x]=1;
			dfs(x,0),y=s,printf("%d ",s);
			for(j=y;j;j=pre[j]) list[cnt[j]]=j;
			//printf("%d\t%d\t%d\nlist:\t",i,x,y);
			//for(j=1;j<=cnt[y];++j) printf("%d\t",list[j]);puts("");
			//printf("graph\t%d:\tst=\t%d\n",x,a[x][list[2]]);
			//printf("graph\t%d:\ted=\t%d\n",y,a[y][list[cnt[y]-1]]);
			st[x]=a[x][list[2]],ed[y]=a[y][list[cnt[y]-1]];
			link[x][st[x]].las=N,link[y][ed[y]].nex=N;
			for(j=2;j<cnt[y];++j)
				add(list[j],a[list[j-1]][list[j]],a[list[j]][list[j+1]]);//puts("\n");
		}
		puts("");
	}
	return 0;
}