以下内容笔记出自‘跟着迪哥学python数据分析与机器学习实战’,外加个人整理添加,仅供个人复习使用。
支持向量机要解决的问题
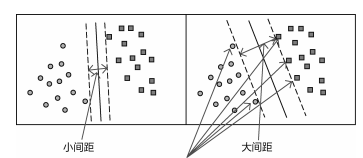
找到最好的一个决策方程,将两类数据点分离,支持向量机是不只找到决策方程,还要找到最好的一个。如图:左边的决策边界最窄,而中间决策方程的决策边界最宽,因此最好的决策方程为中间。
选择最宽的决策边界,因为这样容错能力更强,效果最好。
距离和标签定义
强调决策边界越宽越好,需要用到点到决策面距离的定义。
假设平面方程wTx+b=0,平面上有x’,x’’两个点,W为平面的法向量,要求x点到平面h的距离。现在有wTx‘+b=0,wTx’‘+b=0
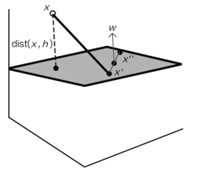
直接计算x到平面的距离较困难可以先得到x到x’的距离,再投影到平面的法向量方向上:
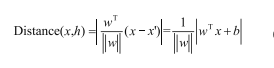

已知距离计算公式情况下,定义数据集(X1,Y1)(X2,Y2)…(Xn,Yn),其中Xn为数据特征,Yn为样本标签。当Xn为正例时,Yn=+1;大概Xn为负例时,Yn=-1。这样定义是为了之后化简做准备(就如逻辑回归中定义类别为0和1,是为了化简)。
最终的决策方程为(有监督问题):
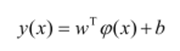
目标是求解其中的参数,其中φ(x)表示对数据进行了某种变换,我们之后再讨论。
现在我们要关注的是,对于任意输入样本数据x,有:
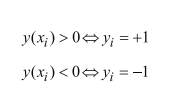
因此:
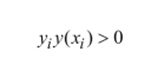
与逻辑回归推理过程有点类似,这里就体现出将标签Y定义成+1与-1的目的了,主要是用于完成化简。
目标函数
我们需要找到最佳决策方程,也就是得出最佳参数w、b.
这里要优化的目标是使得离决策方程最近的点,能够越远越好(决策带越宽越好)。
经过上面推导,已知了点到边界距离的定义:
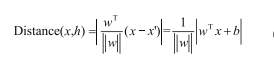
(特点是带有绝对值,不易用于计算)
而我们也已知:
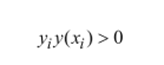
由于标签值为-1或+1,才有了yi¬y(xi)>0,也就是恒为正,那么我们可以将第一个带有绝对值的式子乘上y,以达到去掉绝对值的目的。
距离公式转换如下:
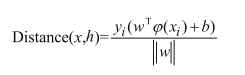
依据优化思想,推导出目标函数为:
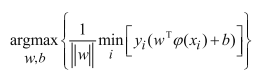
(首先min表示找到离决策边界最近的点(距离最小),argmax表示找到最合适的决策边界(w和b),使其离这个样本点的距离越大越好)。
目标函数进一步推导
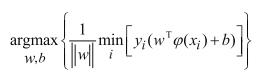
目标函数还是较为复杂,先进行化简
通过伸缩变换,由
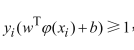
可得:
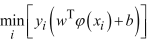
其最小值为1.
那么现在新的目标函数为:
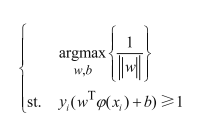
求解极大值问题,机器学习中常规套路是转化为极小值问题,因此有:
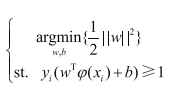
我们的目标是通过计算极值求解最佳参数w、b,但极值具体是多少关系的,所以为了方便计算,可以对公式加入某些常数项或进行某些函数变换,保证极值点不变即可。
求解目标函数
计算有约束条件函数的极值优化问题,常用拉格朗日乘子法。
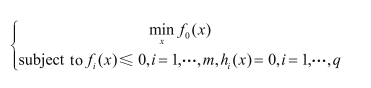
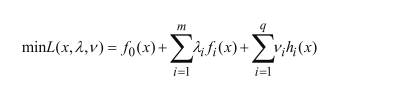
依据以上思想,将支持向量机的目标函数进行拉格朗日乘子转换:
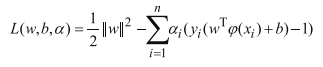
插播一个细节,KKT条件(知道有但可以不深究)
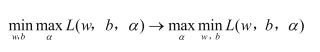
那么在我们的条件中,目标函数求极小值,即等式左边。求导后,带入拉格朗日函数,可将w和b全部替换成与a的关系,这时用到了右边等式。如下。
继续进行拉格朗日求解:
对参数求偏导:
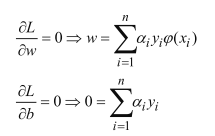
将上述方程带入拉格朗日乘子转换后的函数:
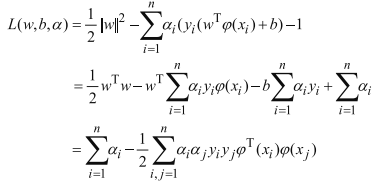
此时转化为了关于a的式子,我们需要求解:
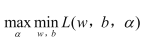
即a值为多少时,L(w,b,a)值最大,仍旧是求极大值问题,按照套路转换为极小值:
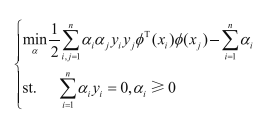
约束条件中,前一部分是拉格朗日函数对b求偏导得出的,a>=0则是拉格朗日乘子法自身的限制条件。至此,支持向量机的基本数学推导完成。
支持向量机手算例子
我们举一个只有3个样本点的例子,便于计算和化简。
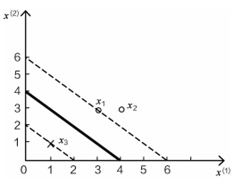
三个样本点,正例x1(3,3),x2(4,3),负例x3(1,1)
首先,将3个样本点带入:
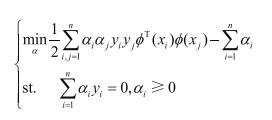
只有3个样本点,且样本标签已知:
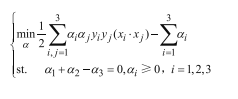
这里暂时φ(x)=x,(xi * xj)为求内积(注意是向量内积),将3个样本点和条件a1+a2-a3=0带入上式可得:
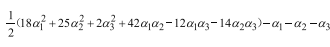
将a3=a1+a2带入:
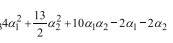
这里需要求极小值,上式分别对a1,a2求偏导,并令偏导为0,可得a1=1.5,a2=-1.但这里a出现了负数,因此需要考虑边界上的情况,即a1=0或a2=0,分别带入的:
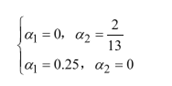
分别计算当a1=0或a2=0情况下的极值,可知当a1=0.25,a2=0时,取得最小值,此时a3=a1+a2=0.25.
在已经求解出来的a基础上,回顾之前在最初求解拉格朗日函数偏导时得出的关于w,b,a之间的式子:
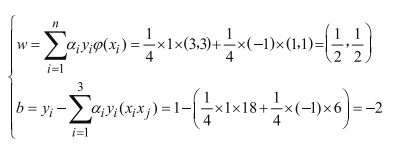
即最终的决策方程为:
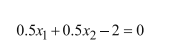
支持向量机松弛因子
由以上分析可知,权重采纳数w的结果由a,x,y决定,其中x,y分别是数据和标签,是不变的,如果求解出ai=0,意味着当前这个数据点不会对结果产生影响,因为和x,y相乘后的值还是0,只有ai不为0,对应的数据点才会对结果产生作用。
由以上推导可知:
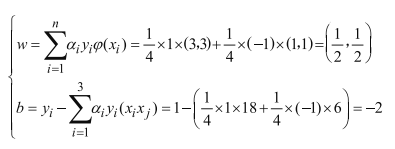
由于a2=0,在计算w的过程中,x2点没有发挥作用,对比图形:
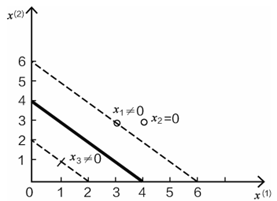
x1,x3都是边界上的点,x2为非边界点。这些边界点是影响决策方程位置的主要因素。称为支持向量。
支持向量及调参
软间隔
在一些情况下,模型为了满足个别数据点做出较大牺牲,而这些数据点可能是离群点、异常点,这是如果要求模型做到严格分类,结果并不好。会造成过拟合问题。
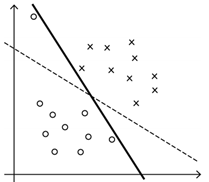
因此可一定程度上降低要求。
最开始时,我们将y设置为-1或+1,通过伸缩变换,有目标函数:
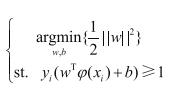
现在可加入松弛因子,即:
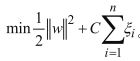
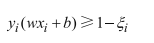
相当于放低要求,目标函数加上一部分与正则化惩罚的原理类似,用控制参数C表示严格程度。目标与之前一致,还是要求最小值。
- 当C趋于无穷大,只有让松弛因子ζ非常小,才能使整体达到极小值。意味着与之前的要求差不多,让分类十分严格,不能产生错误;
- 当C趋于无穷小时,即便ζ大一些也没关系,意味着O型可以有更大的错误容忍度,要求放低。
此时拉格朗日乘子法:
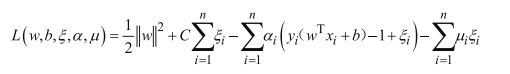
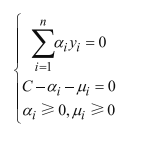
化简得:
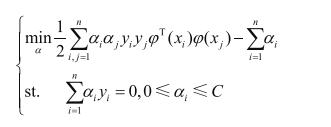
通过加入松弛因子,可以防止过拟合,比较重要!!
支持向量机核函数
在之前推导过程中的 φ(x) ,就是核函数。
我们知道可以通过对高维数据降维来提取主要信息,降维的目的是找到更好的代表特征。那么数据能不能升维呢?低维的数据信息较少,能不能利用高维的数据信息来解决低维中不好解决的问题?这就是核函数要完成的!!
这里低维不好解决的问题是什么?即低维不可分,但通过核函数能够将低维数据升维,达到高维可分的目的。
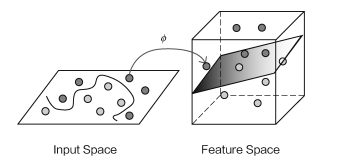
但有一点,如果数据维度大幅提升,对计算的要求自然更苛刻,在之前的求解中,计算需要考虑到所有的样本,计算内积十分麻烦,这是否大大增加求解难度呢?
比如,如果有x1=(1,2,3),x2=(4,5,6),假设在三维空间中不能实现线性划分,使用函数变换:
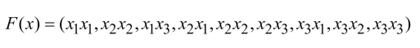
将数据射到九维空间,这时F(x1)=(1,2,3,2,4,5,3,6,9),F(x2)=(16,20,24,20,25,36,24,30,36),求解过程的计算量主要在内积上,(F(x) , F(x2))=16+40+72+40+100+180+72+180+324=1024.
上述过程在数据样本及数据维度很大时,将非常麻烦,我们发现,先在低维空间中进行内积计算,再把结果映射到高维中,得到的数值相同,K(x1,x2)=((x1 , x2))2=(4+10+18)2=1024
由此可见,有:
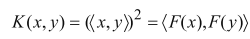
但先计算内积再映射到高维,比先映射到高维再进行内积要简单!
这里是用核函数将低维转化到了高维,但计算的时候,依旧在低维中,只是将低维的内积结果映射到了高维。(十分巧合,既利用核函数得到了更多的特征信息,也没有增加复杂度,很好地解决了低维线性不可分的问题!)
经常使用高斯核函数:(一般都选择高斯核函数)
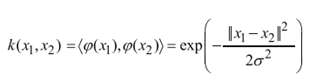
白话理解就是拿到原始数据后,先计算两两样本的相似程度,然后用距离的度量表示数据特征,如果数据相似,结果为1,否则为0.
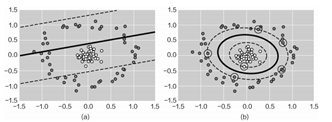
如下为线性不可分的数据集,加入高斯核函数进行变换后,原本复杂的数据能够被分开。