Fibonnacci 之 矩阵快速幂

斐波那契数列 习题

1.矩阵快速幂 推导 fibonnacci

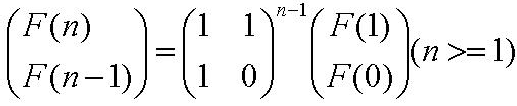
   {1        1}                                 { A     B}
   {1        0}  的n-1次方的结果设为              {C      D}

利用矩阵乘法， 可以得到 F【n】=A* F[1 ] + B* F[ 0 ]

接下来 考虑 矩阵的n-1 次方 计算，使用矩阵快速幂`

/*===================================*/
|| 快速幂（（（quickpow）））模板 ）模板 
|| P 为等比，，，I 为单位矩阵
|| MAX 要要要初始化！！！！
||
/*===================================*/
/*****************************************************/
#include 
const int MAX = 2; 
typedef struct{ 
 int m[MAX][MAX]; 
} Matrix; 
Matrix P = {1, 1,              //  p为     数列的    推导矩阵
           1, 0,
}; 
Matrix I = {1,0,                   //          I为 对应  P 的 单位矩阵
            0,1,
 }; 
 
Matrix matrixmul(Matrix a,Matrix b) //矩阵乘法
{ 
 int i,j,k; 
 Matrix c; 
 for (i = 0 ; i < MAX; i++) 
 for (j = 0; j < MAX;j++)
   { 
       c.m[i][j] = 0; 
      for (k = 0; k < MAX; k++) 
 c.m[i][j] += (a.m[i][k] * b.m[k][j])%mod; 
 c.m[i][j] %=mod；                //由于  当 n 太大时  ，  利用取模  可以求出  数列 的 后几位数    
 } 
 return c; 
} 
 
Matrix quickpow(long long n) 
{ 
 Matrix m = P, b = I; 
 while (n) 
 { 
     if (n & 1) 
          b = matrixmul(b,m); 
         n = n >> 1;   //    n=n/2；
         m = matrixmul(m,m); 
 } 
 return b; 
} 
使用：：：在：在在在 main()里直接调用 quickpow()就可以了。。。

2. 斐波那契数列 求前几位数 ，以 求前四位数 为例

在这里插入代码片 
      
123456.32=1234.56*10^2 
s=d.xxx*10^(len-4)             //  len 为  位数  =（int）log10（s）+1

log10(s)=log10(d.xxxxx)+log10(10^(len-4))=log10(d.xxxx)+len-4; 
log10(s)+4-len=log10(d.xxxx) 
d.xxxx=10^(log10(s)+4-len) 

s=(1/sqrt(5))*[(1+sqrt(5))/2.0]^n;      //  此处为   斐波那契数列  的数学公式 ， n 为 f【n】中的n

len=(int)log10(s)+1; 
d.xxxx=10^(log10(s)+4-((int)log10(s)+1))=10^(log10(s)-(int)log10(s)+3); 



核心代码：：：：        
           m =((1+sqrt(5))/2.0);
           k= (-0.5)*log10(5)+n*log10(m);          //k=log10(s);
          
           x=k-(int)k+3;

           ans=pow(10,x);
           printf("%lld\n",ans);              //   ans  必须用 整形 ，    .0lf 的double型 错

Fibonnacci Hdu3117

求前四位数 与后四位数

在这里插入代码片#include <iostream>
#include  <bits/stdc++.h>
using namespace std;
const int N=2;
typedef struct
{
    long long  m[N][N];
}matrix;//矩阵;

matrix P={0,1,
         1,1};       //  递推公式的 推导矩阵

matrix I={1,0,        //   单位矩阵
           0,1};

matrix   chengfa(matrix a,matrix b)
{
    int i,j,k;
    matrix c;
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
    {
        c.m[i][j]=0;
        for(int k=0;k<N;k++)
        {
            c.m[i][j]+=(a.m[i][k]*b.m[k][j]);
        }
        c.m[i][j]=c.m[i][j]%mod;                      // 若求  后4位数  则  mod=10000；

    }
    return c;
}
matrix quickpow(long long n)   // 矩阵快速幂，  p^n %mod   p 为推导矩阵
{
    matrix b=I,a=P;

    while(n)
    {
        if(n&1)
            b=chengfa(b,a);
        n=n/2;

        a=chengfa(a,a);
    }
    return b;

}


int main()
{  int f[100];
  long long ansqi,anshou,n;
  double k,a,x;
  matrix b;
  f[0]=0;
  f[1]=1;
  for(int i=2;i<=50;i++)
    f[i]=f[i-2]+f[i-1];

    /*for(int i=2;i<39;i++)
  printf("%d ",f[i]);*/


     while(cin>>n)
     {

         if(n>39)                   //由打表知道， 39 为 最后一个八位数；
        {

        a=(1+sqrt(5))/2.0;

        k=(-0.5)*log10(5)+n*log10(a);    //  k=log10(s);

        x=k-int(k)+3;

        ansqi=pow(10,x);



        b=quickpow(n);      // 所求为  f【n】的矩阵

        anshou=b.m[0][1]*f[1];

        printf("%lld...%04lld\n",ansqi,anshou);


        }
        else
            printf("%d\n",f[n]);


     }
    return 0;
}