[BZOJ 3811]玛里苟斯(线性基)尽量理解的题解

title

魔法之龙玛里苟斯最近在为加基森拍卖师的削弱而感到伤心，于是他想了一道数学题。
S 是一个可重集合，S={a1,a2,…,an}。
等概率随机取 S 的一个子集 A={ai1,…,aim}。
计算出 A 中所有元素异或和，记为 x, 求 x^k 的期望。

Input
第一行两个正整数 n, k。
以下 n 行每行一个整数，表示 ai。

Output
如果结果是整数，直接输出。如果结果是小数（显然这个小数是有限的），输出精确值（末尾不加多余的 0）。

Sample Input
4 2 0 1 2 3
Sample Output
3.5

Hint
限制与约定
1≤n≤100000，1≤k≤5，ai≥0。最终答案小于 2^63 。k=1,2,3,4,5 各自占用 20% 的数据

solution

期望=概率*答案值（我一直是这么计算期望这一类题目的）

直接走正解，废话不多说，因为我也不会引入
考虑 $k=1$的情况
我们把答案值 $ans$分解成二进制
如果第 $i$位上为 $1$，那么这个 $i$就会对答案造成 $1<<i$，即 $2^i$的贡献

那么我们怎么如何确定第 $i$位是不是 $1$呢？
很简单，看 $a$数组里面有多少个数二进制第 $i$位为 $1$
假设有 $x$个，可以知道在这 $x$个里面选择的个数的奇偶性会影响最后 $i$位是否为 $1$
选择了奇数个，异或后就是 $1$，否则就是 $0$
而剩下的 $n-x$个数不管选不选，都不会对 $i$这一位造成影响，因为这一位上面它们都是 $0$

那么在 $x$里面选择个数的奇偶性的概率又分别是多少呢？这里给出一个结论

奇偶性的概率一样，都是 $\frac{1}{2}$

我尽力感性证明一下
举个栗子 $2,6,10$，二进制分别为 $0010,0110,1010$
就只看从右往左数的第二位（ $i=1,2^i$），都是 $1$对吧。【注意从左往右第一位开始分别是 $2^0,2^1...$】
接着分类讨论
如果只选 $0$个，有 $1$种情况
如果只选 $1$个，有 $3$种情况
如果只选 $2$个，有 $3$种情况
如果只选 $3$个，有 $1$种情况

选偶数个的情况总数 $=>$选 $0$个 $+$选 $2$个： $1+3=4$
选奇数个的情况总数 $=>$选 $1$个 $+$选 $3$个： $1+3=4$
惊奇的一样！！

别急，再煮个栗子 $12，20，22，13$，二进制分别是 $01100,10100,10110,01101$，这一次就只看从左往右数的第三位( $i=2,2^i$)
如果只选 $0$个，有 $1$种情况
如果只选 $1$个，有 $4$种情况
如果只选 $2$个，有 $6$种情况
如果只选 $3$个，有 $4$种情况
如果只选 $4$个，有 $1$种情况
选偶数个的情况总数 $=>$选 $0$个 $+$选 $2$个 $+$选 $4$个： $1+6+1=8$
选奇数个的情况总数 $=>$选 $1$个 $+$选 $3$个： $4+4=8$
惊奇的又一样！！

而且仔细看这堆数字可以自然地联想到杨辉三角！！（其实是因为上面的情况可以看成组合数）

如果还是觉得很巧，不太有说服性，或者没想通的，我们再另辟蹊径
把这种奇偶选择操作看成按灯泡开关，上图！
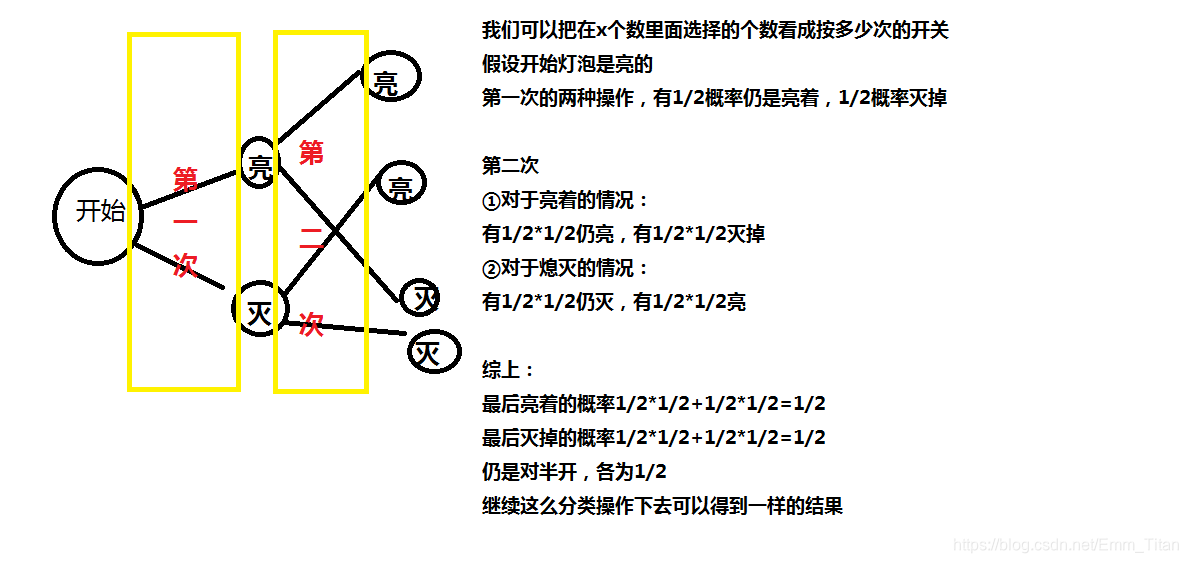
已经尽力了总结一下，只要有数能负责 $i$位，就会有一半的概率产生 $1<<i$的贡献

---

$k=2$的情况，最高位肯定小于 $33$， $i<33$
设 $f[s][i]$表示当选取情况为 $s$的时候， $i$这一位是 $1/0$，贡献就是 $f[s][i]^2=\sum_if[s][i]*\sum_jf[s][j]=\sum_i\sum_jf[s][i]*f[s][j]$
只有 $i=1,j=1$才会产生上面的贡献，即为 $1<<(i+j)=2^{i+j}$
接着我们来分类讨论，注意i，j表示二进制下的第i位，第j位为1/0
①： $i=0||j=0$
意思就是 $i,j$至少有一个是没有任何数可以负责的，就是没有任何一个数的二进制在那一位上面为 $1$
贡献自然是 $0$
②： $i=1\&\&j=1$
结合 $k=1$的情况下，我们知道选完数后要保证 $i$这一位上的值为 $1$才能对答案产生影响嘛
这个概率是 $\frac{1}{2}$， $j$同理，那么要让 $i,j$同时为 $1$，概率就是 $\frac{1}{2}*\frac{1}{2}=\frac{1}{4}$

但，BUT，However，unfortunately，unluckily

情况不止步于此，我们忽略掉了可能存在一些数二进制 $i,j$位都为 $1$
这样的话如果选择它，就会同步影响 $i,j$，所以我们要重新再分类讨论

结合 $k=1$按灯泡开关的思想，直接上图

---

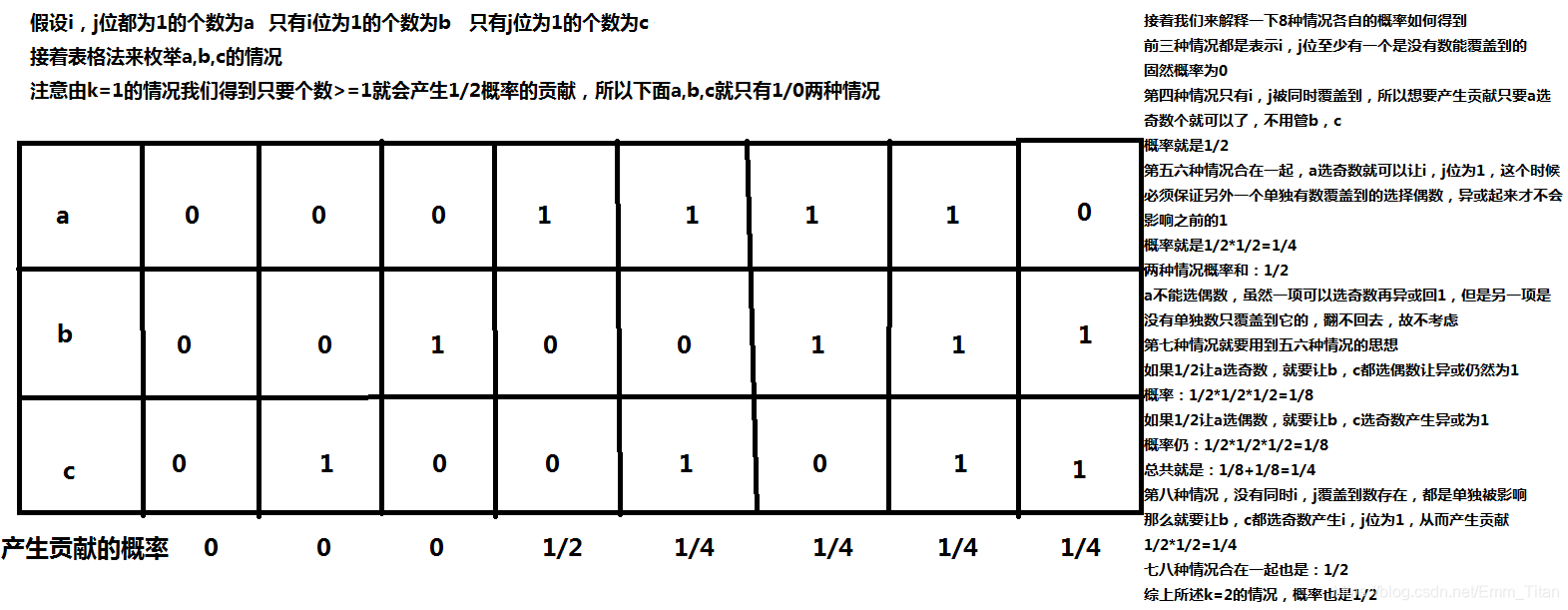
其实 $k>=3$的情况是最简单的，氧化钙！！
因为答案保证 $<2^{63}$，考虑第 $i$位会产生贡献，那么它对答案的影响就是 $(2^i)^k$，除掉 $k$
可以得到 $i<22$，比 $i$位更大的位置上一定都是 $0$
很容易想嘛，假设 $i=22$这位有 $1$就会产生 $(1<<22)^k$，最小的 $k=3$也会炸掉 $2^{63}$答案范围
所以我们就直接暴力枚举每一个数选与不选，生成子集 $A$，然后去算期望
注意只考虑线性基里面的每一个数，因为线性基可以异或出原数组的每一个数，自然也可以异或出原数组的异或和
记线性基的个数为 $m$
一共有 $2^m$种情况，每一种情况都是 $\frac{1}{2^m}$
用 $mod=1<<m$将期望拆开算，不然会炸 $unsigned\ long\ long$

code

#include <cstdio>
#define int unsigned long long
#define MAXN 100005
int n, k, ans, cnt, r;
int a[MAXN], f[65], s[65];
bool vis[65];

int read() {
	int x = 0; char s = getchar();
	while( s < '0' || s > '9' ) s = getchar();
	while( '0' <= s && s <= '9' )
		x = ( x << 1 ) + ( x << 3 ) + ( s - '0' ), s = getchar();
	return x;
}

void solve1() { 
	for( int i = 1;i <= n;i ++ ) ans |= a[i];
	if( ans & 1 ) printf( "%llu.5", ans >> 1 );
	else printf( "%llu", ans >> 1 );
}

bool check( int i, int j ) {
	if( ! vis[i] || ! vis[j] ) return 0;
	for( int t = 1;t <= n;t ++ ) {
		if( ( a[t] & ( 1ll << i ) ) && ! ( a[t] & ( 1ll << j ) ) )
			return 0;
		if( ( a[t] & ( 1ll << j ) ) && ! ( a[t] & ( 1ll << i ) ) )
			return 0;
	}
	return 1;
}

void solve2() {
	for( int i = 0;i < 33;i ++ )
		for( int j = 1;j <= n;j ++ )
			if( a[j] & ( 1ll << i ) ) { vis[i] = 1; break; }
	for( int i = 0;i < 33;i ++ )
		for(int j = i;j < 33;j ++ )
			if( vis[i] && vis[j] ) ans += ( 1ll << ( i + j ) );
	for( int i = 0;i < 33;i ++ )
		for( int j = i + 1;j < 33;j ++ )
			if( check( i, j ) ) ans += ( 1ll << ( i + j ) );
	if( ans & 1 ) printf( "%llu.5", ans >> 1 );
	else printf( "%llu", ans >> 1 );
}

void calc( int val ) {
	int mod = 1ll << cnt;
	int D = 0, R = 1;
	for( int i = 1;i <= k;i ++ )
		D = D * val, R = R * val, D += R / mod, R %= mod;
	ans += D, r += R, ans += r / mod, r %= mod;
}

void dfs( int x, int val ) {
	if( x > cnt ) { calc( val ); return; }
	dfs( x + 1, val ); dfs( x + 1, val ^ s[x] );
}

void solve3() {
	for( int i = 1;i <= n;i ++ ) {
		int val = a[i];
		for( int j = 21;~ j;j -- )
			if( ( 1ll << j ) & val )
				if( f[j] ) val ^= f[j];
				else { f[j] = val; break; }
	}
	for( int i = 0;i <= 21;i ++ )
		if( f[i] ) s[++ cnt] = f[i];
	dfs( 1, 0 );
	if( r ) printf( "%llu.5", ans );
	else printf( "%llu", ans );
}

signed main() {
	n = read(); k = read();
	for( int i = 1;i <= n;i ++ )
		a[i] = read();
	if( k == 1 ) solve1();
	else if( k == 2 ) solve2();
		else solve3();
	return 0;
}