RSA算法—— CTF 新手入门 (看完就能做题)
本文为个人学习笔记,仅供学习使用,由于本人基础知识薄弱,欢迎各位大佬批评指正!!!
就像小时候刚学各种方程一样,一上来就很吓唬人,觉得晦涩难懂,懂了就觉得很简单,有个循序渐进,由浅入深的过程。
为什么,为什么 要先放高级表达符号,搞的那么难懂呢???
想学的都是没学过的好奇小朋友!!
Let’s 先感性认识,再讲具体过程!
自己总结的小笔记 O(∩_∩)O
大佬别喷我…

一、初步认识


 懂又不懂
懂又不懂

二、简单理解
1. 百度解释
 迷迷糊糊,懵懵懂懂,马马虎虎
迷迷糊糊,懵懵懂懂,马马虎虎


大白话,通俗描述:
(1)选择一对不同的、足够大的素数p,q。
(2)计算n=pq。
(3)计算f(n)=(p-1)(q-1),同时对p, q严加保密,不让任何人知道。
(4)找一个与f(n)互质的数e,且1<e<f(n)。
(5)计算d,使得de≡1 mod f(n)。
这个公式也可以表达为
原文这个是错的!!! d ≡e-1 mod f(n) 应该是把e除到分母了
d ≡ e-1 mod f(n)
这里要解释一下,≡是数论中表示同余的符号。公式中,≡符号的左边必须和符号右边同余,也就是两边模运算结果相同。显而易见,不管f(n)取什么值,符号右边1 mod f(n)的结果都等于1;符号的左边d与e的乘积做模运算后的结果也必须等于1。这就需要计算出d的值,让这个同余等式能够成立。
(6)公钥KU=(e,n),私钥KR=(d,n)。
(7)加密时,先将明文变换成0至n-1的一个整数M。若明文较长,可先分割成适当的组,然后再进行交换。
Gamma(z) = \int_0^\infty t{z-1}e{-t}dt,.
$$
2.带你彻底理解RSA算法原理
(1)加密:


RSA加密是对明文的E次方后除以N后求余数的过程。
只要知道E和N任何人都可以进行RSA加密了,所以说E、N是RSA加密的密钥,也就是说E和N的组合就是公钥,用(E,N)来表示公钥。
(E、N有特别要求,暂时不管)
E:Encryption 加密
N:Number 数字
(2) 解密

RSA解密,密文进行D次方后除以N的余数就是明文。

知道D和N就能进行解密密文了,所以D和N的组合就是私钥
RSA的加密方式和解密方式是相同的
加密是求 E次方的mod N
解密是求 D次方的mod N
D:Decryption 解密
N:Number 数字

后面作者说的很详细了



学的差不多了?来深入了解一下!
三、深入理解
就讲的很好!
1.阮一峰——RSA算法原理(一)
2.阮一峰——RSA算法原理(二)
四、附必要的数学基础:
-
基础整合
黄映焜的博客园 ( 基础知识整合 ) -
公式图表

-
质数(素数):
一个大于1的自然数,除了1和它本身外,不能被其他自然数整除(除0以外)的数称之为质数(素数);否则称为合数。 -
互质数:公约数只有1的两个数,叫做互质数。
判别方法主要有以下几种(不限于此):
(1)两个质数一定是互质数。例如,2与7、13与19。
(2)一个质数如果不能整除另一个合数,这两个数为互质数。例如,3与10、5与 26。
(3)1不是质数也不是合数,它和任何一个自然数在一起都是互质数。如1和9908。
(4)相邻的两个自然数是互质数。如 15与 16。
(5)相邻的两个奇数是互质数。如 49与 51。
(6)大数是质数的两个数是互质数。如97与88。
(7)小数是质数,大数不是小数的倍数的两个数是互质数。如 7和 16。
(8)两个数都是合数(二数差又较大),小数所有的质因数,都不是大数的约数,这两个数是互质数。如357与715,357=3×7×17,而3、7和17都不是715的约数,这两个数为互质数。等等。
- 模运算:模运算是整数运算,有一个整数m,以n为模做模运算,即m mod n。用m去被n整除,只取所得的余数作为结果,就叫做模运算。例如,10 mod 3=1;26 mod 6=2;28 mod 2 =0。
a ≡ b (mod n)
原文表述错误: 给定一个正整数m,如果两个整数a和b满足a-b能被m整除,即(a-b)modm=0, 那么就称整数a与b对模m同余,记作a≡b(modm),同时可成立amodm=b ,再次提醒注意,同余与模运算是不同的
查了百度,不是非要0,而且不能那么说吧。
数论中的重要概念。给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。
≡ 表示同余,即MOD的符号,表示模。
a和b除以n后余数相同,读作a与b同余,mod为n。
如果我们以3为模,则4与7就是关于3同余的。记作7≡4 (mod 3),8≡5 (mod 3),26≡5 (mod 7)。
简单理解,当取余,python立面自己试试看,1%20=1,千万不要当作是20
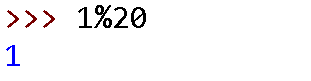
同余涉及:欧拉定理,费马小定理,中国剩余定理(孙子定理)
假设用户A需要将明文“key”通过RSA加密后传递给用户B,过程如下:
(1)设计公私密钥(e,n)和(d,n)。
令p=3,q=11,得出n=p×q=3×11=33;f(n)=(p-1)(q-1)=2×10=20;取e=3,(3与20互质)则e×d≡1 mod f(n),即3×d≡1 mod 20。
d怎样取值呢?可以用试算的办法来寻找。
试算结果见下表:

当d=7时,3x7 mod 20 = 1 mod 20 = 1,即 e×d≡1 mod f(n)同余等式成立。因此,可令d=7。从而我们可以设计出一对公私密钥,加密密钥(公钥)为:KU =(e,n)=(3,33),解密密钥(私钥)为:KR =(d,n)=(7,33)。
(2)英文数字化。
将明文信息数字化,并将每块两个数字分组。假定明文英文字母编码表为按字母顺序排列数值,即:

则得到分组后的key的明文信息为:11,05,25。
(3)明文加密
用户加密密钥(3,33) 将数字化明文分组信息加密成密文。由C≡Me(mod n)得:
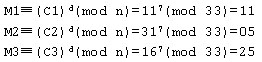
因此,得到相应的密文信息为:11,31,16。
 6. 欧拉函数
6. 欧拉函数
任意给定正整数n,计算在小于等于n的正整数之中,有多少个与n构成互质关系?
计算这个值的方法就叫做欧拉函数,以φ(n)表示.
例如,在1到8之中,与8形成互质关系的是1、3、5、7,所以φ(n)=4
在RSA算法中,我们需要明白欧拉函数对以下定理成立
如果n可以分解成两个互质的整数之积,即n=p×q,则有:φ(n)=φ(pq)=φ(p)φ(q);
根据“大数是质数的两个数一定是互质数”可以知道:
一个数如果是质数,则小于它的所有正整数与它都是互质数;
所以如果一个数p是质数,则有:φ(p)=p-1
由上易得,若我们知道一个数n可以分解为两个质数p和q的乘积,则有
φ(n)=(p-1)(q-1)
五、CTF例题
一起来做做你曾经望而生畏的简单题
- Bugku
 rsa.txt
rsa.txt
https://ctf.bugku.com/files/98e8f374f63ee3ef4818621ceafcb78f/rsa.txt
N : 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597
e : 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619
enc : 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
给了n,e,c(c就是密文,就是给的enc,你可能会猜这是什么变量,encode加密编码,decode解密解码),求明文m

对着之前的图想想,n分离出 p、q
可以用Wiener’s attack脚本分解质数
def continued_fractions_expansion(numerator,denominator):#(e,N)
result=[]
divident=numerator%denominator
quotient=numerator/denominator
result.append(quotient)
while divident!=0:
numerator=numerator-quotient*denominator
tmp=denominator
denominator=numerator
numerator=tmp
divident=numerator%denominator
quotient=numerator/denominator
result.append(quotient)
return result
def convergents(expansion):
convergents=[(expansion[0],1)]
for i in range(1,len(expansion)):
numerator=1
denominator=expansion[i]
for j in range(i-1,-1,-1):
numerator+=expansion[j]*denominator
if j==0:
break
tmp=denominator
denominator=numerator
numerator=tmp
convergents.append((numerator,denominator))#(k,d)
return convergents
def newtonSqrt(n):
approx = n/2
better = (approx + n/approx)/2
while better != approx:
approx = better
better = (approx + n/approx)/2
return approx
def wiener_attack(cons,e,N):
for cs in cons:
k,d=cs
if k==0:
continue
phi_N=(e*d-1)/k
#x**2-((N-phi_N)+1)*x+N=0
a=1
b=-((N-phi_N)+1)
c=N
delta = b*b - 4*a*c
if delta<=0:
continue
x1= (newtonSqrt(delta)-b)/(2*a)
x2=-(newtonSqrt(delta)+b)/(2*a)
if x1*x2==N:
return [x1,x2,k,d]
N=460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597
e=354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619
expansion=continued_fractions_expansion(e,N)
cons=convergents(expansion)
p,q,k,d=wiener_attack(cons,e,N)
print 'p\n', p
print 'q\n', q
p
28805791771260259486856902729020438686670354441296247148207862836064657849735343618207098163901787287368569768472521344635567334299356760080507454640207003
q
15991846970993213322072626901560749932686325766403404864023341810735319249066370916090640926219079368845510444031400322229147771682961132420481897362843199
求出了p、q,那就能求出来 (p-1)(q-1) = ∮
已知了n、e、c、p、q、∮、求m
import binascii
import sys
sys.setrecursionlimit(1000000)
def ByteToHex(bins):
return ''.join(["%02X" % x for x in bins]).strip()
def n2s(num):
t = hex(num)[2:-1] # python
if len(t) % 2 == 1:
t = '0' + t
#print(t)
return(binascii.a2b_hex(t).decode('latin1'))
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
print('modular inverse does not exist')
return 'null'
else:
return x % m
c = 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
p = 28805791771260259486856902729020438686670354441296247148207862836064657849735343618207098163901787287368569768472521344635567334299356760080507454640207003
q = 15991846970993213322072626901560749932686325766403404864023341810735319249066370916090640926219079368845510444031400322229147771682961132420481897362843199
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619
n = p * q
d = modinv(e, (p - 1) * (q - 1))
m = pow(c, d, n)
print 'm \n', m
flag{Wien3r_4tt@ck_1s_3AsY}
本文为个人学习笔记,仅供学习使用,由于本人基础知识薄弱,欢迎各位大佬批评指正!!!
