BP训练多层感知器摘记

1. 多层感知器

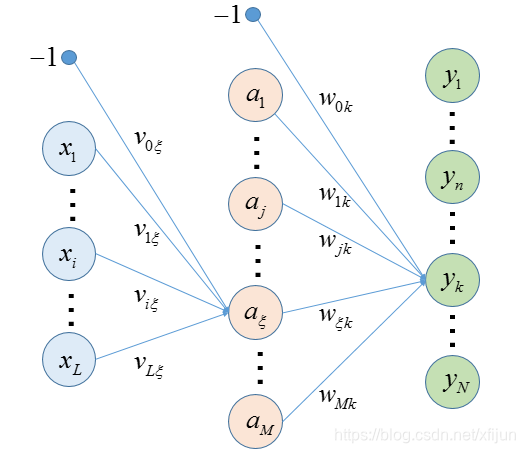
$\qquad$本文只考虑一个隐层的情况。

• 输入层有 $L$个单元（不包含偏置， $x_{i}$ 为第 $i$ 个输入单元），隐层有 $M$个单元（不包含偏置， $a_{j}$ 为第 $j$ 个隐层单元），输出层有 $N$个单元（ $y_{k}$ 为第 $k$ 个输出单元）。
• 输入层的权值为 $\boldsymbol{v}=[v_{i\xi}]$，隐层的权值为 $\boldsymbol{w}=[w_{jk}]$
  $\newline\qquad$ $\newline$

$\qquad$对于第 $\xi$ 个隐层单元 $a_{\xi}$，假设激活函数为 $g(\cdot)$，通常为 $sigmoid$ 函数，则：
$\newline$
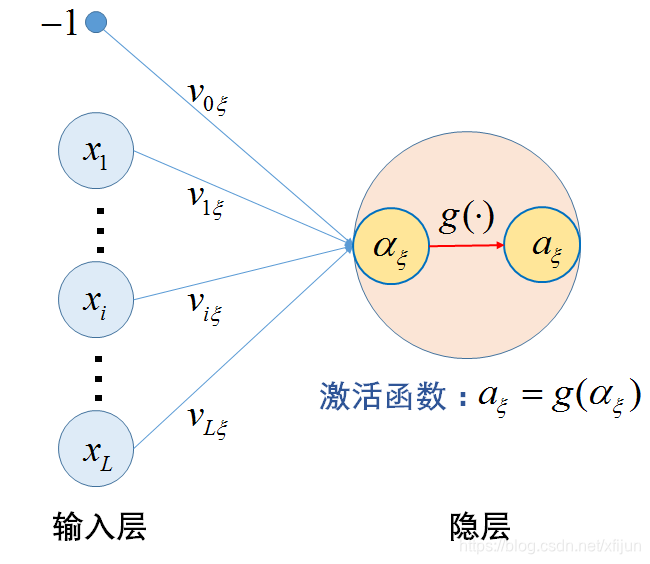
$\qquad \qquad a_{\xi}=g(\alpha_{\xi})=g\left(\displaystyle\sum_{i=0}^{L}x_{i}v_{i\xi}\right) \ \qquad\qquad\qquad\qquad\qquad(1)\newline$
$\qquad\qquad$其中， $x_{0}=-1$
$\newline\qquad\qquad$

隐层单元的激活函数 $g(\cdot)$

$\qquad$对于第 $k$ 个输出单元 $y_{k}$，假设激活函数为 $h(\cdot)$，则：
$\newline$
$\qquad \qquad y_{k}=h(\beta_{k})=h\left(\displaystyle\sum_{j=0}^{M}a_{j}w_{jk}\right) \qquad\qquad\qquad\qquad\qquad(2)$

$\qquad\qquad$其中， $a_{0}=-1$

$\newline\qquad\qquad$

输出层单元的激活函数 $h(\cdot)$

• 对于回归问题， $h(\cdot)$为 $“$恒等函数 $”$，即 $h(\beta_{k})=\beta_{k}$
• 对于分类问题， $h(\cdot)$为 $“$softmax函数 $”$，即 $h(\beta_{k})=\dfrac{e^{\beta_{k}}}{\sum\limits_{n=1}^{N}e^{\beta_{n}}}=\dfrac{e^{\beta_{k}}}{ e^{\beta_{1}}+\cdots+e^{\beta_{k}}+\cdots+e^{\beta_{N}}}$

2. 前向传播过程

$\boldsymbol{2.1}\ \ \ 前向传播过程示意图\newline$
$\qquad$感知器 $(perceptron)$只能解决线性分类问题，通过感知器的 $“$叠加层 $”$，可以形成多层感知器 $(multilayer\ perceptron)$，可以进行更复杂的表示。

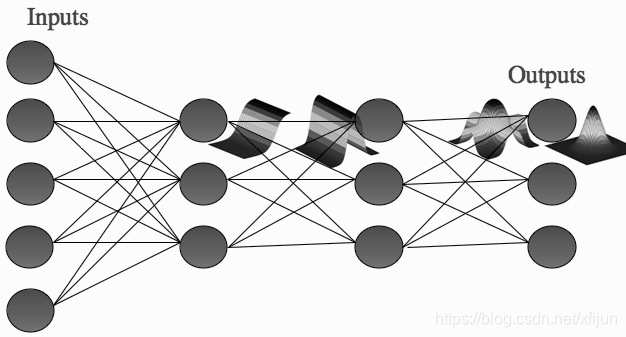
引自Machine Learning - An Algorithmic Perspective 2nd Edition，Fig 4.9
图(a)大致可认为是一个sigmoid神经元所形成的"分类面"，图(b) ~ (d)为不同的sigmoid神经元的叠加所形成的"分类面"

引自Machine Learning - An Algorithmic Perspective 2nd Edition，Fig 4.10
多层感知器学习过程示意图

• 多层感知器的所有参数为 $(\boldsymbol{v}, \boldsymbol{w})$
• 若经过训练的多层感知器的参数为 $(\boldsymbol{v}, \boldsymbol{w})$，对于某个输入 $\boldsymbol{x}$，其输出值为函数 $y_{k}(\boldsymbol{x},\boldsymbol{v}, \boldsymbol{w})$

$\qquad y_{k}(\boldsymbol{x},\boldsymbol{v}, \boldsymbol{w})=h \left( \displaystyle\sum_{j=0}^{M}w_{jk}g\left( \displaystyle\sum_{i=0}^{L}v_{ij}x_{i}\right) \right)\ ,\ k=1,\cdot\cdot\cdot,N\qquad(3)$

$\boldsymbol{2.2}\ \ \ sequential\ 和\ batch\ 两种训练模式时的数据表示$

• $sequential$ 对应单个输入的情况，即顺序模式 $\newline$
  $\qquad$假设单个训练数据为 $\{\boldsymbol{x},\boldsymbol{t}\}$
  $\qquad$ $\boldsymbol{x} \in R^{L+1}$ 为输入数据，即 $\boldsymbol{x}=(x_{0},x_{1},\cdot\cdot\cdot,x_{L})$，其中 $x_{0}=-1$
  $\qquad$ $\boldsymbol{t} \in R^{N}$为期望输出，即 $\boldsymbol{t}=(t_{1},t_{2},\cdot\cdot\cdot,t_{N})$
  $\qquad$通过多层感知器之后的输出为 $\boldsymbol{y} \in R^{N}$，即 $\boldsymbol{y}=(y_{1},y_{2},\cdot\cdot\cdot,y_{N})$
  $\qquad$训练该数据所产生的误差定义为： $E=\dfrac{1}{2}\displaystyle\sum_{k=1}^{N}(y_{k}-t_{k})^{2}$
  $\newline$
• $batch$ 对应多个输入数据的情况，即批处理模式 $\newline$
  $\qquad$假设 $P$ 个训练数据为 $\{\boldsymbol{x}^{(p)},\boldsymbol{t}^{(p)}\}_{p=1}^{P}$
  $\qquad$ $\boldsymbol{x}^{(p)} \in R^{L+1}$ 为输入数据，即 $\boldsymbol{x}^{(p)}=(x_{0}^{(p)},x_{1}^{(p)},\cdot\cdot\cdot,x_{L}^{(p)})$，其中 $x_{0}^{(p)}=-1$
  $\qquad$ $\boldsymbol{t}^{(p)} \in R^{N}$ 为期望输出，即 $\boldsymbol{t}^{(p)}=(t_{1}^{(p)},t_{2}^{(p)},\cdot\cdot\cdot,t_{N}^{(p)})$
  $\qquad$通过多层感知器之后的输出为 $\boldsymbol{y}^{(p)} \in R^{N}$，即 $\boldsymbol{y}^{(p)}=(y_{1}^{(p)},y_{2}^{(p)},\cdot\cdot\cdot,y_{N}^{(p)})$
  $\qquad$训练这一批数据所产生的平均误差定义为： $E=\dfrac{1}{2P}\displaystyle\sum_{p=1}^{P}\left( \displaystyle\sum_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)})^{2}\right)$
  $\newline$

$\boldsymbol{2.3}\ \ \ 相关矩阵表示$

• $3个数据矩阵：$
  $1)$ 输入矩阵，第 $p$行表示第 $p$个输入数据 $\boldsymbol{x}^{(p)}$，最后一列的 $“-1”$ 表示偏置 $\newline$
  $\qquad inputs:\qquad\left[ \begin{matrix} x_{1}^{(1)} & \cdots & x_{i}^{(1)} & \cdots & x_{L}^{(1)} & -1 \\ \vdots & & \vdots & & \vdots & \vdots \\ x_{1}^{(p)} & \cdots & x_{i}^{(p)} & \cdots & x_{L}^{(p)} & -1 \\ \vdots & & \vdots& & \vdots & \vdots \\ x_{1}^{(P)} & \cdots & x_{i}^{(P)} & \cdots & x_{L}^{(P)} & -1 \end{matrix} \right]_{P\times (L+1)} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \newline$

$\qquad2)$ 隐层矩阵，第 $p$行表示第 $p$个输入 $\boldsymbol{x}^{(p)}$所对应的隐层节点数据 $\boldsymbol{a}^{(p)}$，最后一列的 $“-1”$ 表示偏置 $\newline$
$\qquad \qquad hidden:\qquad\left[ \begin{matrix} a_{1}^{(1)} & \cdots & a_{j}^{(1)} & \cdots & a_{M}^{(1)} & -1 \\ \vdots & & \vdots & & \vdots & \vdots \\ a_{1}^{(p)} & \cdots & a_{j}^{(p)} & \cdots & a_{M}^{(p)} & -1 \\ \vdots & & \vdots& & \vdots & \vdots \\ a_{1}^{(P)} & \cdots & a_{j}^{(P)} & \cdots & a_{M}^{(P)} & -1 \end{matrix} \right]_{P\times (M+1)} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \newline$
$\qquad\qquad$[注]：两个矩阵的偏置 $-1$ 放在最后一列是为了便于编程实现，后续都采用该方式描述 $\boldsymbol{x}^{(p)}$ 和 $\boldsymbol{a}^{(p)}$ $\newline$
$\qquad 3)$ 输出矩阵，第 $p$行表示第 $p$个输入 $\boldsymbol{x}^{(p)}$所对应的输出值 $\boldsymbol{y}^{(p)} \newline$
$\qquad \qquad output:\qquad\left[ \begin{matrix} y_{1}^{(1)} & \cdots & y_{k}^{(1)} & \cdots & y_{N}^{(1)} \\ \vdots & & \vdots & & \vdots \\ y_{1}^{(p)} & \cdots & y_{k}^{(p)} & \cdots & y_{N}^{(p)} \\ \vdots & & \vdots& & \vdots \\ y_{1}^{(P)} & \cdots & y_{k}^{(P)} & \cdots & y_{N}^{(P)} \end{matrix} \right]_{P \times N} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \newline$

$\qquad 4)$ 目标值矩阵，第 $p$行表示第 $p$个输入 $\boldsymbol{x}^{(p)}$所对应的目标值 $\boldsymbol{t}^{(p)} \newline$
$\qquad \qquad target:\qquad\left[ \begin{matrix} t_{1}^{(1)} & \cdots & t_{k}^{(1)} & \cdots & t_{N}^{(1)} \\ \vdots & & \vdots & & \vdots \\ t_{1}^{(p)} & \cdots & t_{k}^{(p)} & \cdots & t_{N}^{(p)} \\ \vdots & & \vdots& & \vdots \\ t_{1}^{(P)} & \cdots & t_{k}^{(P)} & \cdots & t_{N}^{(P)} \end{matrix} \right]_{P \times N} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \newline$

• $2个系数矩阵：$
  $1)$ 输入系数矩阵，第 $j$列 表示第 $j$ 个隐层节点对应于输入层节点的系数 $\newline$
  $\qquad weights1:\qquad\left[ \begin{matrix} v_{11} & \cdots & v_{1j} & \cdots & v_{1M} \\ \vdots & & \vdots & & \vdots \\ v_{i1} & \cdots & v_{ij} & \cdots & v_{iM} \\ \vdots & & \vdots& & \vdots \\ v_{L1} & \cdots & v_{Lj} & \cdots & v_{LM} \\ v_{01} & \cdots & v_{0j} & \cdots & v_{0M} \end{matrix} \right]_{(L+1) \times M}$
  $\qquad \qquad\qquad\qquad\qquad\qquad\qquad\ \ \uparrow \newline$

$\qquad 2)$ 隐层系数矩阵，第 $k$ 列表示第 $k$ 个输出节点对应于隐层节点的系数 $\newline$
$\qquad\qquad weights2:\qquad\left[ \begin{matrix} w_{11} & \cdots & w_{1k} & \cdots & w_{1N} \\ \vdots & & \vdots & & \vdots \\ w_{j1} & \cdots & w_{jk} & \cdots & w_{jN} \\ \vdots & & \vdots& & \vdots \\ w_{M1} & \cdots & w_{Mk} & \cdots & w_{MN} \\ w_{01} & \cdots & w_{0k} & \cdots & w_{0N} \end{matrix} \right]_{(M+1) \times N}$
$\qquad \qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \ \ \ \uparrow \newline$
$\boldsymbol{2.4}\ \ \ 前向传播过程的实现\newline$
$\qquad$定义了这些矩阵之后，前向传播过程的公式 $(3)$的计算过程可表示为： $\newline$
$\qquad$(1) 构造 $inputs_{P \times (L+1)}$ 矩阵，即在输入数据矩阵 $(P \times L$维 $)$的最后一列加上值为 $-1$的偏置 $\newline$

$\qquad$ $\qquad$输入数据矩阵 $:$

$\qquad$ $\begin{aligned} \qquad\qquad \left[ \begin{matrix} x_{1}^{(1)} & \cdots & x_{i}^{(1)} & \cdots & x_{L}^{(1)} \\ \vdots & & \vdots & & \vdots \\ x_{1}^{(p)} & \cdots & x_{i}^{(p)} & \cdots & x_{L}^{(p)} \\ \vdots & & \vdots& & \vdots \\ x_{1}^{(P)} & \cdots & x_{i}^{(P)} & \cdots & x_{L}^{(P)} \end{matrix} \right] _{P\times L} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \ 第p个输入的训练数据\boldsymbol{x}^{(p)} \end{aligned} \newline$

$\qquad$(2) 计算各个隐层节点的输入值 $\boldsymbol{\alpha}^{(p)}$，也就是 $input *weights1$ 矩阵 $(P \times M$维 $)$的第 $p$ 行 $\newline$

$\qquad$ $\begin{aligned} \qquad& inputs_{P\times (L+1)}*weights1_{(L+1) \times M} \\ &= \left[ \begin{matrix} x_{1}^{(1)} & \cdots & x_{i}^{(1)} & \cdots & x_{L}^{(1)} & -1 \\ \vdots & & \vdots & & \vdots & \vdots \\ x_{1}^{(p)} & \cdots & x_{i}^{(p)} & \cdots & x_{L}^{(p)} & -1 \\ \vdots & & \vdots& & \vdots & \vdots \\ x_{1}^{(P)} & \cdots & x_{i}^{(P)} & \cdots & x_{L}^{(P)} & -1 \end{matrix} \right] \left[ \begin{matrix} v_{11} & \cdots & v_{1j} & \cdots & v_{1M} \\ \vdots & & \vdots & & \vdots \\ v_{i1} & \cdots & v_{ij} & \cdots & v_{iM} \\ \vdots & & \vdots& & \vdots \\ v_{L1} & \cdots & v_{Lj} & \cdots & v_{LM} \\ v_{01} & \cdots & v_{0j} & \cdots & v_{0M} \end{matrix} \right] \\ &= \left[ \begin{matrix} \sum\limits_{i=0}^{L} x_{i}^{(1)}v_{i1} & \cdots & \sum\limits_{i=0}^{L} x_{i}^{(1)}v_{ij} & \cdots & \sum\limits_{i=0}^{L} x_{i}^{(1)}v_{iM} \\ \vdots & & \vdots & & \vdots \\ \sum\limits_{i=0}^{L} x_{i}^{(p)}v_{i1} & \cdots & \sum\limits_{i=0}^{L} x_{i}^{(p)}v_{ij} & \cdots & \sum\limits_{i=0}^{L} x_{i}^{(p)}v_{iM} \\ \vdots & & \vdots& & \vdots \\ \sum\limits_{i=0}^{L} x_{i}^{(P)}v_{i1} & \cdots & \sum\limits_{i=0}^{L} x_{i}^{(P)}v_{ij} & \cdots & \sum\limits_{i=0}^{L} x_{i}^{(P)}v_{iM} \end{matrix} \right] _{P\times M} \\ &= \left[ \begin{matrix} \alpha_{1}^{(1)} & \cdots & \alpha_{j}^{(1)} & \cdots & \alpha_{M}^{(1)} \\ \vdots & & \vdots & & \vdots \\ \alpha_{1}^{(p)} & \cdots & \alpha_{j}^{(p)} & \cdots & \alpha_{M}^{(p)} \\ \vdots & & \vdots& & \vdots \\ \alpha_{1}^{(P)} & \cdots & \alpha_{j}^{(P)} & \cdots & \alpha_{M}^{(P)} \end{matrix} \right] _{P\times M} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \ 第p个输入\boldsymbol{x}^{(p)}所对应隐层节点的输入 \end{aligned} \newline$

$\qquad$(3) 将隐层节点的输入值，通过 $sigmoid$ 激活函数 $g(\cdot)$，转变为隐层节点输出值 $\boldsymbol{a}^{(p)}=g(\boldsymbol{\alpha}^{(p)})$ $\newline$

$\qquad$ $\qquad$隐层节点输出值矩阵 $:g(inputs*weights1)$

$\qquad$ $\begin{aligned} \qquad& g(inputs*weights1) \\ &=g\left( \left[ \begin{matrix} \alpha_{1}^{(1)} & \cdots & \alpha_{j}^{(1)} & \cdots & \alpha_{M}^{(1)} \\ \vdots & & \vdots & & \vdots \\ \alpha_{1}^{(p)} & \cdots & \alpha_{j}^{(p)} & \cdots & \alpha_{M}^{(p)} \\ \vdots & & \vdots& & \vdots \\ \alpha_{1}^{(P)} & \cdots & \alpha_{j}^{(P)} & \cdots & \alpha_{M}^{(P)} \end{matrix} \right] _{P\times M}\right) \\ &=\left[ \begin{matrix} a_{1}^{(1)} & \cdots & a_{j}^{(1)} & \cdots & a_{M}^{(1)} \\ \vdots & & \vdots & & \vdots \\ a_{1}^{(p)} & \cdots & a_{j}^{(p)} & \cdots & a_{M}^{(p)} \\ \vdots & & \vdots& & \vdots \\ a_{1}^{(P)} & \cdots & a_{j}^{(P)} & \cdots & a_{M}^{(P)} \end{matrix} \right] _{P\times M} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \ 第p个输入\boldsymbol{x}^{(p)}所对应的隐层节点数据 \end{aligned} \newline$

$\qquad$(4) 构造 $hidden_{P \times (M+1)}$ 矩阵，即在隐层节点输出值矩阵 $(P \times M$维 $)$的最后一列加上值为 $-1$ 的偏置 $\newline$

$\qquad \qquad hidden:\left[ \begin{matrix} a_{1}^{(1)} & \cdots & a_{j}^{(1)} & \cdots & a_{M}^{(1)} & -1 \\ \vdots & & \vdots & & \vdots & \vdots \\ a_{1}^{(p)} & \cdots & a_{j}^{(p)} & \cdots & a_{M}^{(p)} & -1 \\ \vdots & & \vdots& & \vdots & \vdots \\ a_{1}^{(P)} & \cdots & a_{j}^{(P)} & \cdots & a_{M}^{(P)} & -1 \end{matrix} \right] \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \ 第p个输入\boldsymbol{x}^{(p)}所对应的隐层节点数据\boldsymbol{a}^{(p)}\newline$

$\qquad$(5) 计算各个输出节点的输入值 $\boldsymbol{\beta}^{(p)}$，也就是 $hidden *weights2$ 矩阵 $(P \times N$维 $)$的第 $p$ 行 $\newline$

$\qquad$ $\begin{aligned} \qquad& hidden_{P\times (M+1)}*weights2_{(M+1) \times N} \\ &= \left[ \begin{matrix} a_{1}^{(1)} & \cdots & a_{j}^{(1)} & \cdots & a_{M}^{(1)} & -1 \\ \vdots & & \vdots & & \vdots & \vdots \\ a_{1}^{(p)} & \cdots & a_{j}^{(p)} & \cdots & a_{M}^{(p)} & -1 \\ \vdots & & \vdots& & \vdots & \vdots \\ a_{1}^{(P)} & \cdots & a_{j}^{(P)} & \cdots & a_{M}^{(P)} & -1 \end{matrix} \right] \left[ \begin{matrix} w_{11} & \cdots & w_{1k} & \cdots & w_{1N} \\ \vdots & & \vdots & & \vdots \\ w_{j1} & \cdots & w_{jk} & \cdots & w_{jN} \\ \vdots & & \vdots& & \vdots \\ w_{M1} & \cdots & w_{Mk} & \cdots & w_{MN} \\ w_{01} & \cdots & w_{0k} & \cdots & w_{0N} \end{matrix} \right] \\ &= \left[ \begin{matrix} \sum\limits_{j=0}^{M} a_{j}^{(1)}w_{j1} & \cdots & \sum\limits_{j=0}^{M} a_{j}^{(1)}w_{jk} & \cdots & \sum\limits_{j=0}^{M} a_{j}^{(1)}w_{jN} \\ \vdots & & \vdots & & \vdots \\ \sum\limits_{j=0}^{M} a_{j}^{(p)}w_{j1} & \cdots & \sum\limits_{j=0}^{M} a_{j}^{(p)}w_{jk} & \cdots & \sum\limits_{j=0}^{M} a_{j}^{(p)}w_{jN} \\ \vdots & & \vdots& & \vdots \\ \sum\limits_{j=0}^{M} a_{j}^{(P)}w_{j1} & \cdots & \sum\limits_{j=0}^{M} a_{j}^{(P)}w_{jk} & \cdots & \sum\limits_{j=0}^{M} a_{j}^{(P)}w_{jN} \end{matrix} \right] _{P\times N} \\ &= \left[ \begin{matrix} \beta_{1}^{(1)} & \cdots & \beta_{k}^{(1)} & \cdots & \beta_{N}^{(1)} \\ \vdots & & \vdots & & \vdots \\ \beta_{1}^{(p)} & \cdots & \beta_{k}^{(p)} & \cdots & \beta_{N}^{(p)} \\ \vdots & & \vdots& & \vdots \\ \beta_{1}^{(P)} & \cdots & \beta_{k}^{(P)} & \cdots & \beta_{N}^{(P)} \end{matrix} \right] _{P\times N} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \ 第p个输入\boldsymbol{x}^{(p)}所对应输出节点的输入 \end{aligned} \newline$

$\qquad$(6) 将输出节点的输入值，通过激活函数 $h(\cdot)$，转变为输出层节点的输出值 $\boldsymbol{y}^{(p)}=h(\boldsymbol{\beta}^{(p)})\newline$

$\qquad$ $\qquad$输出层节点的输出值矩阵 $:h(hidden*weights2)$

$\qquad$ $\begin{aligned} \qquad& h(hidden*weights2) \\ &=h \left( \left[ \begin{matrix} \beta_{1}^{(1)} & \cdots & \beta_{k}^{(1)} & \cdots & \beta_{N}^{(1)} \\ \vdots & & \vdots & & \vdots \\ \beta_{1}^{(p)} & \cdots & \beta_{k}^{(p)} & \cdots & \beta_{N}^{(p)} \\ \vdots & & \vdots& & \vdots \\ \beta_{1}^{(P)} & \cdots & \beta_{k}^{(P)} & \cdots & \beta_{N}^{(P)} \end{matrix} \right] _{P\times N} \right) \\ &= \left[ \begin{matrix} y_{1}^{(1)} & \cdots & y_{k}^{(1)} & \cdots & y_{N}^{(1)} \\ \vdots & & \vdots & & \vdots \\ y_{1}^{(p)} & \cdots & y_{k}^{(p)} & \cdots & y_{N}^{(p)} \\ \vdots & & \vdots& & \vdots \\ y_{1}^{(P)} & \cdots & y_{k}^{(P)} & \cdots & y_{N}^{(P)} \end{matrix} \right] _{P\times N} \begin{matrix} \\ \\ \longleftarrow\\ \\ \\ \end{matrix} \ 第p个输入\boldsymbol{x}^{(p)}所对应的输出节点数据 \end{aligned} \newline$

$\qquad$当 $h(\cdot)$为恒等函数时，前向传播过程用python可以描述为：

inputs = np.concatenate((inputs,-np.ones((self.ndata,1))),axis=1) #构造input矩阵, Px(L+1)维
hidden = np.dot(inputs,weights1)              # inputs*weights1的结果为 PxM维                               
hidden = 1.0/(1.0+np.exp(-hidden))            # sigmoid激活函数
hidden = np.concatenate((hidden,-np.ones((np.shape(inputs)[0],1))),axis=1)  #构造hidden矩阵, Px(M+1)维
output = np.dot(hidden,weights2)                                  #产生output矩阵, PxN维

3. 误差反向传递

$\qquad$权值的训练采用误差修正学习，通过误差在多层感知器中的反向传递，通过调整各层的权值来减小训练误差，权重的调整主要使用梯度下降法（ $\eta$为学习率）： $\newline$
$\qquad$隐层权值： 　 $w_{jk}=w_{jk} + \Delta w_{jk} = w_{jk}-\eta \dfrac{\partial E}{\partial w_{jk}} \qquad\qquad\qquad(4)\newline$
$\qquad$输入层权值： $v_{ij}=v_{ij} + \Delta v_{ij} =v_{ij}-\eta \dfrac{\partial E}{\partial v_{ij}} \qquad\qquad\qquad\qquad(5)$

$\boldsymbol{3.1}\ \ \ sequential\ 模式\newline$
$\qquad$每次进入单个训练数据，前向传播得到输出值之后，再通过误差反向传递来训练所有权值 $\left(\boldsymbol{v},\boldsymbol{w}\right)$。
$\qquad$假设单个训练数据为 $\{\boldsymbol{x},\boldsymbol{t}\}$，即输入 $\boldsymbol{x}=(x_{1},\cdot\cdot\cdot,x_{L},-1)$，对应目标值 $\boldsymbol{t}=(t_{1},t_{2},\cdot\cdot\cdot,t_{N})$，通过多层感知器后的输出值为 $\boldsymbol{y}=(y_{1},y_{2},\cdot\cdot\cdot,y_{N})$
$\qquad$训练该数据所产生的误差为：
$\qquad\qquad E=\dfrac{1}{2}\displaystyle\sum_{k=1}^{N}(y_{k}-t_{k})^{2}\qquad\qquad\qquad\qquad\ \ \ \ \ (6)$
$\newline$

$\boldsymbol{(a)}\ 训练隐层权值改变量$ $\newline$
$\qquad$按照链式求导法则： $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{ \partial w_{jk} } &= \dfrac{\partial E}{\partial y_{k}} \dfrac{\partial y_{k}}{\partial \beta_{k}} \dfrac{\partial \beta_{k}}{\partial w_{jk}} \\ &= (y_{k}-t_{k}) \dfrac{\partial y_{k}}{\partial \beta_{k}} \dfrac{\partial \beta_{k}}{\partial w_{jk}} \qquad\qquad 由\beta_{k}=\displaystyle\sum_{j=0}^{M}a_{j}w_{jk} \\ &= (y_{k}-t_{k}) \dfrac{\partial y_{k}}{\partial \beta_{k}} a_{j} \end{aligned} \newline$
$\qquad$考虑分类问题，输出层的激活函数 $h(\cdot)$采用 $softmax$函数，即 $y_{k}=h(\beta_{k})=\dfrac{e^{\beta_{k}}}{\sum_{n=1}^{N}e^{\beta_{n}}}$。 $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial y_{k}}{\partial \beta_{k}} &= \left( \dfrac{e^{\beta_{k}}}{ e^{\beta_{1}}+\cdots+e^{\beta_{k}}+\cdots+e^{\beta_{N}}} \right)^{'} \\ &= \dfrac{e^{\beta_{k}}\left( e^{\beta_{1}}+\cdots+e^{\beta_{k}}+\cdots+e^{\beta_{N}} \right)-e^{\beta_{k}}e^{\beta_{k}}}{\left( e^{\beta_{1}}+\cdots+e^{\beta_{k}}+\cdots+e^{\beta_{N}} \right)^{2}} \\ &=\dfrac{e^{\beta_{k}}}{ e^{\beta_{1}}+\cdots+e^{\beta_{k}}+\cdots+e^{\beta_{N}} } \cdot \dfrac{\left(e^{\beta_{1}}+\cdots+e^{\beta_{k}}+\cdots+e^{\beta_{N}} \right)-e^{\beta_{k}}}{ e^{\beta_{1}}+\cdots+e^{\beta_{k}}+\cdots+e^{\beta_{N}} } \\ &=y_{k}(1-y_{k}) \end{aligned} \newline$

$\qquad$因此，可求得： $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{\partial w_{jk} }=(y_{k}-t_{k}) \dfrac{\partial y_{k}}{\partial \beta_{k}} a_{j} =(y_{k}-t_{k})y_{k}(1-y_{k})a_{j} \qquad\qquad\qquad(7) \end{aligned} \newline$

$\boldsymbol{(b)}\ 训练输入层权值改变量$ $\newline$
$\qquad$由于训练误差可写为 $\newline$
$\qquad\qquad$ $\begin{aligned} E &=\dfrac{1}{2}\displaystyle\sum_{k=1}^{N}(y_{k}-t_{k})^{2} \\ &=\dfrac{1}{2}(y_{1}-t_{1})^{2}+\cdots+\dfrac{1}{2}(y_{k}-t_{k})^{2}+\cdots+\dfrac{1}{2}(y_{N}-t_{N})^{2} \end{aligned} \newline$

$\qquad$其中，每个 $y_{k}=h(\beta_{k})=h\left( \displaystyle\sum_{j=0}^{M}a_{j}w_{jk} \right)\ ,\ k=1,2,\cdots,N$ 中都含有 $a_{j}$ 。
$\qquad$因此， $\ \ \ \dfrac{\partial y_{k}}{\partial a_{j}} = \dfrac{\partial y_{k}}{\partial \beta_{k}}\dfrac{\partial \beta_{k}} {\partial a_{j}} = y_{k}(1-y_{k})w_{jk} \newline$

$\qquad$按照链式求导法则：

$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{ \partial v_{ij} } &= \dfrac{\partial E}{\partial y_{1}} \dfrac{\partial y_{1}}{\partial a_{j}} \dfrac{\partial a_{j}}{\partial \alpha_{j}} \dfrac{\partial \alpha_{j}}{\partial v_{jk}} + \cdots + \dfrac{\partial E}{\partial y_{k}} \dfrac{\partial y_{k}}{\partial a_{j}} \dfrac{\partial a_{j}}{\partial \alpha_{j}} \dfrac{\partial \alpha_{j}}{\partial v_{jk}} + \cdots + \dfrac{\partial E}{\partial y_{N}} \dfrac{\partial y_{N}}{\partial a_{j}} \dfrac{\partial a_{j}}{\partial \alpha_{j}} \dfrac{\partial \alpha_{j}}{\partial v_{jk}}\\ &= \sum\limits_{k=1}^{N} \dfrac{\partial E}{\partial y_{k}} \dfrac{\partial y_{k}}{\partial a_{j}} \dfrac{\partial a_{j}}{\partial \alpha_{j}} \dfrac{\partial \alpha_{j}}{\partial v_{jk}} \\ &= \sum\limits_{k=1}^{N}(y_{k}-t_{k}) y_{k}(1-y_{k})w_{jk} \dfrac{\partial a_{j}}{\partial \alpha_{j}} \dfrac{\partial \alpha_{j}}{\partial v_{jk}} \qquad\qquad 由\alpha_{j}=\displaystyle\sum_{i=0}^{L} x_{i} v_{ij} \\ &= \sum\limits_{k=1}^{N}(y_{k}-t_{k}) y_{k}(1-y_{k})w_{jk}\dfrac{\partial a_{j}}{\partial \alpha_{j}} x_{i} \end{aligned} \newline$

$\qquad$隐层的激活函数 $g(\cdot)$采用 $sigmoid$函数，即 $a_{j}=g(\alpha_{j})=\dfrac{1}{1+e^{-\alpha_{j}}}$。 $\newline$

$\qquad\qquad$ $\begin{aligned} \dfrac{\partial a_{j}}{\partial \alpha_{j}} &= \left(\dfrac{1}{1+e^{-\alpha_{j}}} \right)^{'} \\ &= \dfrac{-e^{-\alpha_{j}}(-1)}{\left(1+e^{-\alpha_{j}} \right)^{2}} \\ &= \dfrac{e^{-\alpha_{j}}}{\left(1+e^{-\alpha_{j}} \right)^{2}} \\ &=\dfrac{1}{1+e^{-\alpha_{j}}} \cdot \dfrac{e^{-\alpha_{j}}}{1+e^{-\alpha_{j}}} \\ &=a_{j}(1-a_{j}) \end{aligned} \newline$

$\qquad$因此
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{ \partial v_{ij} } &= \sum\limits_{k=1}^{N} \dfrac{\partial E}{\partial y_{k}} \dfrac{\partial y_{k}}{\partial a_{j}} \dfrac{\partial a_{j}}{\partial \alpha_{j}} \dfrac{\partial \alpha_{j}}{\partial v_{jk}} \\ &= \sum\limits_{k=1}^{N}(y_{k}-t_{k}) y_{k}(1-y_{k})w_{jk}\dfrac{\partial a_{j}}{\partial \alpha_{j}} x_{i} \\ &= \sum\limits_{k=1}^{N}(y_{k}-t_{k}) y_{k}(1-y_{k})w_{jk} a_{j}(1-a_{j}) x_{i} \qquad\qquad\qquad(8) \end{aligned} \newline$

$\qquad$为了方便表示，记 $\newline$
$\qquad\qquad$ $\delta_{o}(k) = (y_{k}-t_{k})y_{k}(1-y_{k})\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ (9)\newline$
$\qquad\qquad$ $\delta_{h}(j) = a_{j}(1-a_{j})\sum\limits_{k=1}^{N} \delta_{o}(k)w_{jk}\qquad\qquad\qquad\qquad\qquad\qquad\ \ \ (10) \newline$
$\qquad$公式 $(7)、(8)$分别可以改写为： $\newline$
$\qquad\qquad$ $\dfrac{\partial E}{\partial w_{jk} }=(y_{k}-t_{k})y_{k}(1-y_{k})a_{j}=\delta_{o}(k)a_{j} \newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{ \partial v_{ij} } &= \sum\limits_{k=1}^{N}(y_{k}-t_{k}) y_{k}(1-y_{k})w_{jk} a_{j}(1-a_{j}) x_{i} \\ &=\delta_{h}(j) x_{i} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \ \ \ \ (11) \end{aligned} \newline$
$\qquad$隐层权值的更新公式 $(4)$、输入层权值的更新公式 $(5)$分别可以改写为： $\newline$
$\qquad\qquad$ $w_{jk}=w_{jk}-\eta \dfrac{\partial E}{\partial w_{jk}}=w_{jk}-\eta\delta_{o}(k)a_{j}\qquad\qquad\qquad\qquad\qquad(12) \newline$
$\qquad\qquad$ $v_{ij}=v_{ij}-\eta \dfrac{\partial E}{\partial v_{ij}}=v_{ij}-\eta\delta_{h}(j) x_{i} \qquad\qquad\qquad\qquad\qquad\ \ \ \ \ \ (13) \newline$

$\qquad$总结：在 $sequential$模式下，令训练数据集 $\{\boldsymbol{x}^{(p)},\boldsymbol{t}^{(p)}\}_{p=1}^{P}$中的每一个数据 $\{\boldsymbol{x},\boldsymbol{t}\}=\{\boldsymbol{x}^{(p)},\boldsymbol{t}^{(p)}\}$按照一定的顺序、依次进入到多层感知器。 $\newline$
$\qquad$其训练过程如以下步骤： $\newline$
$\qquad1)$ 输入一个新的训练数据 $\{\boldsymbol{x},\boldsymbol{t}\}=\{\boldsymbol{x}^{(p)},\boldsymbol{t}^{(p)}\}，p=1$，按照 $2.4$ 的步骤，即公式 $(3)$，计算多层感知器的输出值 $\boldsymbol{y}=\boldsymbol{y}^{(p)}\left(对应2.3矩阵的第\ p\ 行\right)$ ，产生的训练误差即由公式 $(6)$计算 $\newline$
$\qquad2)$ 计算公式 $(9)$，得到 $\delta_{o}(1),\delta_{o}(2),\cdots,\delta_{o}(N)$ $\newline$
$\qquad3)$ 计算公式 $(12)$，更新所有的隐层权值 $w_{jk}$ $\newline$
$\qquad4)$ 计算公式 $(10)$，得到 $\delta_{h}(1),\delta_{h}(2),\cdots,\delta_{h}(M)$ $\newline$
$\qquad5)$ 计算公式 $(13)$，更新所有的输入层权值 $v_{ij}$ $\newline$
$\qquad6)$ 回到第一步，令 $p=p+1$，重新开始更新权值，直到 $p=P$ 时结束训练 $\newline$

$\boldsymbol{3.2}\ \ \ batch$ 模式 $\newline$
$\qquad$每次进入一批训练数据（假设为 $P$ 个），前向传播得到输出值之后，再通过误差反向传递来训练所有权值 $\left(\boldsymbol{v},\boldsymbol{w}\right)$。
$\qquad$假设 $P$ 个训练数据为 $\{\boldsymbol{x}^{(p)},\boldsymbol{t}^{(p)}\}_{p=1}^{P}$，第 $p$ 个输入数据为 $\boldsymbol{x}^{(p)}=(x_{1}^{(p)},\cdot\cdot\cdot,x_{L}^{(p)},-1)$， $\boldsymbol{t}^{(p)}=(t_{1}^{(p)},t_{2}^{(p)},\cdot\cdot\cdot,t_{N}^{(p)})$，通过多层感知器之后的输出为 $\boldsymbol{y}^{(p)}=(y_{1}^{(p)},y_{2}^{(p)},\cdot\cdot\cdot,y_{N}^{(p)})$
$\qquad$训练这一批数据所产生的平均误差为：
$\qquad\qquad E=\dfrac{1}{2P}\displaystyle\sum_{p=1}^{P}\left( \displaystyle\sum_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)})^{2}\right) \qquad\qquad\qquad\qquad(14)$
$\newline$

$\boldsymbol{(a)}\ 训练隐层权值改变量$ $\newline$

$\qquad$一批数据所产生的平均误差又可写为： $\newline$
$\qquad\qquad$ $\begin{aligned} E&=\dfrac{1}{2P}\displaystyle\sum_{p=1}^{P}\left( \displaystyle\sum_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)})^{2}\right) \\ &= \dfrac{1}{2P} \displaystyle\sum_{k=1}^{N}(y_{k}^{(1)}-t_{k}^{(1)})^{2}+\cdots+\dfrac{1}{2P} \displaystyle\sum_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)})^{2}+\cdots+\dfrac{1}{2P} \displaystyle\sum_{k=1}^{N}(y_{k}^{(P)}-t_{k}^{(P)})^{2} \\ \end{aligned} \newline$

$\qquad$显然，任何一个输入训练数据 $\boldsymbol{x}^{(p)}$ 的输出 $\boldsymbol{y}^{(p)}$ 都对 $\frac{\partial E}{ \partial w_{jk} }$ 有贡献。 $\newline$

$\qquad$按照链式求导法则： $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{ \partial w_{jk} } &= \dfrac{\partial E}{\partial y_{k}^{(1)}} \dfrac{\partial y_{k}^{(1)}}{\partial \beta_{k}^{(1)}} \dfrac{\partial \beta_{k}^{(1)}}{\partial w_{jk}} +\cdots+ \dfrac{\partial E}{\partial y_{k}^{(p)}} \dfrac{\partial y_{k}^{(p)}}{\partial \beta_{k}^{(p)}} \dfrac{\partial \beta_{k}^{(p)}}{\partial w_{jk}} + \cdots + \dfrac{\partial E}{\partial y_{k}^{(P)}} \dfrac{\partial y_{k}^{(P)}}{\partial \beta_{k}^{(P)}} \dfrac{\partial \beta_{k}^{(P)}}{\partial w_{jk}} \\ &= \displaystyle\sum_{p=1}^{P} \left[ \dfrac{\partial E}{\partial y_{k}^{(p)}} \dfrac{\partial y_{k}^{(p)}}{\partial \beta_{k}^{(p)}} \dfrac{\partial \beta_{k}^{(p)}}{\partial w_{jk}} \right] \qquad\qquad\qquad\ \ 由y^{(p)}=h(\beta_{k}^{(p)})=h\left(\displaystyle\sum_{j=0}^{M}a_{j}^{(p)}w_{jk} \right) \\ &=\dfrac{1}{P} \displaystyle\sum_{p=1}^{P} \left[ (y_{k}^{(p)} -t_{k}^{(p)}) \dfrac{\partial y_{k}^{(p)}}{\partial \beta_{k}^{(p)}} \dfrac{\partial \beta_{k}^{(p)}}{\partial w_{jk}} \right] \qquad\ \ \ 由\beta_{k}^{(p)}=\displaystyle\sum_{j=0}^{M}a_{j}^{(p)}w_{jk} \\ &=\dfrac{1}{P} \displaystyle\sum_{p=1}^{P} \left[ (y_{k}^{(p)} -t_{k}^{(p)}) \dfrac{\partial y_{k}^{(p)}}{\partial \beta_{k}^{(p)}} a_{j}^{(p)} \right] \end{aligned} \newline$
$\qquad$考虑分类问题，输出层的激活函 $h(\cdot)$采用 $softmax$函数，即 $y_{k}^{(p)}=h(\beta_{k}^{(p)})=\dfrac{e^{\beta_{k}^{(p)}}}{\sum_{n=1}^{N}e^{\beta_{n}^{(p)}}}$。由 $sequential$ 模式的结论，则有： $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial y_{k}^{(p)}}{\partial \beta_{k}^{(p)}} &=y_{k}^{(p)}(1-y_{k}^{(p)}) \end{aligned} \newline$

$\qquad$因此，可求得： $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{\partial w_{jk} }=\dfrac{1}{P}\displaystyle\sum_{p=1}^{P} \left[ (y_{k}^{(p)} -t_{k}^{(p)}) \dfrac{\partial y_{k}^{(p)}}{\partial \beta_{k}^{(p)}} a_{j}^{(p)} \right] = \dfrac{1}{P}\displaystyle\sum_{p=1}^{P} \left[ (y_{k}^{(p)} -t_{k}^{(p)}) y_{k}^{(p)}(1-y_{k}^{(p)}) a_{j}^{(p)} \right] \qquad(15) \end{aligned} \newline$

$\boldsymbol{(b)}\ 训练输入层权值改变量$ $\newline$
$\qquad$由于训练误差可写为 $\newline$
$\qquad\qquad$ $\begin{aligned} E&=\dfrac{1}{2P}\displaystyle\sum_{p=1}^{P}\left( \displaystyle\sum_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)})^{2}\right) \\ &= \dfrac{1}{2P} \displaystyle\sum_{k=1}^{N}(y_{k}^{(1)}-t_{k}^{(1)})^{2}+\cdots+\dfrac{1}{2P} \displaystyle\sum_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)})^{2}+\cdots+\dfrac{1}{2P} \displaystyle\sum_{k=1}^{N}(y_{k}^{(P)}-t_{k}^{(P)})^{2} \\ \end{aligned} \newline$
$\qquad$对于其中任何一个训练数据 $\{\boldsymbol{x}^{(p)},\boldsymbol{t}^{(p)}\}$，可以直接套用 $sequential$ 模式的结论： $\newline$
$\qquad\qquad$ $\begin{aligned} E^{(p)} &=\dfrac{1}{2P}\displaystyle\sum_{k=1}^{N}(y_{k}^{(p)} -t_{k}^{(p)})^{2} \\ &=\dfrac{1}{2P}(y_{1}^{(p)}-t_{1}^{(p)})^{2}+\cdots+\dfrac{1}{2P}(y_{k}^{(p)}-t_{k}^{(p)})^{2}+\cdots+\dfrac{1}{2P}(y_{N}^{(p)}-t_{N}^{(p)})^{2} \end{aligned} \newline$

$\qquad$其中，每个 $y_{k}^{(p)}=h(\beta_{k}^{(p)})=h\left( \displaystyle\sum_{j=0}^{M}a_{j}^{(p)} w_{jk} \right)\ ,\ k=1,2,\cdots,N$ 中都含有 $a_{j}^{(p)}$ 。
$\qquad$因此， $\ \ \ \dfrac{\partial y_{k}^{(p)}}{\partial a_{j}^{(p)}} = \dfrac{\partial y_{k}^{(p)}}{\partial \beta_{k}^{(p)}}\dfrac{\partial \beta_{k}^{(p)}} {\partial a_{j}^{(p)}} = y_{k}^{(p)}(1-y_{k}^{(p)})w_{jk} \newline$

$\qquad$按照链式求导法则： $\newline$

$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E^{(p)}}{ \partial v_{ij} } &= \dfrac{\partial E^{(p)}}{\partial y_{1}^{(p)}} \dfrac{\partial y_{1}^{(p)}}{\partial a_{j}^{(p)}} \dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} \dfrac{\partial \alpha_{j}^{(p)}}{\partial v_{jk}} + \cdots + \dfrac{\partial E^{(p)}}{\partial y_{k}^{(p)}} \dfrac{\partial y_{k}^{(p)}}{\partial a_{j}^{(p)}} \dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} \dfrac{\partial \alpha_{j}^{(p)}}{\partial v_{jk}} + \cdots \\ &\qquad + \dfrac{\partial E^{(p)}}{\partial y_{N}^{(p)}} \dfrac{\partial y_{N}^{(p)}}{\partial a_{j}^{(p)}} \dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} \dfrac{\partial \alpha_{j}^{(p)}}{\partial v_{jk}}\\ &= \sum\limits_{k=1}^{N} \dfrac{\partial E^{(p)}}{\partial y_{k}^{(p)}} \dfrac{\partial y_{k}^{(p)}}{\partial a_{j}^{(p)}} \dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} \dfrac{\partial \alpha_{j}^{(p)}}{\partial v_{jk}} \qquad\ \ \ \ \ \ \ \ 由a_{j}^{(p)}=g(\alpha_{j}^{(p)})=g\left(\displaystyle\sum_{i=0}^{L} x_{i}^{(p)} v_{ij}\right) \\ &= \dfrac{1}{P}\sum\limits_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)}) y_{k}^{(p)}(1-y_{k}^{(p)})w_{jk} \dfrac{\partial a_{j}}{\partial \alpha_{j}} \dfrac{\partial \alpha_{j}}{\partial v_{jk}} \\ &= \dfrac{1}{P}\sum\limits_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)}) y_{k}^{(p)}(1-y_{k}^{(p)})w_{jk}\dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} x_{i}^{(p)} \end{aligned} \newline$

$\qquad$隐层的激活函数 $g(\cdot)$采用 $sigmoid$函数，即 $a_{j}^{(p)}=g(\alpha_{j}^{(p)})=\dfrac{1}{1+e^{-\alpha_{j}^{(p)}}}$。 $\newline$

$\qquad\qquad$ $\begin{aligned} \dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} =a_{j}^{(p)}(1-a_{j}^{(p)}) \end{aligned} \newline$

$\qquad$因此
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E^{(p)}}{ \partial v_{ij} } &= \sum\limits_{k=1}^{N} \dfrac{\partial E^{(p)}}{\partial y_{k}^{(p)}} \dfrac{\partial y_{k}^{(p)}}{\partial a_{j}^{(p)}} \dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} \dfrac{\partial \alpha_{j}^{(p)}}{\partial v_{jk}} \\ &= \dfrac{1}{P}\sum\limits_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)}) y_{k}^{(p)}(1-y_{k}^{(p)})w_{jk}\dfrac{\partial a_{j}^{(p)}}{\partial \alpha_{j}^{(p)}} x_{i}^{(p)} \\ &= \dfrac{1}{P}\sum\limits_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)}) y_{k}^{(p)}(1-y_{k}^{(p)})w_{jk} a_{j}^{(p)}(1-a_{j}^{(p)}) x_{i}^{(p)} \qquad\ \ \ (16) \end{aligned} \newline$

$\qquad$为了方便表示，记 $\newline$
$\qquad\qquad$ $\delta_{o}^{(p)}(k) = \dfrac{1}{P}(y_{k}^{(p)}-t_{k}^{(p)})y_{k}^{(p)}(1-y_{k}^{(p)})\qquad\qquad\qquad\qquad\qquad\qquad\ \ \ \ (17)\newline$
$\qquad\qquad$ $\begin{aligned} \delta_{h}^{(p)}(j) &= a_{j}^{(p)}(1-a_{j}^{(p)}) \sum\limits_{k=1}^{N} \delta_{o}^{(p)}(k)w_{jk} \qquad\qquad\qquad\qquad\qquad\ \ \ \ \ \ \ \ \ \ \ (18) \end{aligned} \newline$

$\qquad$公式 $(15)$ 可以改写为： $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{\partial w_{jk} }&= \sum\limits_{p=1}^{P} \dfrac{\partial E^{(p)}}{\partial w_{jk} } \\ &=\dfrac{1}{P}\sum\limits_{p=1}^{P}(y_{k}^{(p)}-t_{k}^{(p)})y_{k}^{(p)}(1-y_{k}^{(p)})a_{j}^{(p)} \\ &=\sum\limits_{p=1}^{P}\delta_{o}^{(p)}(k)a_{j}^{(p)} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \ \ \ \ \ \ \ \ \ (19) \end{aligned} \newline$
$\qquad$公式 $(16)$ 可以改写为： $\newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E^{(p)}}{ \partial v_{ij} } &= \dfrac{1}{P}\sum\limits_{k=1}^{N}(y_{k}^{(p)}-t_{k}^{(p)}) y_{k}^{(p)}(1-y_{k}^{(p)})w_{jk} a_{j}^{(p)}(1-a_{j}^{(p)}) x_{i}^{(p)} \\ &= a_{j}^{(p)}(1-a_{j}^{(p)}) \sum\limits_{k=1}^{N} \delta_{o}^{(p)}(k) w_{jk} x_{i}^{(p)} \\ &=\delta_{h}^{(p)}(j) x_{i}^{(p)} \end{aligned} \newline$
$\qquad\qquad$ $\begin{aligned} \dfrac{\partial E}{ \partial v_{ij} } = \sum\limits_{p=1}^{P}\dfrac{\partial E^{(p)}}{\partial v_{ij} } = \sum\limits_{p=1}^{P}\delta_{h}^{(p)}(j) x_{i}^{(p)} \qquad\qquad\qquad\qquad\qquad\qquad\ \ \ \ \ (20) \end{aligned} \newline$

$\qquad$隐层权值的更新公式 $(4)$、输入层权值的更新公式 $(5)$分别可以改写为： $\newline$
$\qquad\qquad$ $w_{jk}=w_{jk}-\eta \dfrac{\partial E}{\partial w_{jk}}=w_{jk}-\eta \displaystyle\sum_{p=1}^{P}\delta_{o}^{(p)}(k)a_{j}^{(p)}\qquad\qquad\qquad\qquad\ \ \ \ (21) \newline$
$\qquad\qquad$ $v_{ij}=v_{ij}-\eta \dfrac{\partial E}{\partial v_{ij}}=v_{ij}-\eta \displaystyle\sum_{p=1}^{P}\delta_{h}^{(p)}(j) x_{i}^{(p)} \qquad\qquad\qquad\qquad\qquad\ \ (22) \newline$

$\qquad$总结：在 $batch$模式下，其训练过程如以下步骤 $($可参考 $2.3$ 中介绍的矩阵表示 $)$： $\newline$
$\qquad1)$ 所有训练数据 $\{\boldsymbol{x}^{(p)},\boldsymbol{t}^{(p)}\}_{p=1}^{P}$ 按照一定的顺序、依次进入到多层感知器，按照 $2.4$ 的步骤，即公式 $(3)$，计算多层感知器的输出值 $\{\boldsymbol{y}^{(p)}\}_{p=1}^{P}$，数据集中所有的 $P$ 个数据所产生的平均训练误差即由公式 $(14)$计算 $\newline$
$\qquad2)$ 计算公式 $(17)$，得到 $\{\delta_{o}^{(p)}(k),k=1,2,\cdots,N \}_{p=1}^{P}$ $\newline$
$\qquad3)$ 计算公式 $(19),(21)$，更新所有的隐层权值 $w_{jk}$ $\newline$
$\qquad4)$ 计算公式 $(18)$，得到 $\{\delta_{h}^{(p)}(j),j=1,2,\cdots,M \}_{p=1}^{P}$ $\newline$
$\qquad5)$ 计算公式 $(20),(22)$，更新所有的输入层权值 $v_{ij}$ $\newline$
$\qquad6)$ 重复 $1)\sim5)$多次，比如采用 $early\ stopping$来确定重复的次数以结束训练 $\newline$

4. 算法实现

$\qquad$ 算法的python实现取自于Machine Learning - An Algorithmic Perspective(2nd Edition)一书的第4章，通过MNIST数据集进行了测试。
关键代码段如下：
1）输入数据通过多层感知器的前向传播

def mlpfwd(self,inputs):
        """ Run the network forward """

        self.hidden = np.dot(inputs,self.weights1);
        self.hidden = 1.0/(1.0+np.exp(-self.beta*self.hidden))
        self.hidden = np.concatenate((self.hidden,-np.ones((np.shape(inputs)[0],1))),axis=1)

        outputs = np.dot(self.hidden,self.weights2);

        # Different types of output neurons
        if self.outtype == 'linear':
        	return outputs
        elif self.outtype == 'logistic':
            return 1.0/(1.0+np.exp(-self.beta*outputs))
        elif self.outtype == 'softmax':
            normalisers = np.sum(np.exp(outputs),axis=1)*np.ones((1,np.shape(outputs)[0]))
            return np.transpose(np.transpose(np.exp(outputs))/normalisers)
        else:
            print "error"

2）batch模式下的误差反向传播训练所有权值(权值的更新采用了动量法)，weights1表示输入层权值，weights2表示隐层权值，分别对应了 $2.3$ 中的矩阵表示

    def mlptrain(self,inputs,targets,eta,niterations):
        """ Train the thing """    
        # Add the inputs that match the bias node
        inputs = np.concatenate((inputs,-np.ones((self.ndata,1))),axis=1)
        change = range(self.ndata)
    
        updatew1 = np.zeros((np.shape(self.weights1)))
        updatew2 = np.zeros((np.shape(self.weights2)))
            
        for n in range(niterations):
    
            self.outputs = self.mlpfwd(inputs)

            error = 0.5*np.sum((self.outputs-targets)**2)
            if (np.mod(n,100)==0):
                print "Iteration: ",n, " Error: ",error    

            # Different types of output neurons
            if self.outtype == 'linear':
            	deltao = (self.outputs-targets)/self.ndata
            elif self.outtype == 'softmax':
                deltao = (self.outputs-targets)*(self.outputs*(-self.outputs)+self.outputs)/self.ndata 
            else:
            	print "error"
            
            deltah = self.hidden*self.beta*(1.0-self.hidden)*(np.dot(deltao,np.transpose(self.weights2)))
                      
            updatew1 = eta*(np.dot(np.transpose(inputs),deltah[:,:-1])) + self.momentum*updatew1
            updatew2 = eta*(np.dot(np.transpose(self.hidden),deltao)) + self.momentum*updatew2
            self.weights1 -= updatew1
            self.weights2 -= updatew2

3）early stopping方式确定batch模式的重复训练次数（默认重复训练100次为一个基本步骤）

    def earlystopping(self,inputs,targets,valid,validtargets,eta,niterations=100):
    
        valid = np.concatenate((valid,-np.ones((np.shape(valid)[0],1))),axis=1)
        
        old_val_error1 = 100002
        old_val_error2 = 100001
        new_val_error = 100000
        
        count = 0
        while (((old_val_error1 - new_val_error) > 0.001) or ((old_val_error2 - old_val_error1)>0.001)):
            count+=1
            print count
            self.mlptrain(inputs,targets,eta,niterations)
            old_val_error2 = old_val_error1
            old_val_error1 = new_val_error
            validout = self.mlpfwd(valid)
            new_val_error = 0.5*np.sum((validtargets-validout)**2)
            
        print "Stopped", new_val_error,old_val_error1, old_val_error2
        return new_val_error

初始化过程：

    def __init__(self,inputs,targets,nhidden,beta=1,momentum=0.9,outtype='logistic'):
        """ Constructor """
        # Set up network size
        self.nin = np.shape(inputs)[1]
        self.nout = np.shape(targets)[1]
        self.ndata = np.shape(inputs)[0]
        self.nhidden = nhidden

        self.beta = beta
        self.momentum = momentum
        self.outtype = outtype
    
        # Initialise network
        self.weights1 = (np.random.rand(self.nin+1,self.nhidden)-0.5)*2/np.sqrt(self.nin)
        self.weights2 = (np.random.rand(self.nhidden+1,self.nout)-0.5)*2/np.sqrt(self.nhidden)

主程序1——batch模式：

import pylab as pl
import numpy as np
import mlp
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

nread = 10000                     # 读取10000个训练数据
# Just use the first few images
train_in = x_train[:nread,:]
train_tgt = np.zeros((nread,10))
for i in range(nread):
    train_tgt[i,t_train[i]] = 1
    
# Make sure you understand how it does it
test_in = x_test[:10000,:]       # 读取10000个测试数据
test_tgt = np.zeros((10000,10))
for i in range(nread):
    test_tgt[i,t_test[i]] = 1
    
# We will need the validation set
valid_in = x_train[nread:nread*2,:]   # 读取10000个验证数据(用于early stopping)
valid_tgt = np.zeros((nread,10))
for i in range(nread):
    valid_tgt[i,t_train[nread+i]] = 1

for i in [20,50]:                   # 隐层节点数分别为20和50
    print "----- "+str(i)  
    net = mlp.mlp(train_in,train_tgt,i,outtype='softmax')
    net.earlystopping(train_in,train_tgt,valid_in,valid_tgt,0.1)
    net.confmat(test_in,test_tgt)

测试结果：
----- 20个隐层节点
1
Iteration: 0 Error: 4548.353637882863
2
Iteration: 0 Error: 1487.0759421425435
3
Iteration: 0 Error: 896.5361419007859
4
Iteration: 0 Error: 677.5059512878594
5
Iteration: 0 Error: 573.3650508668917
6
Iteration: 0 Error: 494.1811634917851
… …
12
Iteration: 0 Error: 403.34490704933353
13
Iteration: 0 Error: 397.1756959426855
… …
30
Iteration: 0 Error: 354.4125339850196
31
Iteration: 0 Error: 353.305132917339
32
Iteration: 0 Error: 366.55628156059623
33
Iteration: 0 Error: 350.1651292612425
Stopped 857.3212342735881 857.0808281664059 854.2069505493689
Percentage Correct: 88.97 （识别率）
----- 50个隐层节点
1
Iteration: 0 Error: 4575.487855803707
2
Iteration: 0 Error: 733.3021704371301
3
Iteration: 0 Error: 501.26273959844514
4
Iteration: 0 Error: 438.9892263452885
5
Iteration: 0 Error: 405.4943514143844
6
Iteration: 0 Error: 385.16563035185777
… …
16
Iteration: 0 Error: 300.94481634009423
17
Iteration: 0 Error: 296.32368821391657
… …
49
Iteration: 0 Error: 214.4658877695538
50
Iteration: 0 Error: 213.05563233179032
Stopped 698.1289903467069 697.9241528560016 697.6666825463668
Percentage Correct: 91.36（识别率）

主程序2 —— mini batch模式（训练集和验证集的选取可以随意选择）：

import pylab as pl
import numpy as np
import mlp
from dataset.mnist import load_mnist

# Read the dataset in (code from sheet)
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

nread = 5000           # 确定mini batch的批处理数据集中的数据量，此处为5000个数据作为一组
test_in = x_test[:,:]
test_tgt = np.zeros((10000,10))  #测试集为10000个数据
for i in range(10000):
    test_tgt[i,t_test[i]] = 1
      
ntimes = 60000/nread   # 60000个训练集可以分成12组，第n组为训练集时，第n+1组为验证集
for n in range(ntimes):    
    print n
    # training set 训练集
    train_in = x_train[nread*n:nread*(n+1),:]
    train_tgt = np.zeros((nread,10))
    for i in range(nread):
        train_tgt[i,t_train[nread*n+i]] = 1
        
    # validation set 验证集   
    valid_tgt = np.zeros((nread,10)) 
    if n < ntimes-1:           
        valid_in = x_train[nread*(n+1):nread*(n+2),:]
        for i in range(nread):  
            valid_tgt[i,t_train[nread*(n+1)+i]] = 1  
    else:
        valid_in = x_train[0:nread,:]
        for i in range(nread):  
            valid_tgt[i,t_train[i]] = 1
        
    if n==0:
        net = mlp.mlp(train_in,train_tgt,40,outtype='softmax')  #40个隐层节点
        
    net.earlystopping(train_in,train_tgt,valid_in,valid_tgt,0.1)
    net.confmat(test_in,test_tgt)

测试结果：（识别率逐步提高）
0
Percentage Correct: 88.66000000000001
1
Percentage Correct: 90.36
2
Percentage Correct: 90.86999999999999
3
Percentage Correct: 91.36
4
Percentage Correct: 91.67
5
Percentage Correct: 91.85
6
Percentage Correct: 92.46
7
Percentage Correct: 92.38
8
Percentage Correct: 92.75999999999999
9
Percentage Correct: 93.06
10
Percentage Correct: 93.07
11
Percentage Correct: 92.85

（有待检查）