阴阳
题面
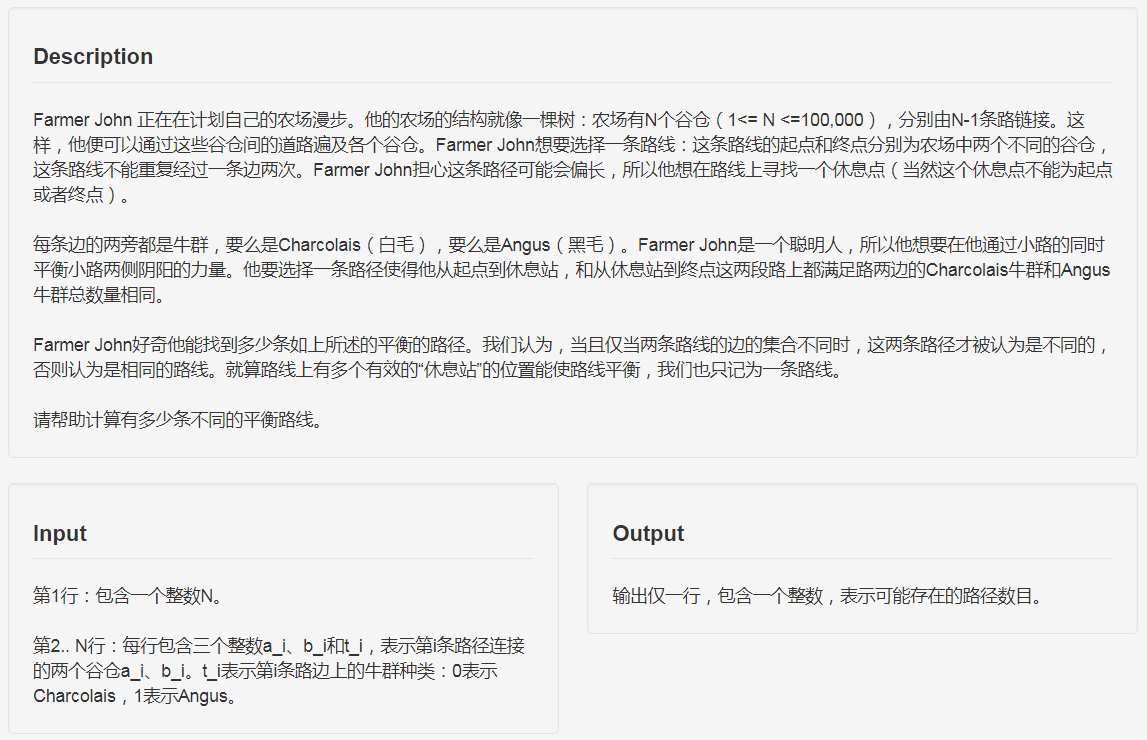
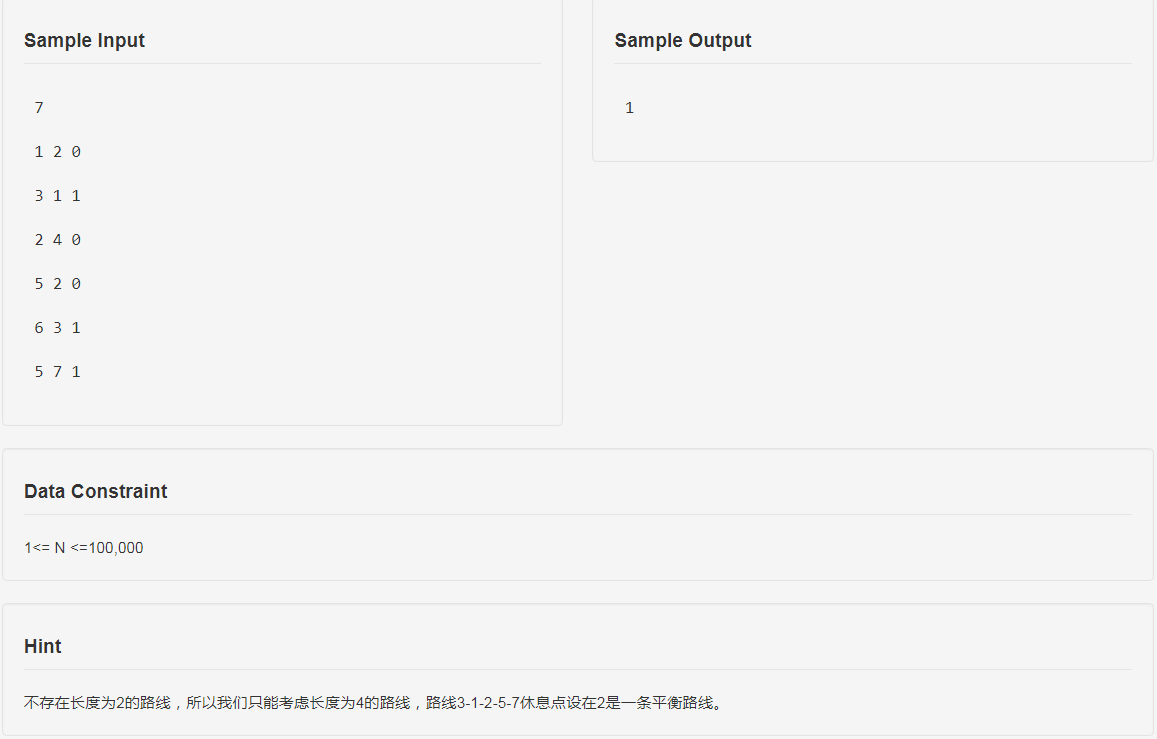
分析
个人认为是极好的题,很容易写
如果你学点分治是无奈背板的,那就做做这道题,加深你对点分治的理解
一般的,处理树上大规模统计问题,我们分治的关键是找一棵子树的重心
找到分治中心,即新一轮的根节点,然后处理子树节点经过根节点时的答案,接着对子树继续分治下去
那么我们看这题,让黑白的各自变为 \(1\) 或 \(-1\)
合法的路径是这样的:能找到一个分割点使路径两端各自的和分别为 \(0\)
那么我们思考在统计经过根节点的答案时,只有不同子树的两路径合并时或一棵子树中某节点到根距离为 \(0\) 且其路径上有分割点才可能产生答案
也就是说,我们要找的路径和必须为 \(0\) 且有分割点
找路径和为 \(0\) 很简单,记录子树节点到根的距离 \(dis\)(可能为负,所以让他加上 \(n\) 避免出错),两路径合并时,设其两端为 \(x,y\),\(dis[x]+dis[y] = 0\) 是必要条件
重点就是如何判断两路径是否有分割点,是的话我们就可以统计答案
那么我们回到 \(dis[x]+dis[y] = 0\) 这句话
\(dis[y]=-dis[x]\),若 \(dis[y]\) 他到根节点中 值是非第一次出现的,那么可以直接贡献答案
我们只需要记下这类点的个数就好了,即开桶以值为下标记个数,我们称其为二类桶
???那一类桶呢?
既然二类桶是非第一次出现,那一类桶就记第一次出现的个数
我们可以用 \(flag[x]=1\) 表示 \(dis[x]\) 已经出现过
因为是遍历子树是深搜的顺序,所以我们再开个桶标记在他到根节点路径中 \(dis\) 出现的次数,这样就可以很好的判断 \(flag\) 是否需要标记为 \(1\)
那么考虑当前节点如何计算答案
- 若他的 \(dis\) 到根节点是第一次出现,那么他可以直接加上二类桶。注意 \(dis\) 为 \(0\) 的话他又可以加一类桶,因为此时的根可以为路径的分割点
- 若他的 \(dis\) 到根节点不是第一次出现,那么他可以加上一、二类桶,因为他先前的 \(dis\) 到他的距离为 \(0\),即先前的 \(dis\) 可做分割点。当然,此时他 \(dis\) 若为 \(0\) 同理说明他到根也是合法路径,所以答案加 \(1\)。记得标记当前点的 \(flag\) 为 \(1\)
每次统计完一个子树,就要再遍历一遍这个子树更新一类、二类桶的信息
换重心时我们不能直接把数组清 \(0\),为了保证复杂度,我们统计完所有子树的答案后再遍历一遍所有子树,将一类、二类桶的信息退回,\(flag\) 和 \(dis\) 清 \(0\)
完结撒花
\(Code\)
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 5;
int n , buc[N << 1] , buc1[N << 1][3] , flag[N] , dis[N] , h[N] , size , siz[N] , son[N] , rt , use[N] , tot;
LL ans;
struct edge{
int to , nxt , w;
}e[2 * N];
inline void add(int x , int y , int z)
{
e[++tot].nxt = h[x];
e[tot].to = y;
e[tot].w = z;
h[x] = tot;
}
inline void getrt(int x , int fa)
{
son[x] = 0 , siz[x] = 1;
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == fa || use[v]) continue;
getrt(v , x);
siz[x] += siz[v];
son[x] = max(son[x] , siz[v]);
}
son[x] = max(son[x] , size - siz[x]);
rt = son[x] < son[rt] ? x : rt;
}
inline void getdis(int x , int fa)
{
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == fa || use[v]) continue;
dis[v] = dis[x] + e[i].w;
getdis(v , x);
}
}
inline void fill(int x , int fa)
{
++buc1[dis[x] + n][flag[x]];
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == fa || use[v]) continue;
fill(v , x);
}
}
inline void clear(int x , int fa)
{
--buc1[dis[x] + n][flag[x]];
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == fa || use[v]) continue;
clear(v , x);
}
dis[x] = flag[x] = 0;
}
inline LL dfs(int x , int fa)
{
LL res = 0;
if (buc[dis[x] + n]) flag[x] = 1 , res += buc1[-dis[x] + n][0] + buc1[-dis[x] + n][1] + (!dis[x] ? 1 : 0);
else{
if (!dis[x]) res += buc1[-dis[x] + n][0];
res += buc1[-dis[x] + n][1];
}
++buc[dis[x] + n];
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == fa || use[v]) continue;
res += dfs(v , x);
}
--buc[dis[x] + n];
return res;
}
inline LL calc(int x)
{
getdis(x , 0);
LL res = 0;
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (use[v]) continue;
res += dfs(v , x);
fill(v , x);
}
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (use[v]) continue;
clear(v , x);
}
return res;
}
inline void divide(int x)
{
use[x] = 1 , ans += calc(x);
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
if (use[v]) continue;
size = siz[v] , rt = 0;
getrt(v , x) , divide(rt);
}
}
int main()
{
scanf("%d" , &n);
int u , v , w;
for(register int i = 1; i < n; i++)
{
scanf("%d%d%d" , &u , &v , &w);
w = w ? 1 : -1;
add(u , v , w) , add(v , u , w);
}
son[0] = 2e9 , size = n;
getrt(1 , 0) , divide(rt);
printf("%lld" , ans);
}