T1: 序章-弗兰德的秘密
首先熟悉一下同构的定义:
1、两棵树节点个数相等。
2、两棵树的以根节点的儿子为根子树对应同构。如下图,为两 棵同构的有根树。
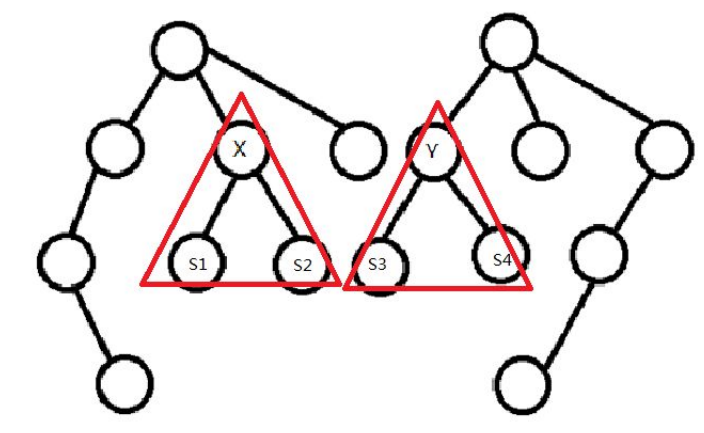
看复杂度,我们一般会想到用$O(N^2)$的算法吧。
那么,考虑树形DP。
设 $f_{i,j}$表示两棵树分别以$i, j$为根时的最大同构值。
那么,我们要想得到$f_{i,j}$,肯定要先得知其儿子。那么,如上图,对于$x,y$来讲,$f_{x,y} = max( f_{sonx, sony} ) + 1$
于是,我们对于树$1$每个点,对应枚举树$2$每个点,同时枚举双方儿子进行转移。
总复杂度: $O(5!N^2)$
#include <bits/stdc++.h> using namespace std; #define N 1010 inline int read(){ int x = 0 ,s = 1; char c = getchar(); while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); } while(isdigit(c)){ x = x * 10 + (c ^ '0'); c = getchar(); } return x * s; } vector <int> G[N]; vector <int> T[N]; int f[N][N], x, y; // f[x][y]: x、y作为根节点的最大同构数 int vis[N]; int n, m; void dfs1(int best, int step){ // 上一层最优解 + 已搜儿子个数 if(step > G[x].size()){ f[x][y] = max(f[x][y], best); return ; } dfs1(best, step + 1); bool judge = 0; for(int i = 0; i < T[y].size(); i++){ if(!vis[i]){ vis[i] = 1; judge = 1; dfs1(best + f[G[x][step - 1]][T[y][i]], step + 1); vis[i] = 0; } } if(!judge) f[x][y] = max(f[x][y], best); // 递归下去有最优解时不用更新 return ; } void dfs(int now){ if(G[now].size() == 0){ // 第一棵树无儿子, 只有自己 for(int i = 1;i <= m; i++) f[now][i] = 1; return ; } for(int i = 0; i < G[now].size(); i++) dfs(G[now][i]); for(int i = 1; i <= m; i++){ if(T[i].size() == 0) f[now][i] = 1; // 检查第二棵树是否有儿子 else { x = now, y = i; dfs1(0, 1); f[now][i]++; } } return ; } int main(){ // freopen("frand.in", "r", stdin); // freopen("frand.out", "w", stdout); n = read(), m = read(); for(int i = 1;i < n; i++){ int x = read(), y = read(); G[x].push_back(y); } for(int i = 1; i < m; i++){ int x = read(), y = read(); T[x].push_back(y); } dfs(1); printf("%d\n", f[1][1]); return 0; }
T2:圣章-精灵使的魔法语
中二的题目水了一大堆,其实就是让我们求一个区间内括号的失配数和一个单点修改。
于是考虑线段树,维护$tag1$:该区间左括号失配树。$tag2$: 该区间右括号失配数。
那么,我们在合并时,有:
t[o].tag1 = t[o << 1 | 1].tag1 + max(t[o << 1].tag1 - t[o << 1 | 1].tag2, 0); t[o].tag2 = t[o << 1].tag2 + max(t[o << 1 | 1].tag2 - t[o << 1].tag1, 0);
在查询区间失配数时,考虑用指针上传区间合并答案。
#include <bits/stdc++.h> using namespace std; #define N 160000 inline int read(){ int x = 0, s = 1; char c = getchar(); while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); } while(isdigit(c)){ x = x * 10 + (c ^ '0'); c = getchar(); } return x * s; } struct tree{ int tag1, tag2; } t[N << 2]; int ans1, ans2; int a[N]; void pushup(int o){ t[o].tag1 = t[o << 1 | 1].tag1 + max(t[o << 1].tag1 - t[o << 1 | 1].tag2, 0); t[o].tag2 = t[o << 1].tag2 + max(t[o << 1 | 1].tag2 - t[o << 1].tag1, 0); return ; } void build(int o, int l, int r){ if(l == r){ if(a[l] == '(') t[o].tag1 = 1; else t[o].tag2 = 1; return ; } int mid = l + r >> 1; build(o << 1, l, mid); build(o << 1 | 1, mid + 1, r); pushup(o); return ; } void update(int o, int l, int r, int x){ if(l > x || r < x) return ; if(l == r && l == x){ t[o].tag1 ^= 1; t[o].tag2 ^= 1; // printf("o: %d tag1: %d tag2: %d\n", o, t[o].tag1, t[o].tag2); return ; } int mid = l + r >> 1; update(o << 1, l, mid, x); update(o << 1 | 1, mid + 1, r, x); pushup(o); // printf("o: %d tag1: %d tag2: %d\n", o, t[o].tag1, t[o].tag2); return ; } void query(int o, int l, int r, int in, int end, int& lk, int& rk){ if(l > end || r < in) { lk = 0, rk = 0; // 千万不要忘了 lk = 0, rk = 0 return ; } if(l >= in && r <= end){ lk = t[o].tag1; rk = t[o].tag2; return ; } int mid = l + r >> 1; int lsum, rsum, lsum1, rsum1; query(o << 1, l, mid, in, end, lsum, rsum); // 获得左边括号 query(o << 1 | 1, mid + 1, r, in, end, lsum1, rsum1); // 获得右边括号 lk = lsum1 + max(lsum - rsum1, 0); // 合并 rk = rsum + max(rsum1 - lsum, 0); return ; } int main(){ // freopen("hh.txt", "r", stdin); // freopen("lk10.in", "r", stdin); // freopen("lk10.out","w", stdout); int n = read(), m = read(); for(int i = 1;i <= n; i++){ char c; cin >> c; a[i] = (int)c; } build(1, 1, n); char s[20]; while(m--){ scanf("%s", s); if(s[0] == 'Q'){ int x = read(), y = read(); ans1 = 0, ans2 = 0; query(1, 1, n, x, y, ans1, ans2); printf("%d %d\n", ans2, ans1); } else { int x = read(); update(1, 1, n, x); } } return 0; }
T3:终章-剑之魂
40pts: 双重循环枚举即可(送分)
100pts: 对于 and 操作,我们想要的肯定是二进制下尽可能1的位数较高。
那么,我们考虑从二进制高位往低位枚举。
对于我们目前的一个最优$ans$,一个数能和它 & 上,则这个数必须能保证$a_i$ & $ans = ans$ 如果不能,代表这个数的前面数位太小,不能使得$ans$最大。舍去。
其次,如何保证我们的 $ans$可以在这一位填上$1$呢? 很好想: 如果有大于等于两个数可以在满足条件一(前面的数位最大)的情况下,这一位又都有1,那么我们就可以在这一位填上1了。
总复杂度: $O(30 * N)$
#include <bits/stdc++.h> using namespace std; #define N 5000010 inline int read(){ int x = 0, s = 1; char c = getchar(); while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); } while(isdigit(c)){ x = x * 10 + (c ^ '0'); c = getchar(); } return x * s; } int a[N]; long long ans = 0; int main(){ // freopen("sword.in","r", stdin); // freopen("sword.out", "w", stdout); int n = read(); for(int i = 1;i <= n; i++) a[i] = read(); for(int i = 30; i >= 0; i--){ int num = 0; for(int j = 1;j <= n; j++){ if((a[j] & ans) == ans && (a[j] & (1 << i)) == (1 << i)) num++; if(num >= 2) break; } if(num >= 2) ans += (1 << i); } cout << ans << endl; return 0; }