写作时间:2020-07-16
目录:
1.推荐一本书
2.开始第一课
3.总结一下
正文
1.推荐一本书
推荐一本书,《Numerical Computing with MATLAB》。
这本书是MATLAB 创始人 Clever B.Moler 编写。
该书强调 数学理论 基础,MATLAB作为工具,两者结合。
MATLAB官网上有该书英文版pdf、代码、小工具。
声明:
以下绝大部分内容来源于该书,只选取部分内容,整理学习,文章结构安排并非按照原文。
翻译参考了张老师的中译本内容。
强烈推荐看原著或者中译本。
2.lesson1-黄金分割比
2.1 黄金分割比的来历

大的矩形和小的矩形相似。
当然还有另一种表示方式:一维线段的表示方式。
即就是 :
1/x=(x-1)/1;
x^2-x-1=0
求解:
p(x)=x^2-x-1
2.2 使用MATLAB计算黄金分割比的N种方法
方法1
%方法1:
p=[1,-1,-1];
% 代表 p(x)=x^2-x-1
x=roots(p)
%结果如下---------------------------
% x =
%
% -0.6180
% 1.6180
方法2
%方法2:
syms x
r=solve(1/x == x-1);
%结果如下---------------------------
% r =
% 1/2 - 5^(1/2)/2
% 5^(1/2)/2 + 1/2
方法3
%方法3:
syms x
r=solve(1/x == x-1);
pretty(r)
%结果如下---------------------------
% / 1 sqrt(5) \
% | - - ------- |
% | 2 2 |
% | |
% | sqrt(5) 1 |
% | ------- + - |
% \ 2 2 /
更高精度显示
phi=r(1);
vpa(phi,50)
%结果如下---------------------------
%ans =
%-0.61803398874989484820458683436563811772030917980576
double(phi)
%结果如下---------------------------
%ans =
%ans =
% -0.6180
方法4
f=@ (x)1./x-(x-1);%利用匿名函数,f是函数句柄
f
fplot(f,[0.1,4]);
phi=fzero(f,1);
hold on;
grid on;
plot(phi,0,'o');
运行结果:
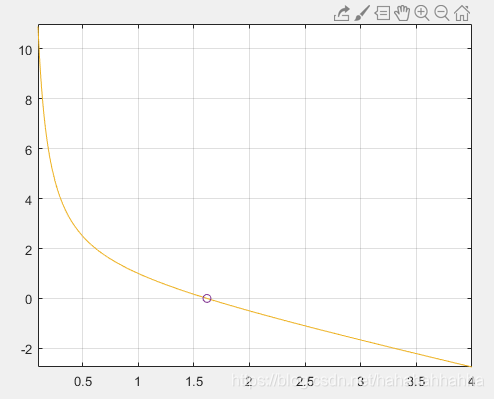
绘制黄金分割矩形
phi =(1+sqrt(5))/2;
%绘制矩形依次的点x(k),y(k),注意是5个点,要回到第一个点
x=[0 phi phi 0 0];
y=[0 0 1 1 0];
%依次的点u(k),v(k)
u=[1 1];
v=[0 1];
plot(x,y,'b.-',u,v,'b.--');
text(phi/2,1.05,'\phi');
text((1+phi)/2,-0.05,'\phi-1');
text(-0.05,0.5,'1');
text(0.5,-0.05,'1');
axis equal;
axis off;
set(gcf,'color','white');
运行结果:

方法5:
利用一个迭代(套娃)公式,这是另一种全新的方法!!!
迭代就像套娃一样。
该(套娃)公式如下:
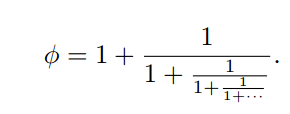

代码如下:
clc
n=6;
%使用迭代次数为6逼近最终值
%n越大越好
%第1段code
p='1';
for k=1:n
p=['1+1/(' p ')'];
end
p
%第2段code
p=1;
q=1;
for k=1:n
temp=p;%先保护好原来的p,放在temp暂存
p=p+q;%赋值改变p,p=p+q
q=temp;%q赋值为原来的p
disp([p,q]);
end
p=sprintf("%d/%d",p,q)
%第3段code
format long
p=eval(p)
format short
err=(1+sqrt(5)/2)-p
%结果如下---------------------------
% p =
%
% '1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1))))))'
%
% 2 1
%
% 3 2
%
% 5 3
%
% 8 5
%
% 13 8
%
% 21 13
%
%
% p =
%
% "21/13"
%
%
% p =
%
% 1.615384615384615
%
%
% err =
%
% 0.5026
第1段和第3段,好理解,不赘述。
第2段代码,看不懂,好难,解释如下:
表达式左边可改写如右边。
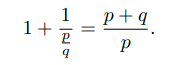
把
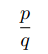
看成迭代(套娃,洋葱)里面的一层。
把
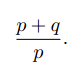
看成迭代(套娃,洋葱)外边的一层。
那么就是,使用
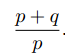
不断的迭代
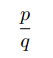
。
迭代的初始赋值为:
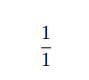
现在理解了第2段代码了。
多说一句:
这就是为什么说高手用迭代递归,关于迭代(套娃、洋葱)这里,我之前写过一文,有兴趣可以阅读。
汉诺塔游戏程序可以通过“迭代递归”来实现?但你未必清楚其根本原因。
*再发散一下:
方法5第2段代码输出如下:
%
% 2 1
%
% 3 2
%
% 5 3
%
% 8 5
%
% 13 8
%
% 21 13
咦,这不就是斐波那契数列(兔子数列) ,那是因为迭代的过程中,我们使用p=p+q;q=p;
3.总结一下
无。
THE END~