非线性SVM-重要参数kernel

非线性SVM的决策函数：

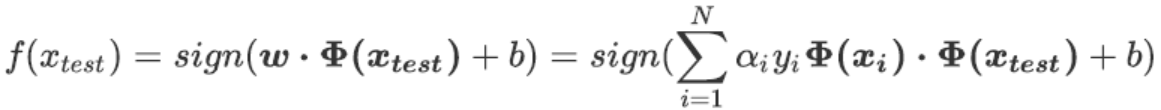
将数据从原始的空间投射到新空间中，这种变换非常巧妙，但也带有一些实现问题。
首先，我们可能不清楚应该什么样的数据应该使用什么类型的映射函数来确保可以在变换空间中找出线性决策边界。极端情况下，数据可能会被映射到无限维度的空间中，这种高维空间可能不是那么友好，维度越多，推导和计算的难度都会随之暴增。其次，即使已知适当的映射函数，我们想要计算类似于 $\Phi(x_i)\cdot\Phi(x_{test})$这样的点积，计算量可能会无比巨大，要找出超平面所付出的代价是非常昂贵的。
为了解决上述问题，我们引入了一个关键概念——核函数(Kernel Function)。解决上述问题的数学方式，叫做**“核技巧”(Kernel Trick)，是一种能够使用数据原始空间中的向量计算来表示升维后的空间中的点积结果的数学方式**。具体表现为 $K(u,v)=\Phi(u)\cdot\Phi(v)$ 。而这个原始空间中的点积函数K(u,v)，就被叫做“核函数”。
核函数能够帮助我们解决三个问题：
第一，有了核函数之后，我们无需去担心 $\Phi$究竟应该是什么样，因为非线性SVM中的核函数都是正定核函数(positive definite kernel functions)，他们都满足美世定律(Mercer’s theorem)，确保了高维空间中任意两个向量的点积一定可以被低维空间中的这两个向量的某种计算来表示（多数时候是点积的某种变换）。
第二，使用核函数计算低维度中的向量关系比计算原本的 $\Phi(x_i)\cdot\Phi(x_{test})$要简单太多了。
第三，因为计算是在原始空间中进行，所以避免了维度诅咒的问题。
选用不同的核函数，就可以解决不同数据分布下的寻找超平面问题。在SVC中，这个功能由参数“kernel”和一系列与核函数相关的参数来进行控制。之前的代码中我们一直使用这个参数并输入"linear"，但却没有给大家详细讲解，也是因为如果不先理解核函数本身，很难说明这个参数到底在做什么。参数“kernel"在sklearn中可选以下几种选项：

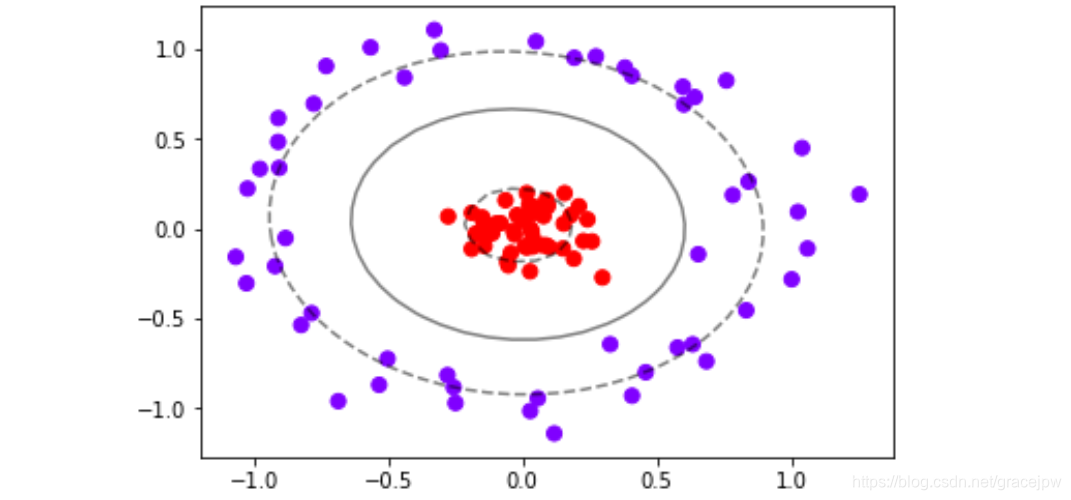
可以看出，除了选项"linear"之外，其他核函数都可以处理非线性问题。多项式核函数有次数d，当d为1的时候它就是在处理线性问题，当d为更高次项的时候它就是在处理非线性问题。我们之前画图时使用的是选项“linear"，自然不能处理环形数据这样非线性的状况。而刚才我们使用的计算r的方法，其实是高斯径向基核函数所对应的功能，在参数”kernel“中输入”rbf“就可以使用这种核函数。我们来看看模型找出的决策边界时什么样：

clf = SVC(kernel = "rbf").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)

可以看到，决策边界被完美地找了出来。