统计机器学习【3】- K近邻法（一）：基础知识

k近邻法是一种基本分类与回归算法。k近邻法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。是一种监督学习。

一、k近邻算法

输入：训练数据集
$\tau = \lbrace(x_1, y_1), (x_2, y_2), ..., (x_N, y_N) \rbrace$
其中， $x_i \in \chi \subseteq R^n为实例的特征向量， y_i \in \gamma = \lbrace c_1, c_2, ..., c_k \rbrace$ 为实例的类别， $i = 1, 2, ..., N$ ；实例特征向量 $x$ :
输出：实例 $x$ 所属的类 $y$

（1）根据给定的距离度量，在训练集 $T$ 中找出与 $x$ 最近邻的k个点，涵盖这 $k$ 个点的 $x$ 的邻域记作 $N_K(x)$ :

（2）在 $N_K(x)$ 中根据分类决策规则（如多数表决）决定 $x$ 的类别 $y$ :
$y = argmax_{\epsilon j} \sum_{x_i \in N_k(x)} I(y_i = c_j), i = 1, 2, ..., N; j = 1, 2,..., K \tag{1}$

式（1）中， $I$ 是指示函数，即当 $y_i = c_j$ 时 $I$ 为1，否则 $I$ 为0.

二、k近邻模型

k近邻法使用的模型实际上对应于特征空间的划分，模型由三个基本要素——距离度量、k值的选择和分类决策规则决定

（1）距离度量

特征空间中两个实例点的距离是两个实例点相似程度的反映，k近邻模型的特征空间一般是n维实数向量空间 $R^n$ 。使用的距离是欧式距离，但也可以是其它距离。
设特征空间 $\chi$ 是n维实数向量空间 $R^n$ ， $x_i, x_j \in \chi, x_i = (x_i^{(1)}, x_i^{(2)}, ..., x_i^{(n)})^T, x_j = (x_j^{(1)}, x_j^{(2)}, ..., x_j^{(n)})^T$ ， $x_i, x_j的L_p$ 距离定义为
$L_P(x_i, x_j) = (\sum_{l = 1}^n |x_i^{(l)} - x_j^{(l)}|^p)^{\frac{1}{p}}\tag{2}$

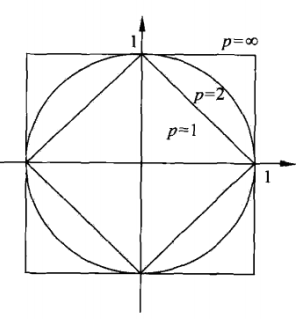
这里 $p \geq 1$ 。当 $p = 2$ 时，称为欧式距离，即
$L_2(x_i, x_j) = (\sum_{l=1}^n |x_i^{(l)} - x_j^{(j)}|^2)^{\frac{1}{2}} \tag{3}$ .

当 $p = 1$ 时，称为曼哈顿距离，即
$L_1(x_i, x_j) = \sum_{l = 1}^{n} |x_i^{(l)} - x_j^{(l)}| \tag{4}$

当 $p = \infty$ 时，它是各个坐标距离的最大值，即
$L_\infty (x_i, x_j) = max_l |x_i^{(l)} - x_j^{(l)}| \tag {5}$

在这里插入图片描述

（2）k值的选择

k值的选择会对k近邻法的结果产生重大影响。

较小的k值 -》》学习的近似误差减少，但学习的估计误差增大，预测结果会对近邻的实例敏感，如果临近的实例点恰是噪声，预测会出错，k值的减少意味着整体模型变复杂，容易发生过拟合
较大的k值 -》》学习的估计误差较少，但近似误差增大，与输入实例较远的训练实例也会对预测起作用，预测会发生错误，k值的增大就意味着整体模型变得简单

在应用中，k值一般取一个比较小的数值，通常采用交叉验证法来选取最优的k值。
同时我也在其它得资料中，看到有其他的选取k值的方法：首先计算训练集合中元素个数n求 $\sqrt n$ ,而且这个n最好是奇数。

（3）分类决策规则

k近邻法中的分类决策规则往往是多数表决，即由输入实例的k个近邻的训练实例中的多数类决定输入实例的类。

多数表决规则（majority voting relu）有如下解释：如果分类的损失函数为0-1损失函数，分类函数为
$f: R^n \rightarrow \{ c_1, c_2, ..., c_k\}$

那么误分类的概率是：
$P(Y \ne1 f(X)) = 1 - P(Y = f(X))$

对给定的实例 $x \in \chi，其最近邻的k个训练实例点构成集合$ N_k(x) $，如果涵盖$ N_k(x) $的区域的类别为$ c_j$，那么误分类率是：
$\frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i \neq c_j) = 1 - \frac{1}{k} \sum_{x_i \in N_k(x) }I(y_i = c_j)$
要使误分类率最小即经验风险最小，就要使 $\sum_{x_i \in N_k(x)}I(y_i = c_j)$ 最大，所有多数表决规则等价于经验风险最小化。

参考文献：
【1】统计学习方法——李航
【2】KNN Algorithm - How KNN Algorithm Works With Example | Data Science For Beginners | Simplilearn