Computer Graphics note(2):视图变换&投影变换

前提

Games101 lecture4-lecture5
考虑将三位物体转换二维图像需要的步骤，我们需要以下变换来达成目的，
model transformation(模型(基础)变换--Object就位)
view/camera transformation(视图变换--调整相机)
projection transformation(投影变换--变换到\([-1,1]^3\),忽略深度信息\(z\),变成\([-1,1]^2\))
viewport transformation(视口变换--投影到屏幕空间)
如下图所示(Fundamentals of Computer Graphics (3rd Edition) 7.1 Viewing Transformations Figure 7.2)：

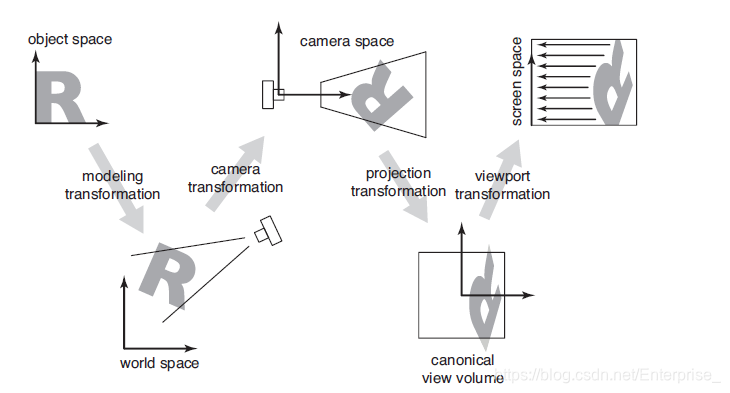
视图变换

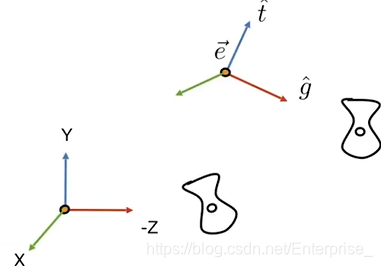
​ 首先需要定义一个相机，一个相机有三个属性，位置(Positon)\(\pmb{e}\)，观测方向(Look-at/ gaze direction)\(\pmb{g}\)和向上方向(Up direction)\(\pmb{t}\)。
​ 同时只要相机和物体之间没有相对运动，观测结果就不会改变，则可以让相机固定在原点，向上方向为\(Y\)方向，看向\(-Z\)方向，而这就需要通过变换矩阵\(M_view\)来自达成(需要注意的是物体也会随着相机移动而移动，因为要保证两者之间没有相对运动)，该矩阵需要完成如下操作:

1. 将原来在任意点\(\pmb{e}\)的相机平移到原点
2. 将观测方向\(\pmb{g}\)旋转到\(-Z\)方向
3. 将向上方向\(\pmb{t}\)旋转到\(Y\)方向
4. 将{\(\pmb{g}\)X\(\pmb{t}\)}方向旋转到\(X\)方向(当前两个方向旋转完成之后，\(X\)方向自然对齐)
   如下图所示:

\(M_{view}\)先平移在旋转(和仿射变换不同)，即\(M_{view}=R_{view}T_{view}\)。
最后结果如下:

\[M_{view}=R_{view}T_{view}=\begin{bmatrix} x_{gXt} &y_{gXt}&z_{gXt}&0\\ x_t&y_t&z_t&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} 1&0&0& -x_e\\ 0&1&0& -y_e\\ 0&0&1& -z_e\\ 0&0&0& 1\end{bmatrix} \]

推导过程

首先是平移到原点，可以很自然的写出其平移矩阵\(T_view\)如下:

\[T_view=\begin{bmatrix} 1&0&0& -x_e\\ 0&1&0& -y_e\\ 0&0&1& -z_e\\ 0&0&0& 1\end{bmatrix} \]

接着考虑旋转，将任意方向旋转到\(X,Y,-Z\)方向上不容易写出，但是可以考虑其逆变换，写出将\(X(1,0,0),Y(0,1,0),Z(0,0,1)\)旋转到{\(\pmb{g}\)X\(\pmb{t}\)},\(\pmb{t}\),\(\pmb{-g}\)的旋转矩阵\(R_{view}^{-1}\),并且由于旋转矩阵是正交矩阵，所以只要写出\(R_{view}^{-1}\)，其转置矩阵即为所求,如下所示：

\[R_{view}^{-1}=\begin{bmatrix} x_{gXt} &x_t&x_{-g}&0\\ y_{gXt} &y_t&y_{-g}&0\\ z_{gXt} &z_t&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} \]

可以通过将上述矩阵应用与三轴来检验其正确性。\(R_{view}\)如下所示:

\[R_{view} = R_{view}^{(-1)(-1)}=R_{view}^T= \begin{bmatrix} x_{gXt} &y_{gXt}&z_{gXt}&0\\ x_t&y_t&z_t&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} \]

所以最终的\(M_{view}\)如开头所示。

投影变换

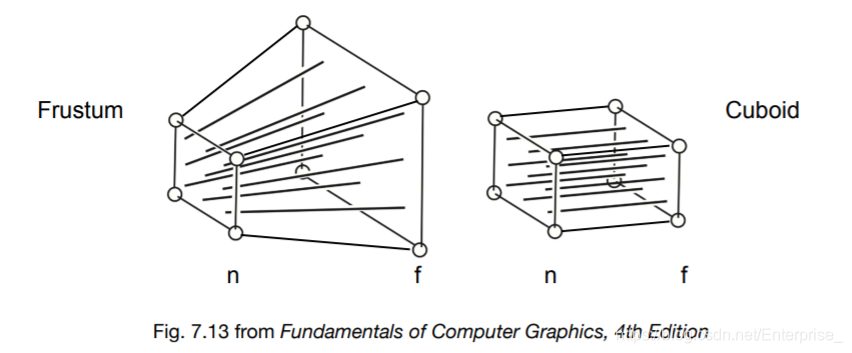
投影变换目的就是将物体变换到\([-1,1]^3\)。想要得到二维图像，可以去掉\(z\)，变成\([-1,1]^2\)。变换分为两种，正交(orthographic)投影和透视(prespective)投影。透视投影存在近大远小的现象，而正交投影则不会，这是两者的本质区别，两者分别如下图所示:
图片来源:https://stackoverflow.com/questions/36573283/from-perspective-picture-to-orthographic-picture

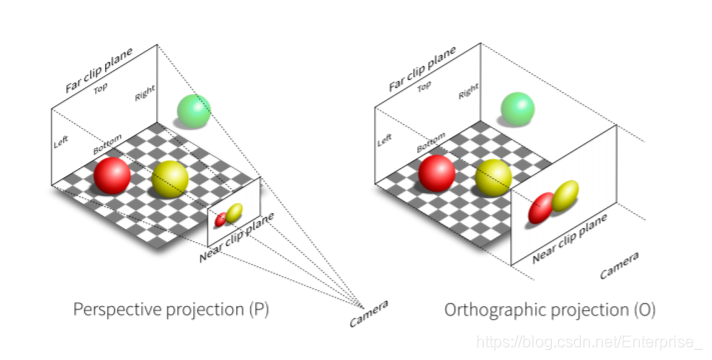
上图中透视投影围成一个视锥(四棱锥)，而视锥中从某一个深度到另一个深度之间的区域叫做\(frustum\),而透视投影就是将\(frustum\)中的东西显示到近平面(\(Near\) \(clip\) \(plane\))上。

正交投影(右手系)

首先定义一个空间中的立方体(只需定义6个面,左右上下前后)，\([l,r]\)x\([b,t]\)x\([f,n]\),需要注意的是远平面(\(f\))和近平面(\(n\))，有\(\pmb{n}>\pmb{f}\)因为看向\(-Z\)(右手系),所以物体越远则其对应的\(Z\)的值越小，反之越大。如果是左手系则越远\(Z\)越大，因为看向的\(+Z\)方向。然后将立方体中心平移到原点，并将其缩放成\(canonical\)(正则规范标准立方体) \(cube [-1,1]^3\),忽略\(z\),则变为\([-1,1]^2\)。
如下图所示：

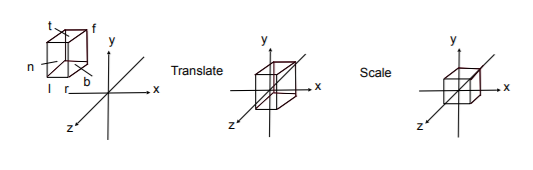
先将立方体中心\((\frac{r+l}{2},\frac{t+b}{2},\frac{n+f}{2})\)平移到原点，然后缩放到\([-1,1]^3\)(长宽高为\(2\))，这里的缩放其实就是将立方体的长宽高缩放为\(2\)，其变换矩阵\(M_{ortho}\)如下:

\[M_{ortho}=\begin{bmatrix} \frac{2}{r-l} &0&0&0\\ 0& \frac{2}{t-b} &0&0\\ 0&0& \frac{2}{n-f} &0\\ 0&0&0 &1 \end{bmatrix} \begin{bmatrix} 1&0&0& -\frac{r+l}{2}\\ 0&1&0& -\frac{t+b}{2}\\ 0&0&1& -\frac{n+f}{2}\\ 0&0&0& 1 \end{bmatrix}=\begin{bmatrix} \frac{2}{r-l}&0&0&-\frac{r+l}{r-l}\\ 0&\frac{2}{t-b}&0&-\frac{t+b}{t-b}\\ 0&0&\frac{2}{n-f}&-\frac{n+f}{n-f}\\ 0&0&0&1 \end{bmatrix} \]

透视投影

视锥定义

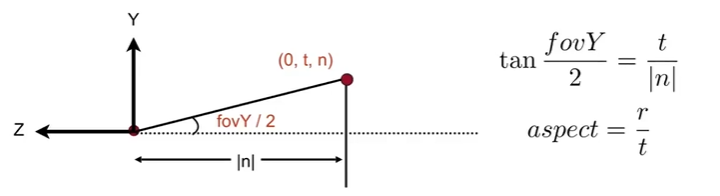
透视投影的视锥定义只要定义两个东西1.垂直可视角度$Y\(2.宽高比\)aspect$，如下图所示：

从侧面观察，则近平面距离相机距离为\(|n|\),如下图所示:

怎么做透视投影\(M_{persp}=M_{ortho}M_{persp->ortho}\)

1. 首先将\(frustum\)挤压成一个长方体(\(M_{persp->ortho}\))(\([l,r]\)x\([b,t]\)x\([f,n]\),)；
2. 然后再做一次正交投影(\(M_{ortho}\),已知)。即可完成投影到近平面的任务。

如下图所示:

前提规定

1. 在挤压过程(第一步)中\(frustum\)的近平面\(n\)上点不变；

2. \(f\)平面的\(Z\)值不变,因为只是在收缩；

3. \(f\)平面的中心点是不会改变的(挤压完还是中心点)。

推导过程

先单独考虑挤压过程，我们需要找到一个矩阵来完成变换。
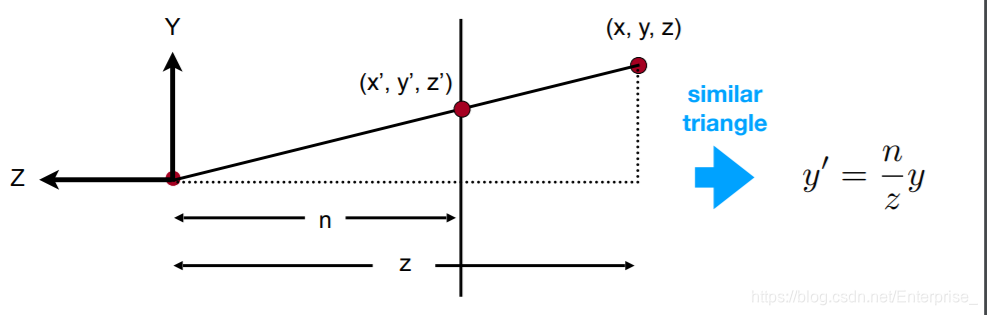
考虑下图，从视锥的侧面看，我们需要将\((x,y,z)\)挤压到和近平面上点\((x',y',z')\)一样的高度，考虑相似三角形，则有\(y'=\frac{n}{z}y\)；同理(从上面看)，对于\(x\)而言有\(x'=\frac{n}{z}x\)。

需要注意的是，这里\(\pmb{n},\pmb{z}\)在图上表示的是距离原点的距离(负\(Z\)方向)，所以是个负数。

至此，已知挤压过程\(x,y\)的变换，\(z\)未知，将上述变换用齐次坐标，同时在基础变换中我们提到过对于齐次坐标而言，\((x,y,z,w)^T(w!=0)\)表示的点即为\((\frac{x}{w},\frac{y}{w},\frac{z}{w},1)^T\)。 所以有如下关系:

\[M_{persp->ortho}\begin{bmatrix} x\\y\\z\\1 \end{bmatrix}=\begin{bmatrix} \frac{n}{z}x \\ \frac{n}{z}y \\ ? \\1 \end{bmatrix}\stackrel{同乘z}{=}\begin{bmatrix} nx\\ny\\?\\z \end{bmatrix} \]

从中可以反推出\(M_{persp->ortho}\)如下:

\[M_{persp->ortho}=\begin{bmatrix} n&0&0&0 \\ 0&n&0&0 \\ ?&?&?&? \\ 0&0&1&0 \end{bmatrix} \]

同时因为挤压过程中近平面点不变，远平面点\(Z\)值不变。则对于一个近平面上点\((x,y,n,1)^T\)(假设近平面上的\(z\)的值为\(n\))。考虑齐次坐标中一个点可以有很多不同的表示，同理则有\((x,y,n,1)^T\stackrel{同乘n}{=}(nx,ny,n^2,n)^T\)变换后是不变的。所以有如下关系:

\[M_{persp->ortho}\begin{bmatrix} x\\y\\n\\1 \end{bmatrix}=\begin{bmatrix} nx\\ny\\?\\z \end{bmatrix}=\begin{bmatrix} nx\\ny\\n^2\\n \end{bmatrix} \]

则可以推出变换矩阵的第三行为\((0,0,A,B)\),即有式子\((1)\)如下：

\[\begin{bmatrix} 0&0&A&B \end{bmatrix}\begin{bmatrix} x\\y\\n\\1 \end{bmatrix}=n^2\tag{1} \]

再考虑\(f\)平面中\(z\)不变，且中心点不变，则对于其中心点\((0,0,f,1)\)(假设远平面上\(z\)值为\(f\))。则有如下关系式子\((2)\):

\[\begin{bmatrix} 0\\0\\f\\1 \end{bmatrix}\stackrel{同乘f}{=}\begin{bmatrix} 0\\0\\f^2\\f \end{bmatrix}\Rightarrow\begin{bmatrix} 0&0&A&B \end{bmatrix}\begin{bmatrix} 0\\0\\f\\1 \end{bmatrix}=\begin{bmatrix} 0\\0\\f^2\\f \end{bmatrix}\tag{2} \]

由\((1)(2)\)可得，如下结果

\[\begin{cases} An+B=n^2\\ Af+B=f^2 \end{cases}\Rightarrow\begin{cases} A=n+f\\ B=-nf \end{cases} \]

则有

\[M_{persp->ortho}=\begin{bmatrix} n&0&0&0 \\ 0&n&0&0 \\ 0&0&n+f&-nf \\ 0&0&1&0 \end{bmatrix} \]

所以透视投影变换矩阵计算如下:

\[M_{persp}=M_{ortho}M_{persp->ortho}=\begin{bmatrix} \frac{2n}{r-l}&0&-\frac{r+l}{r-l}&0\\ 0&\frac{2n}{t-b}&-\frac{t+b}{t-b}&0\\ 0&0&\frac{n+f}{n-f}&-\frac{2nf}{n-f}\\ 0&0&1&0 \end{bmatrix} \]

Question:frustum中间的点的变化

在\(frustum\)中间任何一个位置，比如点\((x,y,\frac{n+f}{2},1)^T\)，经过挤压之后(不做第二步正交)更加靠近远平面还是近平面？(远平面)

推导过程

先将\(M_{persp->ortho}\)应用到该点上，如下：

\[M_{persp->ortho}\begin{bmatrix} x\\y\\\frac{n+f}{2}\\1 \end{bmatrix}=\begin{bmatrix} nx\\ny\\ \frac{(n+f)^2}{2}-nf\\ \frac{n+f}{2} \end{bmatrix}\stackrel{规范化，同除以\frac{n+f}{2}}{=}\begin{bmatrix} \frac{2nx}{n+f}\\ \frac{2ny}{n+f} \\ n+f-\frac{2nf}{n+f}\\1 \end{bmatrix} \]

比较变换前后两点的\(Z\)值大小，如下：

\[\begin{aligned} n+f-\frac{2nf}{n+f}-\frac{n+f}{2} &= \frac{n+f}{2}-\frac{2nf}{n+f} \\ &= \frac{(n+f)^2-4nf}{2(n+f)}\\ &= \frac{(n-f)^2}{2(n+f)} \end{aligned} \]

前面提到此时的\(n,f\)是个负数，所以有\((n-f)^2>0\)，\((n+f)<0\)，即更加靠近远平面。